Chào mừng các em học sinh đến với bộ đề trắc nghiệm Bài 2 môn Toán 6 Kết nối tri thức. Bài học này giúp các em nắm vững kiến thức về cách ghi số tự nhiên và hiểu rõ thứ tự trong tập hợp các số tự nhiên.
Với hình thức trắc nghiệm, các em sẽ được ôn luyện và củng cố kiến thức một cách nhanh chóng và hiệu quả. Hãy cùng giaitoan.edu.vn chinh phục bài học này nhé!
Cho n là một số tự nhiên lớn hơn 2 và nhỏ hơn 5. Khẳng định nào sau đây đúng?
n nằm bên phải điểm 5 trên tia số
n nằm bên trái điểm 2 trên tia số
n nằm bên phải điểm 2 trên tia số
n nằm bên phải điểm 5 và cách điểm 5 một đơn vị trên tia số.
\(\overline {a001} \left( {a \ne 0} \right)\) bằng
\(\overline {a001} = a \times 1000 + 0 \times 100 + 0 \times 10 + 1\)
\(\overline {a001} = 1000 + 0 \times 100 + 0 \times 10 + 1\)
\(\overline {a001} = a \times 1000 + 1 \times 100\)
\(\overline {a001} = a + 0 + 0 + 1\)
Viết số 24 bằng số La Mã
XXIIII
XXIX
XXIV
XIV
Số La Mã XXIV biểu diễn số nào trong hệ thập phân?
26
16
14
24
Năm 2000 là thế kỉ bao nhiêu?
XX
XIX
XXI
XXX
Số liền trước số \(1000\) là
\(1002\)
\(990\)
\(1001\)
\(999\)
Số tự nhiên liền sau số \(2018\) là
\(2016\)
\(2017\)
\(2019\)
\(2020\)
Thay a và b bằng một số tự nhiên phù hợp trong trường hợp sau:
17, b, a là ba số lẻ liên tiếp tăng dần.
\(a = 21,b = 19\)
\(a = 19,b = 21\)
\(a = 13,b = 15\)
\(a = 15,b = 13\)
Cho hai số tự nhiên \(99;100\). Hãy tìm số tự nhiên \(a\) để ba số có được tạo thành ba số tự nhiên liên tiếp.
\(98\)
\(97\)
\(101\)
Cả A, C đều đúng
Tìm các số tự nhiên \(a,b,c\) sao cho \(228 \le a < b < c \le 230.\)
\(a = 228;b = 229;c = 230\)
\(a = 227;b = 228;c = 229\)
\(a = 229;b = 230;c = 231\)
Không tồn tại \(a;b;c\) thỏa mãn đề bài.
Thêm chữ số \(7\) vào đằng trước số tự nhiên có ba chữ số thì ta được số tự nhiên mới
Hơn số tự nhiên cũ \(700\) đơn vị
Kém số tự nhiên cũ \(700\) đơn vị
Hơn số tự nhiên cũ \(7000\) đơn vị
Kém số tự nhiên cũ \(7000\) đơn vị
Với ba chữ số \(0;1;3\) có thể viết được bao nhiêu số có ba chữ số khác nhau?
\(4\)
\(3\)
\(5\)
\(6\)
Lời giải và đáp án
Cho n là một số tự nhiên lớn hơn 2 và nhỏ hơn 5. Khẳng định nào sau đây đúng?
n nằm bên phải điểm 5 trên tia số
n nằm bên trái điểm 2 trên tia số
n nằm bên phải điểm 2 trên tia số
n nằm bên phải điểm 5 và cách điểm 5 một đơn vị trên tia số.
Đáp án : C
+ Vẽ tia số.
+ Số tự nhiên lớn hơn thì nằm bên phải, nhỏ hơn thì nằm bên trái.
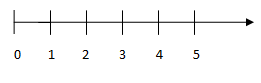
n là một số tự nhiên lớn hơn 2 nên n nằm bên phải điểm 2 => B sai, C đúng
n là một số tự nhiên nhỏ hơn 5 nên n nằm bên trái điểm 2 =>A,D sai.
\(\overline {a001} \left( {a \ne 0} \right)\) bằng
\(\overline {a001} = a \times 1000 + 0 \times 100 + 0 \times 10 + 1\)
\(\overline {a001} = 1000 + 0 \times 100 + 0 \times 10 + 1\)
\(\overline {a001} = a \times 1000 + 1 \times 100\)
\(\overline {a001} = a + 0 + 0 + 1\)
Đáp án : A
- Xác định hàng của từng chữ số trong mỗi số.
- Chữ số hàng đơn vị ta giữ nguyên
- Chữ số hàng chục nhân với 10.
- Chữ số hàng trăm nhân với 100.
- Chữ số hàng nghìn nhân với 1000.
Số a là chữ số hàng nghìn nên ta nhân với 1000.
Hai số 0 lần lượt là hàng trăm (nhân với 100) và hàng chục (nhân với 10).
Số 1 là chữ số hàng đơn vị (nhân với 1).
\(\overline {a001} = a \times 1000 + 0 \times 100 + 0 \times 10 + 1\).
Viết số 24 bằng số La Mã
XXIIII
XXIX
XXIV
XIV
Đáp án : C
- Số từ 21 đến 30 ta viết chữ XX trước.
- Nếu hàng đơn vị là các số từ 1 đến 9 thì ghép chữ số La Mã tương ứng với nó như trong bảng vào.

Chữ số 4 là IV
Ta thêm XX vào bên trái số IV thì được số 24: XXIV
Số La Mã XXIV biểu diễn số nào trong hệ thập phân?
26
16
14
24
Đáp án : D
- Bên trái của số La Mã có hai chữ số XX liên tiếp thì đó là số từ 20 đến 29.
- Các chữ số sau XX là một trong các số từ 1 đến 9 như trong bảng sau:

X có giá trị bằng 10
IV có giá trị bằng 4 nên số XXIV biểu diễn số 10+10+4=24
Năm 2000 là thế kỉ bao nhiêu?
XX
XIX
XXI
XXX
Đáp án : A
Cứ 100 năm là 1 thế kỉ.
Thế kỉ I bắt đầu từ ngày 1 tháng 1 năm 1 và kết thúc vào ngày 31 tháng 12 năm 100.
Năm cuối cùng của thế kỉ XX là 2000.
Năm 2000 là thế kỉ XX.
Số liền trước số \(1000\) là
\(1002\)
\(990\)
\(1001\)
\(999\)
Đáp án : D
+ Hai số tự nhiên liên tiếp hơn kém nhau 1 đơn vị
+ Số tự nhiên liền trước số \(a\) là số $a - 1.$
Số tự nhiên liền trước số \(1000\) là số \(1000 - 1 = 999.\)
Số tự nhiên liền sau số \(2018\) là
\(2016\)
\(2017\)
\(2019\)
\(2020\)
Đáp án : C
+ Hai số tự nhiên liên tiếp hơn kém nhau 1 đơn vị nên số tự nhiên liền sau hơn số tự nhiên liền trước nó là \(1\) đơn vị.
Số tự nhiên liền sau số \(2018\) là số \(2018 + 1 = 2019.\)
Thay a và b bằng một số tự nhiên phù hợp trong trường hợp sau:
17, b, a là ba số lẻ liên tiếp tăng dần.
\(a = 21,b = 19\)
\(a = 19,b = 21\)
\(a = 13,b = 15\)
\(a = 15,b = 13\)
Đáp án : A
Các số lẻ liên tiếp cách nhau 2 đơn vị
b là số lẻ liền sau 17, a là số lẻ liền sau b.
17, b, a là ba số lẻ liên tiếp tăng dần nên các số đó lần lượt là 17, 19, 21.
Vậy \(a = 21,b = 19\)
Cho hai số tự nhiên \(99;100\). Hãy tìm số tự nhiên \(a\) để ba số có được tạo thành ba số tự nhiên liên tiếp.
\(98\)
\(97\)
\(101\)
Cả A, C đều đúng
Đáp án : D
Sử dụng các số tự nhiên liên tiếp hơn kém nhau \(1\) đơn vị để tìm các số thích hợp
Số liền trước số \(99\) là \(98\) nên ba số tự nhiên liên tiếp là \(98;99;100\)
Số liền sau số \(100\) là \(101\) nên ba số tự nhiên liên tiếp là \(99;100;101\)
Vậy cả hai số \(98;101\) đều thỏa mãn yêu cầu đề bài.
Tìm các số tự nhiên \(a,b,c\) sao cho \(228 \le a < b < c \le 230.\)
\(a = 228;b = 229;c = 230\)
\(a = 227;b = 228;c = 229\)
\(a = 229;b = 230;c = 231\)
Không tồn tại \(a;b;c\) thỏa mãn đề bài.
Đáp án : A
Tìm các số tự nhiên thỏa mãn đề bài rồi sắp xếp theo thứ tự tăng dần để tìm \(a;b;c.\)
Từ đề bài, ta thấy các số tự nhiên lớn hơn hoặc bằng \(228\) và nhỏ hơn hoặc bằng \(230\) là
\(228;229;230.\)
Mà \(a < b < c\) nên ta có \(a = 228;b = 229;c = 230.\)
Thêm chữ số \(7\) vào đằng trước số tự nhiên có ba chữ số thì ta được số tự nhiên mới
Hơn số tự nhiên cũ \(700\) đơn vị
Kém số tự nhiên cũ \(700\) đơn vị
Hơn số tự nhiên cũ \(7000\) đơn vị
Kém số tự nhiên cũ \(7000\) đơn vị
Đáp án : C
Sử dụng mối quan hệ giữa các chữ số trong số tự nhiên.
Trong hệ thập phân, cứ mười đơn vị của một hàng thì làm thành đơn vị của hàng liền trước đó.
Gọi số có ba số ban đầu là \(\overline {abc} \) , viết thêm chữ số \(7\) vào đằng trước ta được \(\overline {7abc} \) .
Ta có \(\overline {7abc} = 7000 + \overline {abc} \) nên số mới hơn số cũ \(7000\) đơn vị.
Với ba chữ số \(0;1;3\) có thể viết được bao nhiêu số có ba chữ số khác nhau?
\(4\)
\(3\)
\(5\)
\(6\)
Đáp án : A
- Ta viết các số tự nhiên có ba chữ số khác nhau lập thành từ ba số \(0;1;3\) sao cho chữ số hằng trăm khác \(0\).
- Đếm các số.
Có bốn số tự nhiên thỏa mãn đề bài là \(310;301;103;130.\)
Cho n là một số tự nhiên lớn hơn 2 và nhỏ hơn 5. Khẳng định nào sau đây đúng?
n nằm bên phải điểm 5 trên tia số
n nằm bên trái điểm 2 trên tia số
n nằm bên phải điểm 2 trên tia số
n nằm bên phải điểm 5 và cách điểm 5 một đơn vị trên tia số.
\(\overline {a001} \left( {a \ne 0} \right)\) bằng
\(\overline {a001} = a \times 1000 + 0 \times 100 + 0 \times 10 + 1\)
\(\overline {a001} = 1000 + 0 \times 100 + 0 \times 10 + 1\)
\(\overline {a001} = a \times 1000 + 1 \times 100\)
\(\overline {a001} = a + 0 + 0 + 1\)
Viết số 24 bằng số La Mã
XXIIII
XXIX
XXIV
XIV
Số La Mã XXIV biểu diễn số nào trong hệ thập phân?
26
16
14
24
Năm 2000 là thế kỉ bao nhiêu?
XX
XIX
XXI
XXX
Số liền trước số \(1000\) là
\(1002\)
\(990\)
\(1001\)
\(999\)
Số tự nhiên liền sau số \(2018\) là
\(2016\)
\(2017\)
\(2019\)
\(2020\)
Thay a và b bằng một số tự nhiên phù hợp trong trường hợp sau:
17, b, a là ba số lẻ liên tiếp tăng dần.
\(a = 21,b = 19\)
\(a = 19,b = 21\)
\(a = 13,b = 15\)
\(a = 15,b = 13\)
Cho hai số tự nhiên \(99;100\). Hãy tìm số tự nhiên \(a\) để ba số có được tạo thành ba số tự nhiên liên tiếp.
\(98\)
\(97\)
\(101\)
Cả A, C đều đúng
Tìm các số tự nhiên \(a,b,c\) sao cho \(228 \le a < b < c \le 230.\)
\(a = 228;b = 229;c = 230\)
\(a = 227;b = 228;c = 229\)
\(a = 229;b = 230;c = 231\)
Không tồn tại \(a;b;c\) thỏa mãn đề bài.
Thêm chữ số \(7\) vào đằng trước số tự nhiên có ba chữ số thì ta được số tự nhiên mới
Hơn số tự nhiên cũ \(700\) đơn vị
Kém số tự nhiên cũ \(700\) đơn vị
Hơn số tự nhiên cũ \(7000\) đơn vị
Kém số tự nhiên cũ \(7000\) đơn vị
Với ba chữ số \(0;1;3\) có thể viết được bao nhiêu số có ba chữ số khác nhau?
\(4\)
\(3\)
\(5\)
\(6\)
Cho n là một số tự nhiên lớn hơn 2 và nhỏ hơn 5. Khẳng định nào sau đây đúng?
n nằm bên phải điểm 5 trên tia số
n nằm bên trái điểm 2 trên tia số
n nằm bên phải điểm 2 trên tia số
n nằm bên phải điểm 5 và cách điểm 5 một đơn vị trên tia số.
Đáp án : C
+ Vẽ tia số.
+ Số tự nhiên lớn hơn thì nằm bên phải, nhỏ hơn thì nằm bên trái.

n là một số tự nhiên lớn hơn 2 nên n nằm bên phải điểm 2 => B sai, C đúng
n là một số tự nhiên nhỏ hơn 5 nên n nằm bên trái điểm 2 =>A,D sai.
\(\overline {a001} \left( {a \ne 0} \right)\) bằng
\(\overline {a001} = a \times 1000 + 0 \times 100 + 0 \times 10 + 1\)
\(\overline {a001} = 1000 + 0 \times 100 + 0 \times 10 + 1\)
\(\overline {a001} = a \times 1000 + 1 \times 100\)
\(\overline {a001} = a + 0 + 0 + 1\)
Đáp án : A
- Xác định hàng của từng chữ số trong mỗi số.
- Chữ số hàng đơn vị ta giữ nguyên
- Chữ số hàng chục nhân với 10.
- Chữ số hàng trăm nhân với 100.
- Chữ số hàng nghìn nhân với 1000.
Số a là chữ số hàng nghìn nên ta nhân với 1000.
Hai số 0 lần lượt là hàng trăm (nhân với 100) và hàng chục (nhân với 10).
Số 1 là chữ số hàng đơn vị (nhân với 1).
\(\overline {a001} = a \times 1000 + 0 \times 100 + 0 \times 10 + 1\).
Viết số 24 bằng số La Mã
XXIIII
XXIX
XXIV
XIV
Đáp án : C
- Số từ 21 đến 30 ta viết chữ XX trước.
- Nếu hàng đơn vị là các số từ 1 đến 9 thì ghép chữ số La Mã tương ứng với nó như trong bảng vào.

Chữ số 4 là IV
Ta thêm XX vào bên trái số IV thì được số 24: XXIV
Số La Mã XXIV biểu diễn số nào trong hệ thập phân?
26
16
14
24
Đáp án : D
- Bên trái của số La Mã có hai chữ số XX liên tiếp thì đó là số từ 20 đến 29.
- Các chữ số sau XX là một trong các số từ 1 đến 9 như trong bảng sau:

X có giá trị bằng 10
IV có giá trị bằng 4 nên số XXIV biểu diễn số 10+10+4=24
Năm 2000 là thế kỉ bao nhiêu?
XX
XIX
XXI
XXX
Đáp án : A
Cứ 100 năm là 1 thế kỉ.
Thế kỉ I bắt đầu từ ngày 1 tháng 1 năm 1 và kết thúc vào ngày 31 tháng 12 năm 100.
Năm cuối cùng của thế kỉ XX là 2000.
Năm 2000 là thế kỉ XX.
Số liền trước số \(1000\) là
\(1002\)
\(990\)
\(1001\)
\(999\)
Đáp án : D
+ Hai số tự nhiên liên tiếp hơn kém nhau 1 đơn vị
+ Số tự nhiên liền trước số \(a\) là số $a - 1.$
Số tự nhiên liền trước số \(1000\) là số \(1000 - 1 = 999.\)
Số tự nhiên liền sau số \(2018\) là
\(2016\)
\(2017\)
\(2019\)
\(2020\)
Đáp án : C
+ Hai số tự nhiên liên tiếp hơn kém nhau 1 đơn vị nên số tự nhiên liền sau hơn số tự nhiên liền trước nó là \(1\) đơn vị.
Số tự nhiên liền sau số \(2018\) là số \(2018 + 1 = 2019.\)
Thay a và b bằng một số tự nhiên phù hợp trong trường hợp sau:
17, b, a là ba số lẻ liên tiếp tăng dần.
\(a = 21,b = 19\)
\(a = 19,b = 21\)
\(a = 13,b = 15\)
\(a = 15,b = 13\)
Đáp án : A
Các số lẻ liên tiếp cách nhau 2 đơn vị
b là số lẻ liền sau 17, a là số lẻ liền sau b.
17, b, a là ba số lẻ liên tiếp tăng dần nên các số đó lần lượt là 17, 19, 21.
Vậy \(a = 21,b = 19\)
Cho hai số tự nhiên \(99;100\). Hãy tìm số tự nhiên \(a\) để ba số có được tạo thành ba số tự nhiên liên tiếp.
\(98\)
\(97\)
\(101\)
Cả A, C đều đúng
Đáp án : D
Sử dụng các số tự nhiên liên tiếp hơn kém nhau \(1\) đơn vị để tìm các số thích hợp
Số liền trước số \(99\) là \(98\) nên ba số tự nhiên liên tiếp là \(98;99;100\)
Số liền sau số \(100\) là \(101\) nên ba số tự nhiên liên tiếp là \(99;100;101\)
Vậy cả hai số \(98;101\) đều thỏa mãn yêu cầu đề bài.
Tìm các số tự nhiên \(a,b,c\) sao cho \(228 \le a < b < c \le 230.\)
\(a = 228;b = 229;c = 230\)
\(a = 227;b = 228;c = 229\)
\(a = 229;b = 230;c = 231\)
Không tồn tại \(a;b;c\) thỏa mãn đề bài.
Đáp án : A
Tìm các số tự nhiên thỏa mãn đề bài rồi sắp xếp theo thứ tự tăng dần để tìm \(a;b;c.\)
Từ đề bài, ta thấy các số tự nhiên lớn hơn hoặc bằng \(228\) và nhỏ hơn hoặc bằng \(230\) là
\(228;229;230.\)
Mà \(a < b < c\) nên ta có \(a = 228;b = 229;c = 230.\)
Thêm chữ số \(7\) vào đằng trước số tự nhiên có ba chữ số thì ta được số tự nhiên mới
Hơn số tự nhiên cũ \(700\) đơn vị
Kém số tự nhiên cũ \(700\) đơn vị
Hơn số tự nhiên cũ \(7000\) đơn vị
Kém số tự nhiên cũ \(7000\) đơn vị
Đáp án : C
Sử dụng mối quan hệ giữa các chữ số trong số tự nhiên.
Trong hệ thập phân, cứ mười đơn vị của một hàng thì làm thành đơn vị của hàng liền trước đó.
Gọi số có ba số ban đầu là \(\overline {abc} \) , viết thêm chữ số \(7\) vào đằng trước ta được \(\overline {7abc} \) .
Ta có \(\overline {7abc} = 7000 + \overline {abc} \) nên số mới hơn số cũ \(7000\) đơn vị.
Với ba chữ số \(0;1;3\) có thể viết được bao nhiêu số có ba chữ số khác nhau?
\(4\)
\(3\)
\(5\)
\(6\)
Đáp án : A
- Ta viết các số tự nhiên có ba chữ số khác nhau lập thành từ ba số \(0;1;3\) sao cho chữ số hằng trăm khác \(0\).
- Đếm các số.
Có bốn số tự nhiên thỏa mãn đề bài là \(310;301;103;130.\)
Bài 2 trong chương trình Toán 6 Kết nối tri thức tập trung vào việc làm quen với cách ghi số tự nhiên và hiểu rõ thứ tự của chúng. Đây là nền tảng quan trọng để học tập các kiến thức toán học nâng cao hơn. Bài viết này sẽ cung cấp một cái nhìn tổng quan về các khái niệm chính, kèm theo các dạng bài tập trắc nghiệm thường gặp để giúp các em học sinh ôn tập và củng cố kiến thức.
Số tự nhiên là tập hợp các số được sử dụng để đếm. Tập hợp số tự nhiên được ký hiệu là ℕ và bao gồm các số 0, 1, 2, 3,...
Số tự nhiên được ghi bằng các chữ số từ 0 đến 9. Mỗi chữ số có một giá trị vị trí khác nhau, từ hàng đơn vị, hàng chục, hàng trăm,...
Ví dụ: Số 123 được đọc là một trăm hai mươi ba. Trong đó:
Trong tập hợp các số tự nhiên, ta có thể so sánh các số với nhau bằng các dấu >, <, =. Số nào đứng trước số khác trên trục số thì nhỏ hơn.
Ví dụ:
Bài tập yêu cầu xác định xem một số cho trước có phải là số tự nhiên hay không.
Ví dụ: Số -1 có phải là số tự nhiên không? (Đáp án: Không)
Bài tập yêu cầu sắp xếp một dãy số tự nhiên theo thứ tự từ nhỏ đến lớn hoặc từ lớn đến nhỏ.
Ví dụ: Sắp xếp các số sau theo thứ tự tăng dần: 5, 2, 8, 1 (Đáp án: 1, 2, 5, 8)
Bài tập yêu cầu so sánh hai số tự nhiên và điền dấu >, <, = vào chỗ trống.
Ví dụ: 15 ... 10 (Đáp án: >)
Bài tập yêu cầu tìm một số tự nhiên thỏa mãn một điều kiện nhất định.
Ví dụ: Tìm số tự nhiên x sao cho x + 5 = 12 (Đáp án: x = 7)
Dưới đây là một số bài tập trắc nghiệm minh họa để các em luyện tập:
(Đáp án: B)
(Đáp án: B)
(Đáp án: C)
Hi vọng với những kiến thức và bài tập trắc nghiệm trên, các em học sinh đã nắm vững kiến thức về cách ghi số tự nhiên và thứ tự trong tập hợp các số tự nhiên. Hãy luyện tập thường xuyên để đạt kết quả tốt nhất trong các bài kiểm tra và kỳ thi sắp tới.