Chào mừng các em học sinh lớp 6 đến với chuyên mục trắc nghiệm Toán 6 của giaitoan.edu.vn. Chuyên mục này tập trung vào các dạng bài tập về tập hợp các số nguyên, một trong những kiến thức nền tảng và quan trọng của chương trình Toán học lớp 6.
Với hình thức trắc nghiệm, các em sẽ được ôn luyện và củng cố kiến thức một cách nhanh chóng và hiệu quả.
Điểm cách \( - 1\) ba đơn vị theo chiều âm là
$3$
$ - 3$
$ - 4$
$4$
Điểm \(6\) cách điểm \(2\) bao nhiêu đơn vị?
$3$
$5$
$2$
$4$
Cho \(C = \left\{ { - 3; - 2;0;1;6;10} \right\}\). Viết tập hợp \(D\) gồm các phần tử thuộc \(C\) và là số nguyên âm.
\(D = \left\{ { - 3; - 2;0} \right\}.\)
\(D = \left\{ { - 3; - 2} \right\}.\)
\(D = \left\{ {0;1;6;10} \right\}.\)
\(D = \left\{ { - 3; - 2;6;10;1} \right\}.\)
Những điểm cách điểm \(0\) ba đơn vị là
$3$ và \( - 3\)
$2$ và \( - 2\)
$2$ và \( - 3\)
$3$ và \( - 2\)
Những điểm cách điểm 3 năm đơn vị là:
$7$ và \( - 1\)
$6$ và \( - 2\)
$2$ và \( - 2\)
$8$ và \( - 2\)
Có bao nhiêu số nguyên nằm giữa \( - 3\) và \(4\) là:
$3$
$5$
$6$
$7$
Trên trục số điểm A cách gốc $4$ đơn vị về phía bên trái, điểm B cách gốc $1$ đơn vị về phía bên phải. Hỏi điểm A cách điểm B bao nhiêu đơn vị?
$3$
$5$
$2$
$4$
Số cách số \( - 2\) sáu đơn vị theo chiều dương là?
$6$
$ - 8$
$4$
$5$
Một tàu ngầm đang ở vị trí dưới mực nước biển 120 m. Số nguyên âm biểu thị độ cao của tàu so với mực nước biển là:
Số nguyên âm biểu thị ông Hai nợ ngân hàng \(5\,000\,\,000\) đồng là:
Số nguyên âm biểu thị năm sự kiện: Thế vận hội đầu tiên diễn ra năm \(776\) trước công nguyên là:
Trong các số: \( - 2;\, - \dfrac{4}{3};\,4;\,0,5;\, - 100;\,1\dfrac{2}{7}\) có bao nhiêu số là số nguyên.
Cách viết nào sau đây là đúng:

Cho trục số:
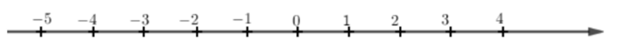
Điểm \( - 4\) cách điểm \(3\) bao nhiêu đơn vị?

Lời giải và đáp án
Điểm cách \( - 1\) ba đơn vị theo chiều âm là
$3$
$ - 3$
$ - 4$
$4$
Đáp án : C
- Sử dụng trục số để tìm đáp án
+ Trên trục số: Điểm \(0\) được gọi là điểm gốc của trục số. Chiều từ trái sang phải gọi là chiều dương (thường được đánh dấu bằng mũi tên), chiều từ phải sang trái gọi là chiều âm của trục số.
Điểm cách $ - 1$ ba đơn vị theo chiều âm là điểm nằm phía bên trái điểm $ - 1$ và cách điểm $ - 1$ ba đơn vị.
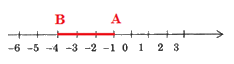
Điểm nằm bên trái điểm $ - 1$ và cách điểm $ - 1$ ba đơn vị là điểm $ - 4$ Nên điểm cách $ - 1$ ba đơn vị theo chiều âm là $ - 4.$
Điểm \(6\) cách điểm \(2\) bao nhiêu đơn vị?
$3$
$5$
$2$
$4$
Đáp án : D
- Sử dụng kiến thức về trục số để xác định khoảng cách từ điểm \(6\) đến điểm \(2\).
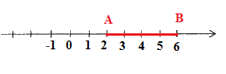
Điểm \(6\) cách điểm \(2\) là bốn đơn vị
Cho \(C = \left\{ { - 3; - 2;0;1;6;10} \right\}\). Viết tập hợp \(D\) gồm các phần tử thuộc \(C\) và là số nguyên âm.
\(D = \left\{ { - 3; - 2;0} \right\}.\)
\(D = \left\{ { - 3; - 2} \right\}.\)
\(D = \left\{ {0;1;6;10} \right\}.\)
\(D = \left\{ { - 3; - 2;6;10;1} \right\}.\)
Đáp án : B
- Chọn ra các số nguyên âm trong các phần tử thuộc tập hợp \(C.\)
- Viết tập hợp \(D\) gồm các phần tử là các số vừa tìm được.
Ta có \(C = \left\{ { - 3; - 2;0;1;6;10} \right\}\) có các số nguyên âm là \( - 3; - 2\). Nên tập hợp \(D = \left\{ { - 3; - 2} \right\}.\)
Những điểm cách điểm \(0\) ba đơn vị là
$3$ và \( - 3\)
$2$ và \( - 2\)
$2$ và \( - 3\)
$3$ và \( - 2\)
Đáp án : A
Những điểm cách điểm $0$ ba đơn vị là điểm nằm bên phải điểm $0$ và cách điểm $0$ ba đơn vị, điểm nằm bên trái điểm $0$ và cách điểm $0$ ba đơn vị.
Điểm nằm bên phải điểm $0$ và cách điểm $0$ ba đơn vị là: $3$ Điểm nằm bên trái điểm $0$ và cách điểm $0$ ba đơn vị là: $ - 3$.
Những điểm cách điểm 3 năm đơn vị là:
$7$ và \( - 1\)
$6$ và \( - 2\)
$2$ và \( - 2\)
$8$ và \( - 2\)
Đáp án : D
Những điểm cách điểm $3$ năm đơn vị là điểm nằm bên phải điểm $3$ và cách điểm $3$ năm đơn vị, điểm nằm bên trái điểm $3$ và cách điểm $3$ năm đơn vị.
Điểm nằm bên phải điểm $3$ và cách điểm $3$ năm đơn vị là: $8$ Điểm nằm bên trái điểm $3$ và cách điểm $3$ năm đơn vị là: $ - 2$
Có bao nhiêu số nguyên nằm giữa \( - 3\) và \(4\) là:
$3$
$5$
$6$
$7$
Đáp án : C
Các số nằm giữa $ - 3$ và $4$ là các số nằm bên phải $ - 3$ và bên trái của $4$ trên trục số.

Các số nằm giữa $ - 3$ và $4$ là: \( - 2; - 1;0;1;2;3.\)
Vậy có \(6\) số thỏa mãn điều kiện đề bài.
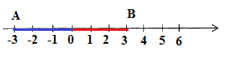
Trên trục số điểm A cách gốc $4$ đơn vị về phía bên trái, điểm B cách gốc $1$ đơn vị về phía bên phải. Hỏi điểm A cách điểm B bao nhiêu đơn vị?
$3$
$5$
$2$
$4$
Đáp án : B
Dựa vào trục số để xác định.Lưu ý: Gốc trên trục tọa độ là điểm $0.$
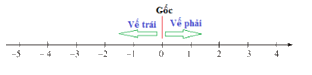
Quan sát trục số ta thấy:Điểm cách gốc $4$ đơn vị vế phía bên trái là điểm $ - 4,$ nên điểm A biểu diễn số: $ - 4$Điểm cách gốc $1$ đơn vị về phía bên phải là: $1$, nên điểm B biểu diễn số $1.$
Điểm $ - 4$ cách điểm $1$ là năm đơn vị.
Vậy điểm A cách điểm B là $5$ đơn vị.
Số cách số \( - 2\) sáu đơn vị theo chiều dương là?
$6$
$ - 8$
$4$
$5$
Đáp án : C
Điểm nằm cách điểm A theo chiều dương tức là điểm đó nằm bên tay phải điểm AĐiểm nằm cách điểm A theo chiều âm tức là điểm đó nằm bên trái điểm A

Ta đếm về bên phải số $ - 2$ sáu đơn vị được số $4$ ( hay $ + 4$ )Vậy số cách số $ - 2$ sáu đơn vị theo chiều dương là: $4$ ( hay $ + 4$)
Một tàu ngầm đang ở vị trí dưới mực nước biển 120 m. Số nguyên âm biểu thị độ cao của tàu so với mực nước biển là:
Đáp án : B
Số nguyên âm biểu thị vị trí dưới mực nước biển \(a\,\,\left( m \right)\) là: \( - a\,\,\left( m \right)\).
Số nguyên âm biểu thị độ cao của tàu so với mực nước biển là: \( - 120\,\,m\).
Số nguyên âm biểu thị ông Hai nợ ngân hàng \(5\,000\,\,000\) đồng là:
Đáp án : C
Số nguyên âm biểu thị số tiền nợ (lỗ) \(a\,\,\)đồng là: \( - a\,\,\) đồng.
Do ông Hai nợ ngân hàng \(5\,000\,\,000\) đồng nên ta có thể nói ông Hai có \( - \,5\,\,000\,\,000\) đồng.
Số nguyên âm biểu thị năm sự kiện: Thế vận hội đầu tiên diễn ra năm \(776\) trước công nguyên là:
Đáp án : B
Số nguyên âm biểu thị năm \(a\) trước công nguyên là: \( - a\).
Thế vận hội đầu tiên diễn ra năm \(776\) trước công nguyên tức là nó diễn ra vào năm \( - 776\)
Trong các số: \( - 2;\, - \dfrac{4}{3};\,4;\,0,5;\, - 100;\,1\dfrac{2}{7}\) có bao nhiêu số là số nguyên.
Đáp án : C
Tập hợp số gồm các số nguyên âm, số \(0\) và các số nguyên dương được gọi là tập hợp số nguyên.
Các số \(- \dfrac{4}{3};\,0,5;\,1\dfrac{2}{7}\) không phải là số nguyên.
Các số là số nguyên là: \( - 2;\,\,4;\, - 100\).
Vậy có \(3\) số là số nguyên.
Cách viết nào sau đây là đúng:
Đáp án : C
\(\begin{array}{l}\mathbb{N} = \left\{ {0;\,\,1;\,\,2;\,\,3;\,...} \right\}\\\mathbb{Z} = \left\{ {...;\, - 2;\, - 1;\,0;\,\,1;\,\,2;...} \right\}\end{array}\)
\( - 2\) không là số tự nhiên => Asai.
\(1,5\) và \(1\dfrac{1}{2}\) không là số nguyên => B, Dsai.
\( - 31\) là số nguyên => Cđúng.

Đáp án : B
Cho trục số:
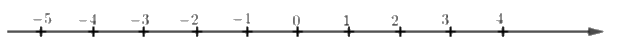
Điểm \( - 4\) cách điểm \(3\) bao nhiêu đơn vị?
Đáp án : C
Đếm xem điểm \( - 4\) cách điểm \(3\) bao nhiêu khoảng, mỗi khoảng là 1 đơn vị.
Ta thấy điểm \( - 4\) cách điểm \(3\) bảy đơn vị.

Đáp án : B
Hai vạch liên tiếp của nhiệt kế cách nhau 1 đơn vị.
Coi nhiệt kế như trục số thẳng đứng, chiều dương từ dưới lên trên.
Điểm cách \( - 1\) ba đơn vị theo chiều âm là
$3$
$ - 3$
$ - 4$
$4$
Điểm \(6\) cách điểm \(2\) bao nhiêu đơn vị?
$3$
$5$
$2$
$4$
Cho \(C = \left\{ { - 3; - 2;0;1;6;10} \right\}\). Viết tập hợp \(D\) gồm các phần tử thuộc \(C\) và là số nguyên âm.
\(D = \left\{ { - 3; - 2;0} \right\}.\)
\(D = \left\{ { - 3; - 2} \right\}.\)
\(D = \left\{ {0;1;6;10} \right\}.\)
\(D = \left\{ { - 3; - 2;6;10;1} \right\}.\)
Những điểm cách điểm \(0\) ba đơn vị là
$3$ và \( - 3\)
$2$ và \( - 2\)
$2$ và \( - 3\)
$3$ và \( - 2\)
Những điểm cách điểm 3 năm đơn vị là:
$7$ và \( - 1\)
$6$ và \( - 2\)
$2$ và \( - 2\)
$8$ và \( - 2\)
Có bao nhiêu số nguyên nằm giữa \( - 3\) và \(4\) là:
$3$
$5$
$6$
$7$
Trên trục số điểm A cách gốc $4$ đơn vị về phía bên trái, điểm B cách gốc $1$ đơn vị về phía bên phải. Hỏi điểm A cách điểm B bao nhiêu đơn vị?
$3$
$5$
$2$
$4$
Số cách số \( - 2\) sáu đơn vị theo chiều dương là?
$6$
$ - 8$
$4$
$5$
Một tàu ngầm đang ở vị trí dưới mực nước biển 120 m. Số nguyên âm biểu thị độ cao của tàu so với mực nước biển là:
Số nguyên âm biểu thị ông Hai nợ ngân hàng \(5\,000\,\,000\) đồng là:
Số nguyên âm biểu thị năm sự kiện: Thế vận hội đầu tiên diễn ra năm \(776\) trước công nguyên là:
Trong các số: \( - 2;\, - \dfrac{4}{3};\,4;\,0,5;\, - 100;\,1\dfrac{2}{7}\) có bao nhiêu số là số nguyên.
Cách viết nào sau đây là đúng:

Cho trục số:
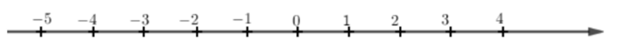
Điểm \( - 4\) cách điểm \(3\) bao nhiêu đơn vị?

Điểm cách \( - 1\) ba đơn vị theo chiều âm là
$3$
$ - 3$
$ - 4$
$4$
Đáp án : C
- Sử dụng trục số để tìm đáp án
+ Trên trục số: Điểm \(0\) được gọi là điểm gốc của trục số. Chiều từ trái sang phải gọi là chiều dương (thường được đánh dấu bằng mũi tên), chiều từ phải sang trái gọi là chiều âm của trục số.
Điểm cách $ - 1$ ba đơn vị theo chiều âm là điểm nằm phía bên trái điểm $ - 1$ và cách điểm $ - 1$ ba đơn vị.

Điểm nằm bên trái điểm $ - 1$ và cách điểm $ - 1$ ba đơn vị là điểm $ - 4$ Nên điểm cách $ - 1$ ba đơn vị theo chiều âm là $ - 4.$
Điểm \(6\) cách điểm \(2\) bao nhiêu đơn vị?
$3$
$5$
$2$
$4$
Đáp án : D
- Sử dụng kiến thức về trục số để xác định khoảng cách từ điểm \(6\) đến điểm \(2\).

Điểm \(6\) cách điểm \(2\) là bốn đơn vị
Cho \(C = \left\{ { - 3; - 2;0;1;6;10} \right\}\). Viết tập hợp \(D\) gồm các phần tử thuộc \(C\) và là số nguyên âm.
\(D = \left\{ { - 3; - 2;0} \right\}.\)
\(D = \left\{ { - 3; - 2} \right\}.\)
\(D = \left\{ {0;1;6;10} \right\}.\)
\(D = \left\{ { - 3; - 2;6;10;1} \right\}.\)
Đáp án : B
- Chọn ra các số nguyên âm trong các phần tử thuộc tập hợp \(C.\)
- Viết tập hợp \(D\) gồm các phần tử là các số vừa tìm được.
Ta có \(C = \left\{ { - 3; - 2;0;1;6;10} \right\}\) có các số nguyên âm là \( - 3; - 2\). Nên tập hợp \(D = \left\{ { - 3; - 2} \right\}.\)
Những điểm cách điểm \(0\) ba đơn vị là
$3$ và \( - 3\)
$2$ và \( - 2\)
$2$ và \( - 3\)
$3$ và \( - 2\)
Đáp án : A
Những điểm cách điểm $0$ ba đơn vị là điểm nằm bên phải điểm $0$ và cách điểm $0$ ba đơn vị, điểm nằm bên trái điểm $0$ và cách điểm $0$ ba đơn vị.

Điểm nằm bên phải điểm $0$ và cách điểm $0$ ba đơn vị là: $3$ Điểm nằm bên trái điểm $0$ và cách điểm $0$ ba đơn vị là: $ - 3$.
Những điểm cách điểm 3 năm đơn vị là:
$7$ và \( - 1\)
$6$ và \( - 2\)
$2$ và \( - 2\)
$8$ và \( - 2\)
Đáp án : D
Những điểm cách điểm $3$ năm đơn vị là điểm nằm bên phải điểm $3$ và cách điểm $3$ năm đơn vị, điểm nằm bên trái điểm $3$ và cách điểm $3$ năm đơn vị.
Điểm nằm bên phải điểm $3$ và cách điểm $3$ năm đơn vị là: $8$ Điểm nằm bên trái điểm $3$ và cách điểm $3$ năm đơn vị là: $ - 2$
Có bao nhiêu số nguyên nằm giữa \( - 3\) và \(4\) là:
$3$
$5$
$6$
$7$
Đáp án : C
Các số nằm giữa $ - 3$ và $4$ là các số nằm bên phải $ - 3$ và bên trái của $4$ trên trục số.

Các số nằm giữa $ - 3$ và $4$ là: \( - 2; - 1;0;1;2;3.\)
Vậy có \(6\) số thỏa mãn điều kiện đề bài.
Trên trục số điểm A cách gốc $4$ đơn vị về phía bên trái, điểm B cách gốc $1$ đơn vị về phía bên phải. Hỏi điểm A cách điểm B bao nhiêu đơn vị?
$3$
$5$
$2$
$4$
Đáp án : B
Dựa vào trục số để xác định.Lưu ý: Gốc trên trục tọa độ là điểm $0.$

Quan sát trục số ta thấy:Điểm cách gốc $4$ đơn vị vế phía bên trái là điểm $ - 4,$ nên điểm A biểu diễn số: $ - 4$Điểm cách gốc $1$ đơn vị về phía bên phải là: $1$, nên điểm B biểu diễn số $1.$
Điểm $ - 4$ cách điểm $1$ là năm đơn vị.
Vậy điểm A cách điểm B là $5$ đơn vị.
Số cách số \( - 2\) sáu đơn vị theo chiều dương là?
$6$
$ - 8$
$4$
$5$
Đáp án : C
Điểm nằm cách điểm A theo chiều dương tức là điểm đó nằm bên tay phải điểm AĐiểm nằm cách điểm A theo chiều âm tức là điểm đó nằm bên trái điểm A

Ta đếm về bên phải số $ - 2$ sáu đơn vị được số $4$ ( hay $ + 4$ )Vậy số cách số $ - 2$ sáu đơn vị theo chiều dương là: $4$ ( hay $ + 4$)
Một tàu ngầm đang ở vị trí dưới mực nước biển 120 m. Số nguyên âm biểu thị độ cao của tàu so với mực nước biển là:
Đáp án : B
Số nguyên âm biểu thị vị trí dưới mực nước biển \(a\,\,\left( m \right)\) là: \( - a\,\,\left( m \right)\).
Số nguyên âm biểu thị độ cao của tàu so với mực nước biển là: \( - 120\,\,m\).
Số nguyên âm biểu thị ông Hai nợ ngân hàng \(5\,000\,\,000\) đồng là:
Đáp án : C
Số nguyên âm biểu thị số tiền nợ (lỗ) \(a\,\,\)đồng là: \( - a\,\,\) đồng.
Do ông Hai nợ ngân hàng \(5\,000\,\,000\) đồng nên ta có thể nói ông Hai có \( - \,5\,\,000\,\,000\) đồng.
Số nguyên âm biểu thị năm sự kiện: Thế vận hội đầu tiên diễn ra năm \(776\) trước công nguyên là:
Đáp án : B
Số nguyên âm biểu thị năm \(a\) trước công nguyên là: \( - a\).
Thế vận hội đầu tiên diễn ra năm \(776\) trước công nguyên tức là nó diễn ra vào năm \( - 776\)
Trong các số: \( - 2;\, - \dfrac{4}{3};\,4;\,0,5;\, - 100;\,1\dfrac{2}{7}\) có bao nhiêu số là số nguyên.
Đáp án : C
Tập hợp số gồm các số nguyên âm, số \(0\) và các số nguyên dương được gọi là tập hợp số nguyên.
Các số \(- \dfrac{4}{3};\,0,5;\,1\dfrac{2}{7}\) không phải là số nguyên.
Các số là số nguyên là: \( - 2;\,\,4;\, - 100\).
Vậy có \(3\) số là số nguyên.
Cách viết nào sau đây là đúng:
Đáp án : C
\(\begin{array}{l}\mathbb{N} = \left\{ {0;\,\,1;\,\,2;\,\,3;\,...} \right\}\\\mathbb{Z} = \left\{ {...;\, - 2;\, - 1;\,0;\,\,1;\,\,2;...} \right\}\end{array}\)
\( - 2\) không là số tự nhiên => Asai.
\(1,5\) và \(1\dfrac{1}{2}\) không là số nguyên => B, Dsai.
\( - 31\) là số nguyên => Cđúng.

Đáp án : B
Cho trục số:
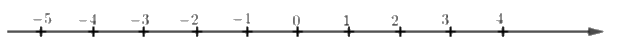
Điểm \( - 4\) cách điểm \(3\) bao nhiêu đơn vị?
Đáp án : C
Đếm xem điểm \( - 4\) cách điểm \(3\) bao nhiêu khoảng, mỗi khoảng là 1 đơn vị.
Ta thấy điểm \( - 4\) cách điểm \(3\) bảy đơn vị.

Đáp án : B
Hai vạch liên tiếp của nhiệt kế cách nhau 1 đơn vị.
Coi nhiệt kế như trục số thẳng đứng, chiều dương từ dưới lên trên.
Chương trình Toán 6 Kết nối tri thức giới thiệu về tập hợp các số nguyên, bao gồm số nguyên âm, số nguyên dương và số 0. Việc nắm vững kiến thức về tập hợp số nguyên là nền tảng quan trọng để học tốt các kiến thức toán học ở các lớp trên. Các dạng bài tập thường gặp liên quan đến tập hợp số nguyên bao gồm:
Bài tập dạng này yêu cầu học sinh xác định xem một số cho trước có phải là số nguyên hay không. Để giải bài tập này, học sinh cần nắm vững định nghĩa về số nguyên: số nguyên là tập hợp bao gồm các số nguyên âm, số nguyên dương và số 0.
Ví dụ: Số -3 có phải là số nguyên không? Đáp án: Có
Bài tập dạng này yêu cầu học sinh so sánh hai hoặc nhiều số nguyên. Để so sánh các số nguyên, học sinh cần nhớ quy tắc sau:
Ví dụ: So sánh -5 và -2. Đáp án: -5 < -2
Bài tập dạng này yêu cầu học sinh sắp xếp các số nguyên theo thứ tự tăng dần hoặc giảm dần. Để giải bài tập này, học sinh cần áp dụng quy tắc so sánh số nguyên đã học.
Ví dụ: Sắp xếp các số nguyên sau theo thứ tự tăng dần: -3, 0, 2, -1. Đáp án: -3, -1, 0, 2
Bài tập dạng này yêu cầu học sinh biểu diễn các số nguyên trên trục số. Để giải bài tập này, học sinh cần hiểu rõ cách xây dựng trục số và vị trí của các số nguyên trên trục số.
Ví dụ: Biểu diễn số -4 trên trục số.
Bài tập dạng này yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia với số nguyên. Để giải bài tập này, học sinh cần nắm vững các quy tắc thực hiện các phép toán với số nguyên.
Ví dụ: Tính: -5 + 3. Đáp án: -2
Để nắm vững kiến thức về tập hợp các số nguyên và làm tốt các bài tập trắc nghiệm, các em cần luyện tập thường xuyên. Hãy truy cập giaitoan.edu.vn để luyện tập với nhiều bài tập trắc nghiệm khác nhau. Chúc các em học tốt!
| Quy tắc | Mô tả |
|---|---|
| So sánh số nguyên âm | Số nào có giá trị tuyệt đối lớn hơn thì nhỏ hơn. |
| Cộng hai số nguyên âm | Cộng giá trị tuyệt đối của chúng và giữ dấu âm. |
| Trừ hai số nguyên âm | Trừ giá trị tuyệt đối của chúng và giữ dấu âm. |