Chào mừng các em học sinh lớp 6 đến với chuyên mục Trắc nghiệm Bài tập cuối chương II môn Toán 6 chương trình Kết nối tri thức. Tại giaitoan.edu.vn, chúng tôi cung cấp bộ đề trắc nghiệm đa dạng, bám sát nội dung sách giáo khoa, giúp các em ôn luyện kiến thức một cách hiệu quả.
Các bài tập trắc nghiệm này được thiết kế để kiểm tra và củng cố những kiến thức trọng tâm của chương II, bao gồm các chủ đề như số nguyên, phép toán trên số nguyên, và các bài toán thực tế liên quan.
$BCNN(9;24)$ là bao nhiêu?
$54$
$18$
$72$
$36$
Cho $36 = {2^2}{.3^2};60 = {2^2}.3.5;72 = {2^3}{.3^2}$. Ta có $ƯCLN(36;60;72)$là:
${2^3}.3.5$
${2^2}{.3^2}$
${2^2}.3$
$3.5$
Chọn câu đúng. $BCNN\left( {18;{\rm{ }}32;{\rm{ }}50} \right)$ là một số:
Có tổng các chữ số là $10$
Lẻ
Chia hết cho $10$
Có chữ số hàng đơn vị là $5$
Tìm số tự nhiên $a, b$ thỏa mãn $\overline {2a4b} $ chia hết cho các số $2; 3; 5$ và $9.$
$a = 3;b = 0$
$b = 3;a = 0$
$a = 1;b = 2$
$a = 9;b = 0$
Tìm số tự nhiên a lớn nhất biết: $525\,\; \vdots \;\,a;{\rm{ }}875\;\, \vdots \;\,a;{\rm{ }}280\,\; \vdots \;\,a\;$
$125$
$25$
$175$
$35$
Có bao nhiêu số tự nhiên \(x\) biết \(x \vdots 5;x \vdots 6\) và \(0 < x < 100\).
$1$
$2$
$5$
$3$
Cho $A = 18 + 36 + 72 + 2x$. Tìm giá trị của $x$ biết rằng $A$ chia hết cho $9$ và $45 < x < 55$
$x = 45$
$x = 54$
A, B đều sai
A, B đều đúng
Một trường học có khoảng từ 100 đến 150 học sinh khối 6. Khi xếp thành 10 hàng, 12 hàng, 15 hàng đều vừa đủ. Vậy hỏi số học sinh khối 6 của trường đó là bao nhiêu?
$110$
$120$
$140$
$125$
Một buổi liên hoan ban tổ chức đã mua tất cả 840 cái bánh, 2352 cái kẹo và 560 quả quýt chia đều ra các đĩa, mỗi đĩa gồm cả bánh, kẹo và quýt. Tính số đĩa nhiều nhất mà ban tổ chức phải chuẩn bị?
$28$
$48$
$63$
$56$
Cho 2 số: $14n + 3$ và $21n + 4$ với $n$ là số tự nhiên, chọn đáp án đúng.
Hai số trên có hai ước chung
Hai số trên có ba ước chung
Hai số trên là hai số nguyên tố cùng nhau
Hai số trên chỉ có một ước chung là 3.
Lời giải và đáp án
$BCNN(9;24)$ là bao nhiêu?
$54$
$18$
$72$
$36$
Đáp án : C
Bước 1 : Phân tích mỗi số ra thừa số nguyên tố.
Bước 2 : Chọn ra các thừa số nguyên tố chung và riêng.
Bước 3 : Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.
Ta có:
$\begin{array}{l}9 = {3^2};24 = {2^3}.3\\ \Rightarrow BCNN\left( {9;24} \right) = {2^3}{.3^2} = 8.9 = 72\end{array}$
Cho $36 = {2^2}{.3^2};60 = {2^2}.3.5;72 = {2^3}{.3^2}$. Ta có $ƯCLN(36;60;72)$là:
${2^3}.3.5$
${2^2}{.3^2}$
${2^2}.3$
$3.5$
Đáp án : C
Áp dụng phương pháp tìm ƯCLN: phân tích các số ra thừa số nguyên tố, chọn các thừa số chung. Mỗi thừa số lấy số mũ nhỏ nhất, tích của các số đó là ƯCLN
$36 = {2^2}{.3^2};60 = {2^2}.3.5;72 = {2^3}{.3^2}$
Ta số thừa số chung là $2;3$
Số mũ nhỏ nhất của $2$ là $2$; số mũ nhỏ nhất của $3$ là $1$
Vậy $ƯCLN\left( {36;60;72} \right) = {2^2}.3$.
Chọn câu đúng. $BCNN\left( {18;{\rm{ }}32;{\rm{ }}50} \right)$ là một số:
Có tổng các chữ số là $10$
Lẻ
Chia hết cho $10$
Có chữ số hàng đơn vị là $5$
Đáp án : C
Bước 1: Phân tích 18; 32 và 50 ra thừa số nguyên tố Bước 2: Chọn ra thừa số nguyên tố chung và riêng của 18; 32 và 50 Bước 3: Lập tích các thừa số nguyên tố đã chọn mỗi thừa số lấy với số mũ lớn nhất của nó Tích đó chính là $BCNN\left( {18;32;50} \right)$
Ta có \(18 = {2.3^2};32 = {2^5};50 = {2.5^2}\)
Nên \(BCNN\left( {18;32;50} \right) = {2^5}{.3^2}{.5^2} = 7200.\)
Vì $7200$ chia hết cho $10$ nên $C$ đúng.
Tìm số tự nhiên $a, b$ thỏa mãn $\overline {2a4b} $ chia hết cho các số $2; 3; 5$ và $9.$
$a = 3;b = 0$
$b = 3;a = 0$
$a = 1;b = 2$
$a = 9;b = 0$
Đáp án : A
Bước 1: Xác định b bằng tính chất: “ Một số chia hết cho $2$ và $5$ thì có chữ số tận cùng bằng $0$” Bước 2: Thay b vào rồi tính tổng các chữ số của $\overline {2a4b} $Để $\overline {2a4b} $ chia hết cho $3$ và $9$ thì tổng các chữ số phải chia hết cho $9$ Thử lần lượt các giá trị $a = 0,1,2,...,9$ vào xem giá trị nào thích hợp
Ta có: Để $\overline {2a4b} $ chia hết cho $2$ và $5$ thì $b = 0\;$ Thay $b = 0\;$ vào $\overline {2a4b} $ ta được $\overline {2a40} $ Tổng các chữ số là: \(2 + a + 4 + 0 = a + 6\) Thử lần lượt các giá trị $a = 0,1,2,...,9$Ta thấy với \(a = 3\) thì tổng các chữ số của $\overline {2a40} = 2340$ là: \(6 + 3 = 9\, \vdots \,9\)
Nên \(2340\) chia hết cho $3$ và $9$.
Vậy với \(a = 3;b = 0\) thì \(\overline {2a4b} \) chia hết cho \(2;3;5\) và \(9.\)
Tìm số tự nhiên a lớn nhất biết: $525\,\; \vdots \;\,a;{\rm{ }}875\;\, \vdots \;\,a;{\rm{ }}280\,\; \vdots \;\,a\;$
$125$
$25$
$175$
$35$
Đáp án : D
Ta đưa về bài toán tìm $ƯCLN$ của $525; 875; 280.$Bước 1: Phân tích $525; 875; 280$ ra thừa số nguyên tố.Bước 2: Chọn ra các thừa số nguyên tố chung.Bước 3: Lập tích các thừa số nguyên tố chung đó, mỗi thừa số lấy với số mũ nhỏ nhất của nó.Đó chính là số cần tìm.
Vì $525\,\; \vdots \;\,a;{\rm{ }}875\;\, \vdots \;\,a;{\rm{ }}280\,\; \vdots \;\,a\;$ và $a$ là số lớn nhất$ \Rightarrow a = ƯCLN\left( {525;{\rm{ }}875;{\rm{ }}280} \right)$ Ta có:
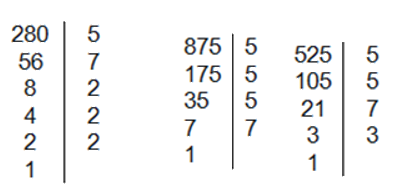
Nên \(525 = {3.5^2}.7;875 = {5^3}.7;280 = {2^3}.5.7\) $ \Rightarrow \;a = $ ƯCLN$\left( {525;875;280} \right) = 5.7 = 35\;$
Có bao nhiêu số tự nhiên \(x\) biết \(x \vdots 5;x \vdots 6\) và \(0 < x < 100\).
$1$
$2$
$5$
$3$
Đáp án : D
+ Tìm bội chung của \(5\) và \(6\)
+ Kết hợp với điều kiện \(0 < x < 100\) để tìm các số thỏa mãn.
Vì \(x \vdots 5;x \vdots 6\) nên \(x \in BC\left( {5;6} \right) = \left\{ {0;30;60;90;120;...} \right\}\)
Mà \(0 < x < 100\) nên \(x \in \left\{ {30;60;90} \right\}\).
Vậy \(x \in \left\{ {30;60;90} \right\}\).
Cho $A = 18 + 36 + 72 + 2x$. Tìm giá trị của $x$ biết rằng $A$ chia hết cho $9$ và $45 < x < 55$
$x = 45$
$x = 54$
A, B đều sai
A, B đều đúng
Đáp án : B
Áp dụng kiến thức về dấu hiệu chia hết:
Dấu hiệu chia hết cho $9$ là tổng tất cả các chữ số chia hết cho $9$
Dấu hiệu chia hết của $1$ tổng: nếu $a \vdots c;b \vdots c \Rightarrow (a + b) \vdots c$
Ta có $A = 18 + 36 + 72 + 2x$ mà $A \vdots 9;18 \vdots 9;36 \vdots 9;72 \vdots 9 \Rightarrow 2x \vdots 9 \Rightarrow x \vdots 9$
Mà $45 < x < 55 \Rightarrow x = 54$
Vậy $x = 54$.
Một trường học có khoảng từ 100 đến 150 học sinh khối 6. Khi xếp thành 10 hàng, 12 hàng, 15 hàng đều vừa đủ. Vậy hỏi số học sinh khối 6 của trường đó là bao nhiêu?
$110$
$120$
$140$
$125$
Đáp án : B
Áp dụng kiến thức về bội chung, nếu $a \vdots b;a \vdots c;a \vdots d$ thì $a$ là bội chung của $b,c,d$.
Từ đề bài suy ra số học sinh khối 6 là bội của 10;12;15.
Kết hợp điều kiện số học sinh trong khoảng từ 100 đến 150 để tìm số thích hợp
Gọi số học sinh khối 6 là \(x\left( {x \in {N^*}} \right)\) (học sinh)
Theo bài ra ta có:
\(x \vdots 10,x \vdots 12;x \vdots 15 \Rightarrow x \in BC\left( {10;12;15} \right)\) và \(100 \le x \le 150\).
Ta có
$\begin{array}{l}10 = 2.5;12 = {2^2}.3;15 = 3.5\\ \Rightarrow BCNN(10;12;15) = {2^2}.3.5 = 60\\ \Rightarrow BC\left( {10;12;15} \right) = \left\{ {0;60;120;180;...} \right\}\\ \Rightarrow x \in \left\{ {0;60;120;180;...} \right\} \end{array}$
Mà \(100 \le x \le 150\) nên \(x = 120\).
Vậy số học sinh khổi 6 là $120$ bạn.
Một buổi liên hoan ban tổ chức đã mua tất cả 840 cái bánh, 2352 cái kẹo và 560 quả quýt chia đều ra các đĩa, mỗi đĩa gồm cả bánh, kẹo và quýt. Tính số đĩa nhiều nhất mà ban tổ chức phải chuẩn bị?
$28$
$48$
$63$
$56$
Đáp án : D
Bước 1: Nếu gọi số đĩa là x cái, lập luận để có $x = $ƯCLN$\left( {840;2352;560} \right)$ Bước 2: Phân tích các số $840;{\rm{ }}2352;{\rm{ }}560$ ra thừa số nguyên tố Bước 3: Lập tích các thừa số nguyên tố chung, mỗi thừa số lấy với số mũ nhỏ nhất Đó chính là số đĩa cần tìm
Gọi số đĩa cần chẩn bị là x cái \(\left( {x \in {N^*}} \right)\) Vì số bánh, kẹo và quýt được chia đều vào các đĩa nên: $840\;\, \vdots x{\rm{ }};{\rm{ }}2352\,\; \vdots \;x{\rm{ }};{\rm{ }}560\;\, \vdots \;x$ Và $x$ là lớn nhất nên $x = $ƯCLN$\left( {840;2352;560} \right)$Ta có: \(840 = {2^3}.3.5.7;560 = {2^4}.5.7;2352 = {2^4}{.3.7^2}\)
Suy ra ƯCLN$\left( {840;{\rm{ }}2352;{\rm{ }}560} \right){\rm{ }} = \;{2^3}.7\; = 56$ Vậy số đĩa nhiều nhất cần chuẩn bị là $56$ .
Cho 2 số: $14n + 3$ và $21n + 4$ với $n$ là số tự nhiên, chọn đáp án đúng.
Hai số trên có hai ước chung
Hai số trên có ba ước chung
Hai số trên là hai số nguyên tố cùng nhau
Hai số trên chỉ có một ước chung là 3.
Đáp án : C
Dựa vào kiến thức 2 số nguyên tố cùng nhau là 2 số nguyên tố có ước chung lớn nhất là 1.
Áp dụng tính chất chia hết của 1 hiệu: Nếu $a \vdots c;b \vdots c \Rightarrow \left( {a - b} \right) \vdots c$
Gọi \(d = UCLN\left( {14n + 3;21n + 4} \right)\) ta có:
\(14n + 3\, \vdots \,d\) và \(21n + 4 \, \vdots \, d\)
\(3\left( {14n + 3} \right) \vdots \, d\) và \(2\left( {21n + 4} \right) \vdots d\)
\(42n + 9 \,\vdots \, d\) và \(42n + 8 \, \vdots \, d\)
\(\left( {42n + 9} \right) - \left( {42n + 8} \right) \vdots d\)
Suy ra \(1 \vdots d\)
\(d = 1\)
Vậy \(ƯCLN\left( {14n + 3;21n + 4} \right) = 1\) hay hai số đó là hai số nguyên tố cùng nhau.
$BCNN(9;24)$ là bao nhiêu?
$54$
$18$
$72$
$36$
Cho $36 = {2^2}{.3^2};60 = {2^2}.3.5;72 = {2^3}{.3^2}$. Ta có $ƯCLN(36;60;72)$là:
${2^3}.3.5$
${2^2}{.3^2}$
${2^2}.3$
$3.5$
Chọn câu đúng. $BCNN\left( {18;{\rm{ }}32;{\rm{ }}50} \right)$ là một số:
Có tổng các chữ số là $10$
Lẻ
Chia hết cho $10$
Có chữ số hàng đơn vị là $5$
Tìm số tự nhiên $a, b$ thỏa mãn $\overline {2a4b} $ chia hết cho các số $2; 3; 5$ và $9.$
$a = 3;b = 0$
$b = 3;a = 0$
$a = 1;b = 2$
$a = 9;b = 0$
Tìm số tự nhiên a lớn nhất biết: $525\,\; \vdots \;\,a;{\rm{ }}875\;\, \vdots \;\,a;{\rm{ }}280\,\; \vdots \;\,a\;$
$125$
$25$
$175$
$35$
Có bao nhiêu số tự nhiên \(x\) biết \(x \vdots 5;x \vdots 6\) và \(0 < x < 100\).
$1$
$2$
$5$
$3$
Cho $A = 18 + 36 + 72 + 2x$. Tìm giá trị của $x$ biết rằng $A$ chia hết cho $9$ và $45 < x < 55$
$x = 45$
$x = 54$
A, B đều sai
A, B đều đúng
Một trường học có khoảng từ 100 đến 150 học sinh khối 6. Khi xếp thành 10 hàng, 12 hàng, 15 hàng đều vừa đủ. Vậy hỏi số học sinh khối 6 của trường đó là bao nhiêu?
$110$
$120$
$140$
$125$
Một buổi liên hoan ban tổ chức đã mua tất cả 840 cái bánh, 2352 cái kẹo và 560 quả quýt chia đều ra các đĩa, mỗi đĩa gồm cả bánh, kẹo và quýt. Tính số đĩa nhiều nhất mà ban tổ chức phải chuẩn bị?
$28$
$48$
$63$
$56$
Cho 2 số: $14n + 3$ và $21n + 4$ với $n$ là số tự nhiên, chọn đáp án đúng.
Hai số trên có hai ước chung
Hai số trên có ba ước chung
Hai số trên là hai số nguyên tố cùng nhau
Hai số trên chỉ có một ước chung là 3.
$BCNN(9;24)$ là bao nhiêu?
$54$
$18$
$72$
$36$
Đáp án : C
Bước 1 : Phân tích mỗi số ra thừa số nguyên tố.
Bước 2 : Chọn ra các thừa số nguyên tố chung và riêng.
Bước 3 : Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.
Ta có:
$\begin{array}{l}9 = {3^2};24 = {2^3}.3\\ \Rightarrow BCNN\left( {9;24} \right) = {2^3}{.3^2} = 8.9 = 72\end{array}$
Cho $36 = {2^2}{.3^2};60 = {2^2}.3.5;72 = {2^3}{.3^2}$. Ta có $ƯCLN(36;60;72)$là:
${2^3}.3.5$
${2^2}{.3^2}$
${2^2}.3$
$3.5$
Đáp án : C
Áp dụng phương pháp tìm ƯCLN: phân tích các số ra thừa số nguyên tố, chọn các thừa số chung. Mỗi thừa số lấy số mũ nhỏ nhất, tích của các số đó là ƯCLN
$36 = {2^2}{.3^2};60 = {2^2}.3.5;72 = {2^3}{.3^2}$
Ta số thừa số chung là $2;3$
Số mũ nhỏ nhất của $2$ là $2$; số mũ nhỏ nhất của $3$ là $1$
Vậy $ƯCLN\left( {36;60;72} \right) = {2^2}.3$.
Chọn câu đúng. $BCNN\left( {18;{\rm{ }}32;{\rm{ }}50} \right)$ là một số:
Có tổng các chữ số là $10$
Lẻ
Chia hết cho $10$
Có chữ số hàng đơn vị là $5$
Đáp án : C
Bước 1: Phân tích 18; 32 và 50 ra thừa số nguyên tố Bước 2: Chọn ra thừa số nguyên tố chung và riêng của 18; 32 và 50 Bước 3: Lập tích các thừa số nguyên tố đã chọn mỗi thừa số lấy với số mũ lớn nhất của nó Tích đó chính là $BCNN\left( {18;32;50} \right)$
Ta có \(18 = {2.3^2};32 = {2^5};50 = {2.5^2}\)
Nên \(BCNN\left( {18;32;50} \right) = {2^5}{.3^2}{.5^2} = 7200.\)
Vì $7200$ chia hết cho $10$ nên $C$ đúng.
Tìm số tự nhiên $a, b$ thỏa mãn $\overline {2a4b} $ chia hết cho các số $2; 3; 5$ và $9.$
$a = 3;b = 0$
$b = 3;a = 0$
$a = 1;b = 2$
$a = 9;b = 0$
Đáp án : A
Bước 1: Xác định b bằng tính chất: “ Một số chia hết cho $2$ và $5$ thì có chữ số tận cùng bằng $0$” Bước 2: Thay b vào rồi tính tổng các chữ số của $\overline {2a4b} $Để $\overline {2a4b} $ chia hết cho $3$ và $9$ thì tổng các chữ số phải chia hết cho $9$ Thử lần lượt các giá trị $a = 0,1,2,...,9$ vào xem giá trị nào thích hợp
Ta có: Để $\overline {2a4b} $ chia hết cho $2$ và $5$ thì $b = 0\;$ Thay $b = 0\;$ vào $\overline {2a4b} $ ta được $\overline {2a40} $ Tổng các chữ số là: \(2 + a + 4 + 0 = a + 6\) Thử lần lượt các giá trị $a = 0,1,2,...,9$Ta thấy với \(a = 3\) thì tổng các chữ số của $\overline {2a40} = 2340$ là: \(6 + 3 = 9\, \vdots \,9\)
Nên \(2340\) chia hết cho $3$ và $9$.
Vậy với \(a = 3;b = 0\) thì \(\overline {2a4b} \) chia hết cho \(2;3;5\) và \(9.\)
Tìm số tự nhiên a lớn nhất biết: $525\,\; \vdots \;\,a;{\rm{ }}875\;\, \vdots \;\,a;{\rm{ }}280\,\; \vdots \;\,a\;$
$125$
$25$
$175$
$35$
Đáp án : D
Ta đưa về bài toán tìm $ƯCLN$ của $525; 875; 280.$Bước 1: Phân tích $525; 875; 280$ ra thừa số nguyên tố.Bước 2: Chọn ra các thừa số nguyên tố chung.Bước 3: Lập tích các thừa số nguyên tố chung đó, mỗi thừa số lấy với số mũ nhỏ nhất của nó.Đó chính là số cần tìm.
Vì $525\,\; \vdots \;\,a;{\rm{ }}875\;\, \vdots \;\,a;{\rm{ }}280\,\; \vdots \;\,a\;$ và $a$ là số lớn nhất$ \Rightarrow a = ƯCLN\left( {525;{\rm{ }}875;{\rm{ }}280} \right)$ Ta có:

Nên \(525 = {3.5^2}.7;875 = {5^3}.7;280 = {2^3}.5.7\) $ \Rightarrow \;a = $ ƯCLN$\left( {525;875;280} \right) = 5.7 = 35\;$
Có bao nhiêu số tự nhiên \(x\) biết \(x \vdots 5;x \vdots 6\) và \(0 < x < 100\).
$1$
$2$
$5$
$3$
Đáp án : D
+ Tìm bội chung của \(5\) và \(6\)
+ Kết hợp với điều kiện \(0 < x < 100\) để tìm các số thỏa mãn.
Vì \(x \vdots 5;x \vdots 6\) nên \(x \in BC\left( {5;6} \right) = \left\{ {0;30;60;90;120;...} \right\}\)
Mà \(0 < x < 100\) nên \(x \in \left\{ {30;60;90} \right\}\).
Vậy \(x \in \left\{ {30;60;90} \right\}\).
Cho $A = 18 + 36 + 72 + 2x$. Tìm giá trị của $x$ biết rằng $A$ chia hết cho $9$ và $45 < x < 55$
$x = 45$
$x = 54$
A, B đều sai
A, B đều đúng
Đáp án : B
Áp dụng kiến thức về dấu hiệu chia hết:
Dấu hiệu chia hết cho $9$ là tổng tất cả các chữ số chia hết cho $9$
Dấu hiệu chia hết của $1$ tổng: nếu $a \vdots c;b \vdots c \Rightarrow (a + b) \vdots c$
Ta có $A = 18 + 36 + 72 + 2x$ mà $A \vdots 9;18 \vdots 9;36 \vdots 9;72 \vdots 9 \Rightarrow 2x \vdots 9 \Rightarrow x \vdots 9$
Mà $45 < x < 55 \Rightarrow x = 54$
Vậy $x = 54$.
Một trường học có khoảng từ 100 đến 150 học sinh khối 6. Khi xếp thành 10 hàng, 12 hàng, 15 hàng đều vừa đủ. Vậy hỏi số học sinh khối 6 của trường đó là bao nhiêu?
$110$
$120$
$140$
$125$
Đáp án : B
Áp dụng kiến thức về bội chung, nếu $a \vdots b;a \vdots c;a \vdots d$ thì $a$ là bội chung của $b,c,d$.
Từ đề bài suy ra số học sinh khối 6 là bội của 10;12;15.
Kết hợp điều kiện số học sinh trong khoảng từ 100 đến 150 để tìm số thích hợp
Gọi số học sinh khối 6 là \(x\left( {x \in {N^*}} \right)\) (học sinh)
Theo bài ra ta có:
\(x \vdots 10,x \vdots 12;x \vdots 15 \Rightarrow x \in BC\left( {10;12;15} \right)\) và \(100 \le x \le 150\).
Ta có
$\begin{array}{l}10 = 2.5;12 = {2^2}.3;15 = 3.5\\ \Rightarrow BCNN(10;12;15) = {2^2}.3.5 = 60\\ \Rightarrow BC\left( {10;12;15} \right) = \left\{ {0;60;120;180;...} \right\}\\ \Rightarrow x \in \left\{ {0;60;120;180;...} \right\} \end{array}$
Mà \(100 \le x \le 150\) nên \(x = 120\).
Vậy số học sinh khổi 6 là $120$ bạn.
Một buổi liên hoan ban tổ chức đã mua tất cả 840 cái bánh, 2352 cái kẹo và 560 quả quýt chia đều ra các đĩa, mỗi đĩa gồm cả bánh, kẹo và quýt. Tính số đĩa nhiều nhất mà ban tổ chức phải chuẩn bị?
$28$
$48$
$63$
$56$
Đáp án : D
Bước 1: Nếu gọi số đĩa là x cái, lập luận để có $x = $ƯCLN$\left( {840;2352;560} \right)$ Bước 2: Phân tích các số $840;{\rm{ }}2352;{\rm{ }}560$ ra thừa số nguyên tố Bước 3: Lập tích các thừa số nguyên tố chung, mỗi thừa số lấy với số mũ nhỏ nhất Đó chính là số đĩa cần tìm
Gọi số đĩa cần chẩn bị là x cái \(\left( {x \in {N^*}} \right)\) Vì số bánh, kẹo và quýt được chia đều vào các đĩa nên: $840\;\, \vdots x{\rm{ }};{\rm{ }}2352\,\; \vdots \;x{\rm{ }};{\rm{ }}560\;\, \vdots \;x$ Và $x$ là lớn nhất nên $x = $ƯCLN$\left( {840;2352;560} \right)$Ta có: \(840 = {2^3}.3.5.7;560 = {2^4}.5.7;2352 = {2^4}{.3.7^2}\)
Suy ra ƯCLN$\left( {840;{\rm{ }}2352;{\rm{ }}560} \right){\rm{ }} = \;{2^3}.7\; = 56$ Vậy số đĩa nhiều nhất cần chuẩn bị là $56$ .
Cho 2 số: $14n + 3$ và $21n + 4$ với $n$ là số tự nhiên, chọn đáp án đúng.
Hai số trên có hai ước chung
Hai số trên có ba ước chung
Hai số trên là hai số nguyên tố cùng nhau
Hai số trên chỉ có một ước chung là 3.
Đáp án : C
Dựa vào kiến thức 2 số nguyên tố cùng nhau là 2 số nguyên tố có ước chung lớn nhất là 1.
Áp dụng tính chất chia hết của 1 hiệu: Nếu $a \vdots c;b \vdots c \Rightarrow \left( {a - b} \right) \vdots c$
Gọi \(d = UCLN\left( {14n + 3;21n + 4} \right)\) ta có:
\(14n + 3\, \vdots \,d\) và \(21n + 4 \, \vdots \, d\)
\(3\left( {14n + 3} \right) \vdots \, d\) và \(2\left( {21n + 4} \right) \vdots d\)
\(42n + 9 \,\vdots \, d\) và \(42n + 8 \, \vdots \, d\)
\(\left( {42n + 9} \right) - \left( {42n + 8} \right) \vdots d\)
Suy ra \(1 \vdots d\)
\(d = 1\)
Vậy \(ƯCLN\left( {14n + 3;21n + 4} \right) = 1\) hay hai số đó là hai số nguyên tố cùng nhau.
Chương II Toán 6 Kết nối tri thức tập trung vào việc làm quen với số nguyên, các phép toán cơ bản trên số nguyên và ứng dụng của chúng trong giải quyết các bài toán thực tế. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương học tiếp theo. Bộ trắc nghiệm này được xây dựng nhằm giúp học sinh tự đánh giá năng lực, rà soát lại kiến thức và chuẩn bị tốt nhất cho các bài kiểm tra trên lớp.
Bộ trắc nghiệm bao gồm các dạng bài tập sau:
Việc luyện tập thường xuyên với các bài trắc nghiệm mang lại nhiều lợi ích:
Câu hỏi: Nhiệt độ tại đỉnh Fansipan vào buổi sáng là -3°C, đến buổi chiều nhiệt độ tăng lên 5°C. Hỏi nhiệt độ tại đỉnh Fansipan vào buổi chiều là bao nhiêu độ C?
A. 2°C
B. -8°C
C. 8°C
D. -2°C
Giải thích: Để tìm nhiệt độ buổi chiều, ta thực hiện phép cộng: -3 + 5 = 2. Vậy đáp án đúng là A. 2°C.
Hãy dành thời gian luyện tập đều đặn với bộ trắc nghiệm này. Đừng ngần ngại hỏi thầy cô hoặc bạn bè nếu gặp khó khăn. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
| Chủ đề | Nội dung chính |
|---|---|
| Số nguyên | Số tự nhiên, số nguyên âm, số nguyên dương, số 0 |
| So sánh số nguyên | Sử dụng dấu >, <, = để so sánh các số nguyên |
| Phép cộng, trừ số nguyên | Quy tắc cộng, trừ số nguyên dương, số nguyên âm |
| Phép nhân, chia số nguyên | Quy tắc nhân, chia số nguyên dương, số nguyên âm |