Bài viết này cung cấp bộ câu hỏi trắc nghiệm ôn tập và kiểm tra kiến thức về bài 21: Hình có trục đối xứng, chương trình Toán 6 Kết nối tri thức.
Các câu hỏi được thiết kế đa dạng, bao gồm nhiều mức độ khó, giúp học sinh rèn luyện kỹ năng nhận biết, phân tích và vận dụng kiến thức đã học.
Học sinh có thể sử dụng bộ trắc nghiệm này để tự đánh giá năng lực, chuẩn bị tốt nhất cho các bài kiểm tra trên lớp.
Trong những hình dưới đây, những hình có trục đối xứng là:
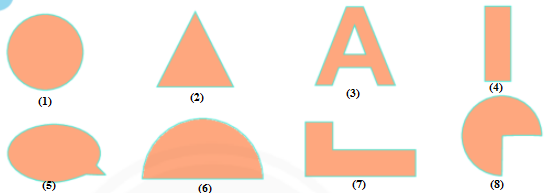
1,2,4
1,2,4,6
1,2,3,4,6,8
1,2,4,5
Hình chữ nhật có bao nhiêu trục đối xứng
1
2
3
4
Hình tam giác đều có mấy trục đối xứng:
1
2
3
0
Cho hai hình sau, chọn câu đúng:

Hình con sao biển có trục đối xứng
Hình chiếc lá có trục đối xứng
Hai hình đều có trục đối xứng.
Không có hình nào có trục đối xứng
Cho hình sau, chọn câu đúng nhất:
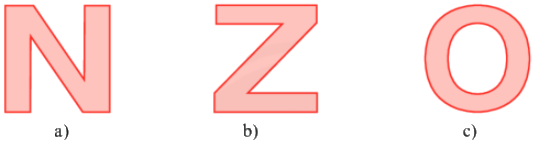
Hình a) và c) có trục đối xứng
Hình c) có trục đối xứng
Hình b) và c) có trục đối xứng
Cả 3 hình có trục đối xứng
Cho các hình sau, có bao nhiêu hình có trục đối xứng
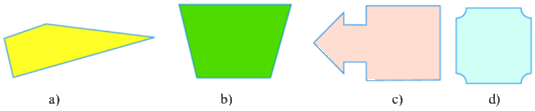
1
2
3
4
Trong các hình sau, hình nào có trục đối xứng?

hình a
hình b
hình a và hình b
không có hình nào
Cho các hình và các trục đối xứng của nó như hình dưới đây, hình vẽ có trục đối xứng đúng là:
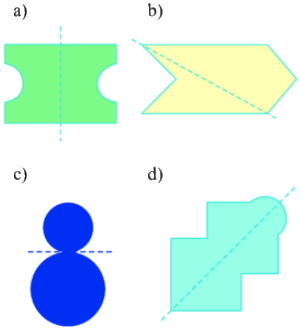
hình a
hình d
hình a và hình d
hình b và hình c
Hình nào sau đây có trục đối xứng?
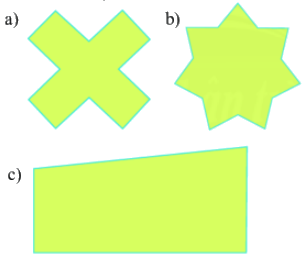
hình a
hình b
hình b và hình c
hình a và hình b
Hình sau có mấy trục đối xứng:
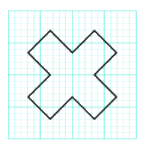
1
2
3
4
Lời giải và đáp án
Trong những hình dưới đây, những hình có trục đối xứng là:
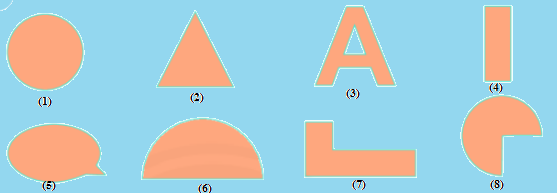
1,2,4
1,2,4,6
1,2,3,4,6,8
1,2,4,5
Đáp án : C
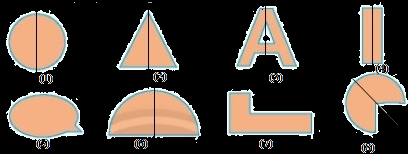
Vậy hình 1,2,3,4,6,8 là các hình có trục đối xứng.
Hình chữ nhật có bao nhiêu trục đối xứng
1
2
3
4
Đáp án : B
Trục đối xứng của hình chữ nhật là đường thẳng đi qua trung điểm hai đáy.

Vậy hình chữ nhật có 2 trục đối xứng.
Hình tam giác đều có mấy trục đối xứng:
1
2
3
0
Đáp án : C
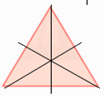
Vậy hình tam giác đều có 3 trục đối xứng.
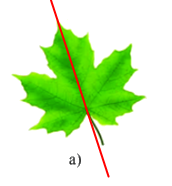
Cho hai hình sau, chọn câu đúng:

Hình con sao biển có trục đối xứng
Hình chiếc lá có trục đối xứng
Hai hình đều có trục đối xứng.
Không có hình nào có trục đối xứng
Đáp án : A

Vậy hình con sao biển có trục đối xứng.
Cho hình sau, chọn câu đúng nhất:
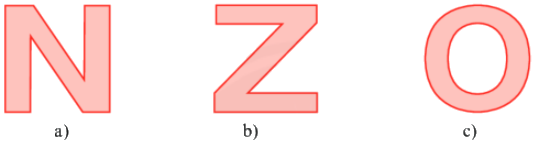
Hình a) và c) có trục đối xứng
Hình c) có trục đối xứng
Hình b) và c) có trục đối xứng
Cả 3 hình có trục đối xứng
Đáp án : B
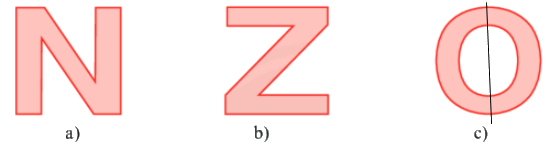
Ta có chữ N và Z không có trục đối xứng, chữ O có trục đối xứng.
Vậy hình c) có trục đối xứng.
Cho các hình sau, có bao nhiêu hình có trục đối xứng
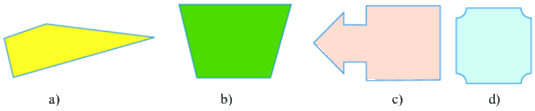
1
2
3
4
Đáp án : C
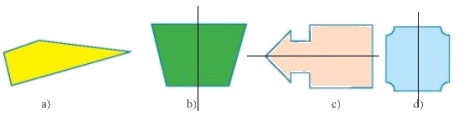
=> Các hình có trục đối xứng là: b, c, d.
Vậy có 3 hình có trục đối xứng.
Trong các hình sau, hình nào có trục đối xứng?

hình a
hình b
hình a và hình b
không có hình nào
Đáp án : A
Hình a có trục đối xứng.
Cho các hình và các trục đối xứng của nó như hình dưới đây, hình vẽ có trục đối xứng đúng là:
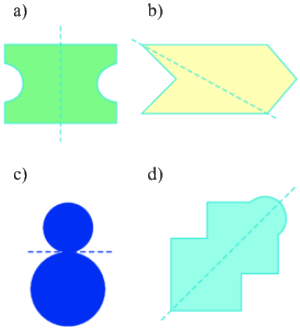
hình a
hình d
hình a và hình d
hình b và hình c
Đáp án : C
Đường nét đứt ở hình a và d là trục đối xứng. Hai đường ở hình b và c còn lại không phải là trục đối xứng của hình
Hình nào sau đây có trục đối xứng?
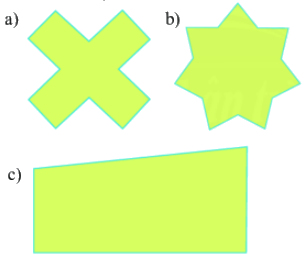
hình a
hình b
hình b và hình c
hình a và hình b
Đáp án : D
Hình a và hình b có trục đối xứng, ví dụ ta có thể vẽ trục đối xứng của chúng như sau:
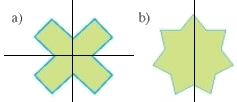
Hình sau có mấy trục đối xứng:
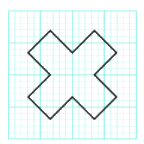
1
2
3
4
Đáp án : D
Ta vẽ các trục đối xứng của hình như sau:
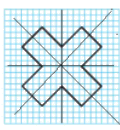
Vậy hình đã cho có 4 trục đối xứng.
Trong chương trình Toán 6 Kết nối tri thức, bài 21 tập trung vào việc giới thiệu khái niệm về trục đối xứng và cách nhận biết các hình có trục đối xứng. Hiểu rõ khái niệm này là nền tảng quan trọng để học tập các kiến thức hình học nâng cao hơn.
Một hình được gọi là có trục đối xứng nếu có một đường thẳng (trục đối xứng) sao cho khi gấp hình theo đường thẳng đó, hai phần của hình trùng khít lên nhau. Trục đối xứng thường là đường thẳng đi qua tâm của hình.
Để nhận biết một hình có trục đối xứng, ta có thể thực hiện các bước sau:
Dưới đây là một số câu hỏi trắc nghiệm minh họa để giúp bạn hiểu rõ hơn về bài học:
Đáp án: c. Hình chữ nhật
Đáp án: d. 4
Đáp án: c. Tam giác vuông cân
Kiến thức về trục đối xứng có nhiều ứng dụng trong thực tế, chẳng hạn như trong thiết kế, kiến trúc, nghệ thuật và các lĩnh vực khoa học khác. Ví dụ, các họa tiết trang trí thường được thiết kế dựa trên nguyên tắc đối xứng để tạo ra sự hài hòa và cân đối.
Để nắm vững kiến thức về bài 21, bạn nên luyện tập thêm các bài tập trắc nghiệm và bài tập tự luận khác. Hãy tìm kiếm các tài liệu học tập trên internet hoặc trong sách giáo khoa để có thêm nhiều bài tập thực hành.
Bài 21: Hình có trục đối xứng là một bài học quan trọng trong chương trình Toán 6 Kết nối tri thức. Việc hiểu rõ khái niệm và các tính chất của trục đối xứng sẽ giúp bạn học tốt môn Toán và ứng dụng kiến thức vào thực tế.
| Hình | Số trục đối xứng |
|---|---|
| Hình vuông | 4 |
| Hình chữ nhật | 2 |
| Hình thoi | 2 |
| Hình tròn | Vô số |
| Bảng tổng hợp số trục đối xứng của một số hình | |