Bài viết này cung cấp bộ câu hỏi trắc nghiệm giúp học sinh lớp 6 ôn tập và đánh giá kiến thức về các hình đa giác đều: hình tam giác đều, hình vuông và hình lục giác đều.
Các câu hỏi được thiết kế bám sát chương trình Kết nối tri thức, đa dạng về mức độ từ dễ đến khó, giúp học sinh rèn luyện kỹ năng giải quyết vấn đề và áp dụng kiến thức vào thực tế.
Cho hình vuông \(MNPQ\), khẳng định nào sau đây sai?
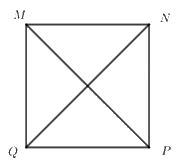
\(MQ = QP\)
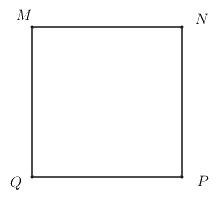
Cho hình vuông \(MNPQ\), khẳng định nào sau đây đúng?
Chọn phát biểu sai?
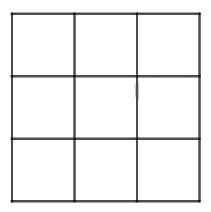
Hình dưới đây có tất cả bao nhiêu hình vuông?
Phát biểu nào sau đây sai?
Hình lục giác đều có 6 đỉnh
Hình lục giác đều có 6 cạnh
Hình lục giác đều có 6 đường chéo chính
Hình lục giác đều có 6 góc
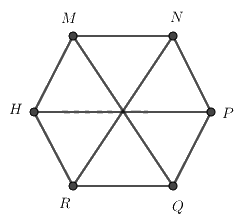
Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
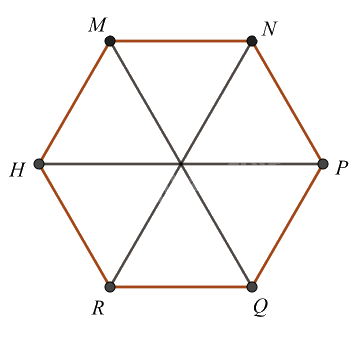
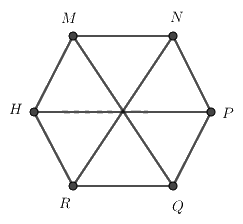
Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Chọn phát biểu sai:
Tam giác đều có ba cạnh
Cho tam giác đều \(MNP\) có \(MN = 5\,cm\), khẳng định nào sau đây đúng?
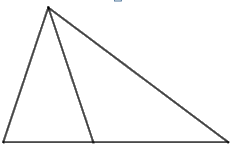
Hình dưới đây có mấy hình tam giác?
Lời giải và đáp án
Cho hình vuông \(MNPQ\), khẳng định nào sau đây sai?
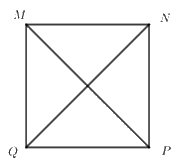
\(MQ = QP\)
Đáp án : D
Trong hình vuông:
- Bốn cạnh bằng nhau.
- Hai đường chéo bằng nhau.
Hình vuông \(MNPQ\) có: \(MN = NP = PQ = MQ\)
=> Đáp án A, B, C đúng.
Đáp án D sai do \(MN\) là cạnh của hình vuông, \(MP\) là đường chéo nên \(MN = MP\) là sai.
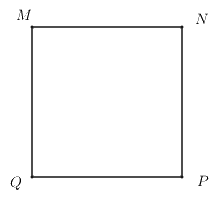
Cho hình vuông \(MNPQ\), khẳng định nào sau đây đúng?
Đáp án : A
Trong hình vuông, hai cặp cạnh đối song song với nhau.
Trong hình vuông \(MNPQ\) có hai cặp cạnh đối song song với nhau là:
+ \(MN\) và \(PQ\).
+ \(MQ\) và \(NP\)
=> Đáp án A đúng.
Chọn phát biểu sai?
Đáp án : B
Sử dụng dấu hiệu nhận biết của hình vuông.
Hình vuông có hai cặp cạnh đối song song => Đáp án B sai.
Hình dưới đây có tất cả bao nhiêu hình vuông?
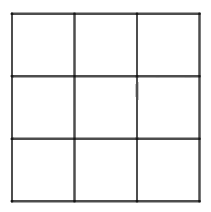
Đáp án : B
Đếm số hình vuông nhỏ + số hình vuông được ghép từ các ô vuông nhỏ.
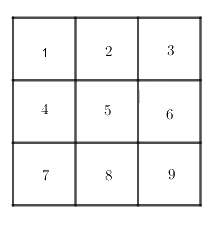
Ta đánh số như hình trên:
+ 9 hình vuông nhỏ là: 1, 2, 3, 4, 5, 6, 7, 8, 9.
+ 4 hình vuông được gép từ bốn hình vuông nhỏ là: 1245, 2356, 4578, 5689.
+ 1 hình vuông lớn được ghép từ 9 hình vuông nhỏ.
Vậy có tất cả \(9 + 4 + 1 = 14\) hình vuông.
Phát biểu nào sau đây sai?
Hình lục giác đều có 6 đỉnh
Hình lục giác đều có 6 cạnh
Hình lục giác đều có 6 đường chéo chính
Hình lục giác đều có 6 góc
Đáp án : C
Sử dụng dấu hiệu nhận biết lục giác đều.
Các đáp án A, B, D đúng.
Hình lục giác đều có 3 đường chéo chính => Đáp án C sai.
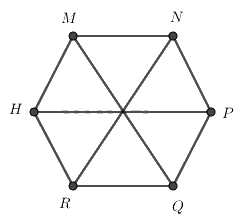
Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Đáp án : D
- Trong hình lục giác đều:
+ 6 cạnh bằng nhau
+ 3 đường chéo chính bằng nhau.
Hình lục giác đều MNPQRH có 3 đường chéo chính bằng nhau nên: \(MQ = NR\)
=> A đúng
Hình lục giác đều MNPQRH có 6 cạnh bằng nhau nên \(MH = RQ\) và \(MN = HR\)
=> B, C đúng.
Do MH là cạnh, MQ là đường chéo chính nên hai đoạn này không bằng nhau
=> D sai
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
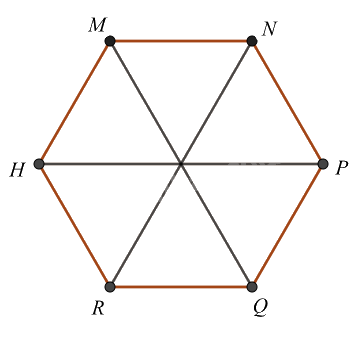
Đáp án : D
Đếm số tam giác đều đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
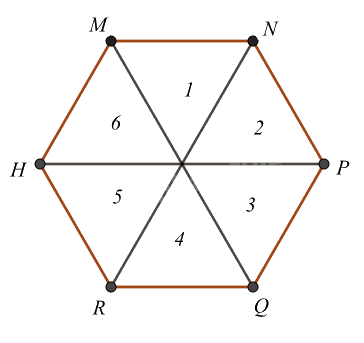
Ta đánh số như hình trên
Hình lục giác đều được tạo thành bởi 6 hình tam giác đều nên các hình tam giác đều là: 1, 2, 3, 4, 5, 6.
Vậy có 6 tam giác đều.
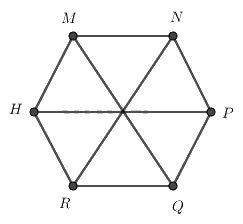
Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Đáp án : B
- Trong hình lục giác đều:
+ 6 cạnh bằng nhau
+ 3 đường chéo chính bằng nhau.
Đáp án B sai do MQ là đường chéo chính, sửa lại:
6 cạnh là MN, NP, PQ, HR, QR, HM
Chọn phát biểu sai:
Tam giác đều có ba cạnh
Đáp án : C
Trong tam giác đều ba góc bằng nhau => Đáp án C sai.
Cho tam giác đều \(MNP\) có \(MN = 5\,cm\), khẳng định nào sau đây đúng?
Đáp án : D
Trong tam giác đều ba cạnh bằng nhau mà \(MN = 5\,cm\) nên ta có: \(MN = NP = MP = 5\,cm\)
=> Chọn D
Hình dưới đây có mấy hình tam giác?
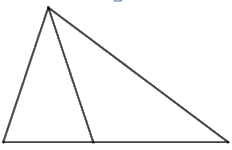
Đáp án : C
Đếm số hình tam giác nhỏ + số hình tam giác tạo từ các hình tam giác nhỏ
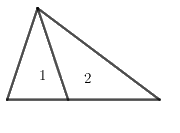
Hình trên có 2 hình tam giác nhỏ là: 1, 2 và 1 hình tam giác lớn ghép từ hai hình trên
=> Có tất cả 3 hình tam giác
Cho hình vuông \(MNPQ\), khẳng định nào sau đây sai?

\(MQ = QP\)

Cho hình vuông \(MNPQ\), khẳng định nào sau đây đúng?
Chọn phát biểu sai?
Hình dưới đây có tất cả bao nhiêu hình vuông?

Phát biểu nào sau đây sai?
Hình lục giác đều có 6 đỉnh
Hình lục giác đều có 6 cạnh
Hình lục giác đều có 6 đường chéo chính
Hình lục giác đều có 6 góc

Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều


Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Chọn phát biểu sai:
Tam giác đều có ba cạnh
Cho tam giác đều \(MNP\) có \(MN = 5\,cm\), khẳng định nào sau đây đúng?
Hình dưới đây có mấy hình tam giác?

Cho hình vuông \(MNPQ\), khẳng định nào sau đây sai?

\(MQ = QP\)
Đáp án : D
Trong hình vuông:
- Bốn cạnh bằng nhau.
- Hai đường chéo bằng nhau.
Hình vuông \(MNPQ\) có: \(MN = NP = PQ = MQ\)
=> Đáp án A, B, C đúng.
Đáp án D sai do \(MN\) là cạnh của hình vuông, \(MP\) là đường chéo nên \(MN = MP\) là sai.

Cho hình vuông \(MNPQ\), khẳng định nào sau đây đúng?
Đáp án : A
Trong hình vuông, hai cặp cạnh đối song song với nhau.
Trong hình vuông \(MNPQ\) có hai cặp cạnh đối song song với nhau là:
+ \(MN\) và \(PQ\).
+ \(MQ\) và \(NP\)
=> Đáp án A đúng.
Chọn phát biểu sai?
Đáp án : B
Sử dụng dấu hiệu nhận biết của hình vuông.
Hình vuông có hai cặp cạnh đối song song => Đáp án B sai.
Hình dưới đây có tất cả bao nhiêu hình vuông?

Đáp án : B
Đếm số hình vuông nhỏ + số hình vuông được ghép từ các ô vuông nhỏ.

Ta đánh số như hình trên:
+ 9 hình vuông nhỏ là: 1, 2, 3, 4, 5, 6, 7, 8, 9.
+ 4 hình vuông được gép từ bốn hình vuông nhỏ là: 1245, 2356, 4578, 5689.
+ 1 hình vuông lớn được ghép từ 9 hình vuông nhỏ.
Vậy có tất cả \(9 + 4 + 1 = 14\) hình vuông.
Phát biểu nào sau đây sai?
Hình lục giác đều có 6 đỉnh
Hình lục giác đều có 6 cạnh
Hình lục giác đều có 6 đường chéo chính
Hình lục giác đều có 6 góc
Đáp án : C
Sử dụng dấu hiệu nhận biết lục giác đều.
Các đáp án A, B, D đúng.
Hình lục giác đều có 3 đường chéo chính => Đáp án C sai.

Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Đáp án : D
- Trong hình lục giác đều:
+ 6 cạnh bằng nhau
+ 3 đường chéo chính bằng nhau.
Hình lục giác đều MNPQRH có 3 đường chéo chính bằng nhau nên: \(MQ = NR\)
=> A đúng
Hình lục giác đều MNPQRH có 6 cạnh bằng nhau nên \(MH = RQ\) và \(MN = HR\)
=> B, C đúng.
Do MH là cạnh, MQ là đường chéo chính nên hai đoạn này không bằng nhau
=> D sai
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều

Đáp án : D
Đếm số tam giác đều đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều

Ta đánh số như hình trên
Hình lục giác đều được tạo thành bởi 6 hình tam giác đều nên các hình tam giác đều là: 1, 2, 3, 4, 5, 6.
Vậy có 6 tam giác đều.

Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Đáp án : B
- Trong hình lục giác đều:
+ 6 cạnh bằng nhau
+ 3 đường chéo chính bằng nhau.
Đáp án B sai do MQ là đường chéo chính, sửa lại:
6 cạnh là MN, NP, PQ, HR, QR, HM
Chọn phát biểu sai:
Tam giác đều có ba cạnh
Đáp án : C
Trong tam giác đều ba góc bằng nhau => Đáp án C sai.
Cho tam giác đều \(MNP\) có \(MN = 5\,cm\), khẳng định nào sau đây đúng?
Đáp án : D
Trong tam giác đều ba cạnh bằng nhau mà \(MN = 5\,cm\) nên ta có: \(MN = NP = MP = 5\,cm\)
=> Chọn D
Hình dưới đây có mấy hình tam giác?

Đáp án : C
Đếm số hình tam giác nhỏ + số hình tam giác tạo từ các hình tam giác nhỏ

Hình trên có 2 hình tam giác nhỏ là: 1, 2 và 1 hình tam giác lớn ghép từ hai hình trên
=> Có tất cả 3 hình tam giác
Bài 18 chương trình Toán 6 Kết nối tri thức tập trung vào việc nghiên cứu các hình đa giác đều, cụ thể là hình tam giác đều, hình vuông và hình lục giác đều. Việc nắm vững các tính chất và công thức liên quan đến các hình này là vô cùng quan trọng, không chỉ cho việc giải các bài tập trong sách giáo khoa mà còn là nền tảng cho các kiến thức hình học nâng cao hơn.
Hình tam giác đều là hình tam giác có ba cạnh bằng nhau và ba góc bằng nhau (đều bằng 60 độ). Các tính chất quan trọng của hình tam giác đều bao gồm:
Công thức tính diện tích hình tam giác đều với cạnh a là: Diện tích = (a2√3)/4
Hình vuông là hình có bốn cạnh bằng nhau và bốn góc vuông. Các tính chất quan trọng của hình vuông bao gồm:
Công thức tính diện tích hình vuông với cạnh a là: Diện tích = a2
Công thức tính chu vi hình vuông với cạnh a là: Chu vi = 4a
Hình lục giác đều là hình có sáu cạnh bằng nhau và sáu góc bằng nhau (đều bằng 120 độ). Các tính chất quan trọng của hình lục giác đều bao gồm:
Công thức tính diện tích hình lục giác đều với cạnh a là: Diện tích = (3√3a2)/2
Câu 1: Hình nào sau đây là hình tam giác đều?
Câu 2: Diện tích của hình vuông có cạnh 5cm là bao nhiêu?
Câu 3: Một hình lục giác đều có cạnh 4cm. Chu vi của hình lục giác đều đó là bao nhiêu?
Việc luyện tập thường xuyên với các bài tập trắc nghiệm sẽ giúp học sinh nắm vững kiến thức và tự tin hơn khi làm bài kiểm tra.