Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Trong bài viết này, chúng tôi sẽ cùng nhau giải quyết các bài tập trong mục 5 trang 53 và 54 của Chuyên đề học tập Toán 10 - Cánh diều.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong quá trình học tập.
Cho hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\).
Viết phương trình chình tắc của đườn hypebol biết một tiêu điểm là \({F_2}(\sqrt 2 ;0)\) và đường chuẩn ứng với tiêu điểm đó là: \(x = \frac{1}{{\sqrt 2 }}\).
Phương pháp giải:
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\). Khi đó ta có:
+ Tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\)
+ Ứng với tiêu điểm \({F_1}( - c;0)\), có đường chuẩn \({\Delta _1}:x + \frac{a}{e} = 0\)
+ Ứng với tiêu điểm \({F_2}(c;0)\), có đường chuẩn \({\Delta _2}:x - \frac{a}{e} = 0\)
Lời giải chi tiết:
Gọi phương trình chính tắc của hypebol là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) (\(a > 0,b > 0\)).
+ Tiêu điểm \({F_2}(c;0) = (\sqrt 2 ;0) \Rightarrow c = \sqrt 2 \)
+ Ứng với tiêu điểm \({F_2}(c;0)\), có đường chuẩn \({\Delta _2}:x = \frac{a}{e}\) hay \(\frac{a}{e} = \frac{1}{{\sqrt 2 }}\)
Mà \(e = \frac{c}{a} \Rightarrow \frac{a}{e} = \frac{{{a^2}}}{c} = \frac{{{a^2}}}{{\sqrt 2 }} \Rightarrow {a^2} = 1 \Rightarrow a = 1.\) Suy ra \(b = \sqrt {{c^2} - {a^2}} = 1\)
Vậy PTCT của hypebol là \({x^2} - {y^2} = 1\)
Cho hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\).
Xét đường thẳng \({\Delta _1}:x = - \frac{a}{e}\) với mỗi điểm \(M\left( {{x_0};{y_0}} \right) \in \left( H \right)\) (Hình 17), tính:
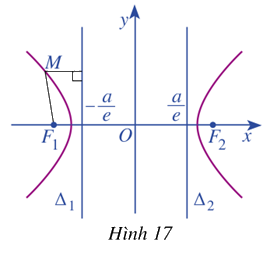
a) Khoảng cách \(d\left( {M,{\Delta _1}} \right)\) từ điểm \(M\left( {{x_0};{y_0}} \right)\) đến đường thẳng \({\Delta _1}\)
b) Tỉ số \(\frac{{M{F_1}}}{{d\left( {M,{\Delta _1}} \right)}}\)
Lời giải chi tiết:
a) Viết lại phương trình đưởng thẳng \({\Delta _1}\) ở dạng: \(x + 0y + \frac{a}{e} = 0\)
Với mỗi điểm \(M\left( {{x_0};{y_0}} \right) \in \left( H \right)\), ta có: \(d\left( {M,{\Delta _1}} \right) = \frac{{\left| {x + 0y + \frac{a}{e}} \right|}}{{\sqrt {{1^2} + {0^2}} }} = \left| {x + \frac{a}{e}} \right| = \frac{{\left| {a + ex} \right|}}{e}\)
b) Ta có: \(M{F_1} = \left| {a + ex} \right| \Rightarrow \frac{{M{F_1}}}{{d\left( {M,{\Delta _1}} \right)}} = \frac{{\left| {a + ex} \right|}}{{\frac{{\left| {a + ex} \right|}}{e}}} = e\)
Vậy \(\frac{{M{F_1}}}{{d\left( {M,{\Delta _1}} \right)}} = e\)
Cho hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\).
Xét đường thẳng \({\Delta _1}:x = - \frac{a}{e}\) với mỗi điểm \(M\left( {{x_0};{y_0}} \right) \in \left( H \right)\) (Hình 17), tính:
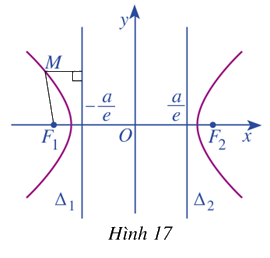
a) Khoảng cách \(d\left( {M,{\Delta _1}} \right)\) từ điểm \(M\left( {{x_0};{y_0}} \right)\) đến đường thẳng \({\Delta _1}\)
b) Tỉ số \(\frac{{M{F_1}}}{{d\left( {M,{\Delta _1}} \right)}}\)
Lời giải chi tiết:
a) Viết lại phương trình đưởng thẳng \({\Delta _1}\) ở dạng: \(x + 0y + \frac{a}{e} = 0\)
Với mỗi điểm \(M\left( {{x_0};{y_0}} \right) \in \left( H \right)\), ta có: \(d\left( {M,{\Delta _1}} \right) = \frac{{\left| {x + 0y + \frac{a}{e}} \right|}}{{\sqrt {{1^2} + {0^2}} }} = \left| {x + \frac{a}{e}} \right| = \frac{{\left| {a + ex} \right|}}{e}\)
b) Ta có: \(M{F_1} = \left| {a + ex} \right| \Rightarrow \frac{{M{F_1}}}{{d\left( {M,{\Delta _1}} \right)}} = \frac{{\left| {a + ex} \right|}}{{\frac{{\left| {a + ex} \right|}}{e}}} = e\)
Vậy \(\frac{{M{F_1}}}{{d\left( {M,{\Delta _1}} \right)}} = e\)
Viết phương trình chình tắc của đườn hypebol biết một tiêu điểm là \({F_2}(\sqrt 2 ;0)\) và đường chuẩn ứng với tiêu điểm đó là: \(x = \frac{1}{{\sqrt 2 }}\).
Phương pháp giải:
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\). Khi đó ta có:
+ Tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\)
+ Ứng với tiêu điểm \({F_1}( - c;0)\), có đường chuẩn \({\Delta _1}:x + \frac{a}{e} = 0\)
+ Ứng với tiêu điểm \({F_2}(c;0)\), có đường chuẩn \({\Delta _2}:x - \frac{a}{e} = 0\)
Lời giải chi tiết:
Gọi phương trình chính tắc của hypebol là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) (\(a > 0,b > 0\)).
+ Tiêu điểm \({F_2}(c;0) = (\sqrt 2 ;0) \Rightarrow c = \sqrt 2 \)
+ Ứng với tiêu điểm \({F_2}(c;0)\), có đường chuẩn \({\Delta _2}:x = \frac{a}{e}\) hay \(\frac{a}{e} = \frac{1}{{\sqrt 2 }}\)
Mà \(e = \frac{c}{a} \Rightarrow \frac{a}{e} = \frac{{{a^2}}}{c} = \frac{{{a^2}}}{{\sqrt 2 }} \Rightarrow {a^2} = 1 \Rightarrow a = 1.\) Suy ra \(b = \sqrt {{c^2} - {a^2}} = 1\)
Vậy PTCT của hypebol là \({x^2} - {y^2} = 1\)
Mục 5 của Chuyên đề học tập Toán 10 - Cánh diều tập trung vào việc ứng dụng các kiến thức về vectơ trong không gian để giải quyết các bài toán hình học. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các công thức tính độ dài vectơ, tích vô hướng, và các tính chất của vectơ để chứng minh các đẳng thức, tính góc, và xác định vị trí tương đối của các điểm trong không gian.
Bài tập này yêu cầu học sinh tính độ dài của các vectơ cho trước. Để giải bài tập này, học sinh cần nắm vững công thức tính độ dài vectơ: |a| = √(x² + y² + z²), trong đó a = (x, y, z).
Ví dụ: Cho vectơ a = (1, 2, 3). Tính độ dài của vectơ a.
Giải:
|a| = √(1² + 2² + 3²) = √(1 + 4 + 9) = √14
Bài tập này yêu cầu học sinh tính tích vô hướng của hai vectơ. Để giải bài tập này, học sinh cần nắm vững công thức tính tích vô hướng: a.b = x₁x₂ + y₁y₂ + z₁z₂, trong đó a = (x₁, y₁, z₁) và b = (x₂, y₂, z₂).
Ví dụ: Cho vectơ a = (1, 2, 3) và b = (4, 5, 6). Tính tích vô hướng của hai vectơ a và b.
Giải:
a.b = 1*4 + 2*5 + 3*6 = 4 + 10 + 18 = 32
Bài tập này yêu cầu học sinh chứng minh một đẳng thức vectơ. Để giải bài tập này, học sinh cần sử dụng các tính chất của vectơ, như tính chất giao hoán, tính chất kết hợp, tính chất phân phối, và các công thức liên quan đến tích vô hướng.
Ví dụ: Chứng minh rằng (a + b) . c = a.c + b.c với mọi vectơ a, b, c.
Giải:
(a + b) . c = (a₁ + b₁, a₂ + b₂, a₃ + b₃) . (c₁, c₂, c₃) = (a₁c₁ + a₂c₂ + a₃c₃) + (b₁c₁ + b₂c₂ + b₃c₃) = a.c + b.c
Bài tập này yêu cầu học sinh tính góc giữa hai vectơ. Để giải bài tập này, học sinh cần sử dụng công thức tính cosin góc giữa hai vectơ: cos(θ) = (a.b) / (|a| * |b|), trong đó θ là góc giữa hai vectơ a và b.
Ví dụ: Cho vectơ a = (1, 0, 0) và b = (0, 1, 0). Tính góc giữa hai vectơ a và b.
Giải:
a.b = 1*0 + 0*1 + 0*0 = 0
|a| = √(1² + 0² + 0²) = 1
|b| = √(0² + 1² + 0²) = 1
cos(θ) = 0 / (1 * 1) = 0
θ = 90°
Bài tập này yêu cầu học sinh xác định vị trí tương đối của các điểm trong không gian. Để giải bài tập này, học sinh cần sử dụng các công thức tính khoảng cách giữa hai điểm, tích vô hướng, và các tính chất của vectơ.
Ví dụ: Cho ba điểm A(1, 2, 3), B(4, 5, 6), và C(7, 8, 9). Xác định xem ba điểm A, B, C có thẳng hàng hay không.
Giải:
Vectơ AB = (4-1, 5-2, 6-3) = (3, 3, 3)
Vectơ AC = (7-1, 8-2, 9-3) = (6, 6, 6)
Ta thấy rằng vectơ AC = 2 * vectơ AB, do đó ba điểm A, B, C thẳng hàng.
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, bạn đã có thể tự tin giải quyết các bài tập trong mục 5 trang 53, 54 của Chuyên đề học tập Toán 10 - Cánh diều. Chúc bạn học tập tốt!