Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 3 trang 67 Chuyên đề học tập Toán 10 – Cánh diều. Bài viết này sẽ cung cấp cho bạn các bước giải bài tập một cách rõ ràng, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, chính xác và cập nhật mới nhất để hỗ trợ tối đa cho học sinh, sinh viên và những người yêu thích môn Toán.
Cho parabol có phương trình chính tắc \({y^2} = 2x\). Tìm tiêu điểm, phương trình đường chuẩn của parabol và vẽ parabol đó.
Đề bài
Cho parabol có phương trình chính tắc \({y^2} = 2x\). Tìm tiêu điểm, phương trình đường chuẩn của parabol và vẽ parabol đó.
Phương pháp giải - Xem chi tiết
Cho parabol có PTCT: \({y^2} = 2px\) trong đó \(p > 0\)
+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)
+ Đường chuẩn: \(\Delta :x = - \frac{p}{2}\)
Lời giải chi tiết
+ Ta có: \(2p = 2 \Rightarrow p = 1\)
Tiêu điểm của parabol (P) là \(F\left( {\frac{1}{2};0} \right)\)
Đường chuẩn: \(\Delta :x = - \frac{1}{2}\)
+ Vẽ parabol
Để vẽ parabol (P): \({y^2} = 2x\) ta có thể làm như sau:
Bước 1: Lập bảng giá trị
x | 0 | 0,5 | 0,5 | 2 | 2 | 4,5 | 4,5 |
y | 0 | -1 | 1 | -2 | 2 | -3 | 3 |
Chú ý rằng tương ứng với mỗi giá trị dương của x có hai giá trị của y đối nhau
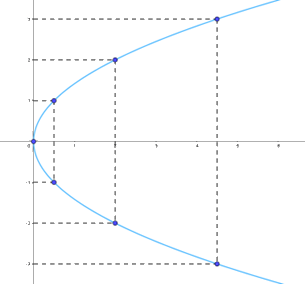
Bước 2: Vẽ các điểm cụ thể mà hoành độ và tung độ được xác định như trong bảng giá trị
Bước 3: Vẽ đường parabol bên phải trục Oy, đỉnh O, trục đối xứng là Ox, parabol đi qua các điểm được vẽ ở Bước 2
Bài 3 trang 67 Chuyên đề học tập Toán 10 – Cánh diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ, phép toán vectơ và ứng dụng của vectơ trong hình học. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm cơ bản, nắm vững các công thức và kỹ năng giải toán liên quan.
Bài 3 trang 67 thường bao gồm các dạng bài tập sau:
Để giúp các bạn học sinh giải quyết bài tập một cách hiệu quả, Giaitoan.edu.vn xin trình bày lời giải chi tiết cho từng phần của bài 3 trang 67:
Đề bài: Cho hai vectơ a = (1; 2) và b = (-3; 4). Tính a + b.
Lời giải:
a + b = (1 + (-3); 2 + 4) = (-2; 6)
Đề bài: Cho vectơ a = (2; -1) và số thực k = 3. Tính ka.
Lời giải:
ka = 3(2; -1) = (3*2; 3*(-1)) = (6; -3)
Đề bài: Cho ba điểm A(1; 2), B(3; 4), C(5; 6). Chứng minh A, B, C thẳng hàng.
Lời giải:
Ta có vectơ AB = (3-1; 4-2) = (2; 2) và vectơ AC = (5-1; 6-2) = (4; 4).
Vì AC = 2AB nên vectơ AC và AB cùng phương. Hơn nữa, A là điểm chung của hai vectơ nên A, B, C thẳng hàng.
Để củng cố kiến thức và kỹ năng giải toán, các bạn có thể tự giải các bài tập tương tự với các số liệu khác nhau. Ngoài ra, hãy tham khảo thêm các tài liệu học tập, sách giáo khoa và các trang web học toán uy tín để nâng cao trình độ.
Khi giải bài tập về vectơ, cần lưu ý những điều sau:
Bài 3 trang 67 Chuyên đề học tập Toán 10 – Cánh diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về vectơ. Hy vọng với lời giải chi tiết và những lưu ý trên, các bạn sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.