Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 4 trang 43, 44, 45 Chuyên đề học tập Toán 10 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán.
Chuyên đề học tập Toán 10 - Cánh diều là một tài liệu quan trọng, hỗ trợ các em ôn luyện và củng cố kiến thức.
Giả sử đường elip (E) là tập hợp các điểm M trong mặt phẳng sao cho \(M{F_1} + M{F_2} = 2a\), ở đó \({F_1}{F_2} = 2c\) với \(0 < c < a\).
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\). Giả sử M là điểm thuộc elip và có hoành độ là 2. Tìm độ dài của các bán kính qua tiêu của điểm M.
Phương pháp giải:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
+ Độ dài bán kính qua tiêu của điểm \(M(x,y)\) trên (E) là: \(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x.\)
Lời giải chi tiết:
Ta có \(c = \sqrt {{a^2} - {b^2}} = \sqrt {25 - 9} = 4\). Do đó \(e = \frac{c}{a} = \frac{4}{5} = 0,8\). Vậy độ dài các bán kính qua tiêu của điểm M là:
\(M{F_1} = a + \frac{c}{a}x = 5 + 0,8.2 = 6,6;M{F_2} = a - \frac{c}{a}x = 5 - 0,8.2 = 3,4\)
Sử dụng đẳng thức c) ở trên và đẳng thức \(M{F_1} + M{F_2} = 2a\), chứng minh:
a) \(M{F_1} - M{F_2} = \frac{{2c}}{a}x\)
b) \(M{F_1} = a + \frac{c}{a}x\)
c) \(M{F_2} = a - \frac{c}{a}x\)
Lời giải chi tiết:
a) Ta có: \(M{F_1}^2 - M{F_2}^2 = \left( {M{F_1} - M{F_2}} \right)\left( {M{F_1} + M{F_2}} \right) = \left( {M{F_1} - M{F_2}} \right).2a = 4cx\)
\( \Rightarrow M{F_1} - M{F_2} = \frac{{2c}}{a}x\)
b) Ta có: \(\left\{ \begin{array}{l}M{F_1} + M{F_2} = 2a\left( 1 \right)\\M{F_1} - M{F_2} = \frac{{2c}}{a}x\left( 2 \right)\end{array} \right.\)
Cộng hai vế của (1) và (2) ta được: \(2M{F_1} = 2a + \frac{{2c}}{a}x \Rightarrow M{F_1} = a + \frac{c}{a}x\)
c) Ta có: \(M{F_2} = 2a - M{F_1} = 2a - \left( {a + \frac{c}{a}x} \right) = a - \frac{c}{a}x\)
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\). Giả sử \(M\left( {x;y} \right)\) là điểm thuộc elip. Tìm giá trị lớn nhất và bé nhất của bán kính qua tiêu \(M{F_1}\) và \(M{F_2}\)
Phương pháp giải:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
+ Độ dài bán kính qua tiêu của điểm \(M(x,y)\) trên (E) là: \(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x.\)
\(M{F_1}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = - a\) và có giá trị lớn nhất là \(a + c\) khi \(x = a\)
\(M{F_2}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = a\) và có giá trị lớn nhất là \(a + c\) khi \(x = - a\)
Lời giải chi tiết:
Vì \( - a \le x \le a\) nên \(a + \frac{c}{a}\left( { - a} \right) \le a + \frac{c}{a}x \le a + \frac{c}{a}\left( a \right) \Leftrightarrow a - c \le M{F_1} \le a + c\)
Vậy \(M{F_1}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = - a\) và có giá trị lớn nhất là \(a + c\) khi \(x = a\)
Tương tự với \(M{F_2}\), ta có \( - a \le x \le a \Rightarrow a \ge - x \ge - a\) hay \( - a \le x \le a\) nên \(a - \frac{c}{a}\left( a \right) \le a - \frac{c}{a}x \le a - \frac{c}{a}\left( { - a} \right) \Leftrightarrow a - c \le M{F_2} \le a + c\)
Vậy \(M{F_2}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = a\) và có giá trị lớn nhất là \(a + c\) khi \(x = - a\)
Cho elip (E): \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) với tiêu điểm \({F_2}\left( {\sqrt 5 ;0} \right)\). Tìm tọa độ \(M \in \left( E \right)\) sao cho độ dài \({F_2}M\) nhỏ nhất
Phương pháp giải:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
+ Độ dài bán kính qua tiêu của điểm \(M(x,y)\) trên (E) là: \(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x.\)
\(M{F_1}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = - a\) và có giá trị lớn nhất là \(a + c\) khi \(x = a\)
\(M{F_2}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = a\) và có giá trị lớn nhất là \(a + c\) khi \(x = - a\)
Lời giải chi tiết:
Elip (E): \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) có \(a = 3,b = 2 \Rightarrow c = \sqrt {{a^2} - {b^2}} = \sqrt 5 \)
Độ dài bán kính qua tiêu \(M{F_2} = a - \frac{c}{a}x = 3 - \frac{{\sqrt 5 }}{3}x.\)
Vì \(M{F_2}\) có độ dài nhỏ nhất là \(a - c\) khi \(x = a\) nên
\(M{F_2}\) có độ dài nhỏ nhất là \(3 - \sqrt 5 \) khi \(x = 3.\)
Mà \(M \in (E)\) \( \Rightarrow \frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1 \Rightarrow {y^2} = 4\left( {1 - \frac{{{x^2}}}{9}} \right) = 4\left( {1 - \frac{{{3^2}}}{9}} \right) = 0\)
Vậy \(M\left( {3;0} \right)\) thì \(M{F_2}\) có độ dài nhỏ nhất bằng \(3 - \sqrt 5 \).
Giả sử đường elip (E) là tập hợp các điểm M trong mặt phẳng sao cho \(M{F_1} + M{F_2} = 2a\), ở đó \({F_1}{F_2} = 2c\) với \(0 < c < a\). Ta chọn hệ trục tọa độ \(Oxy\) có gốc là trung điểm của đoạn thẳng \({F_1}{F_2}\). Trục \(Oy\) là đường trung trực của \({F_1}{F_2}\) và \({F_2}\) nằm trên tia \(Ox\) (Hình 8). Khi đó \({F_1}( - c;0),{F_2}(c;0)\) là các tiêu diểm của elip (E)
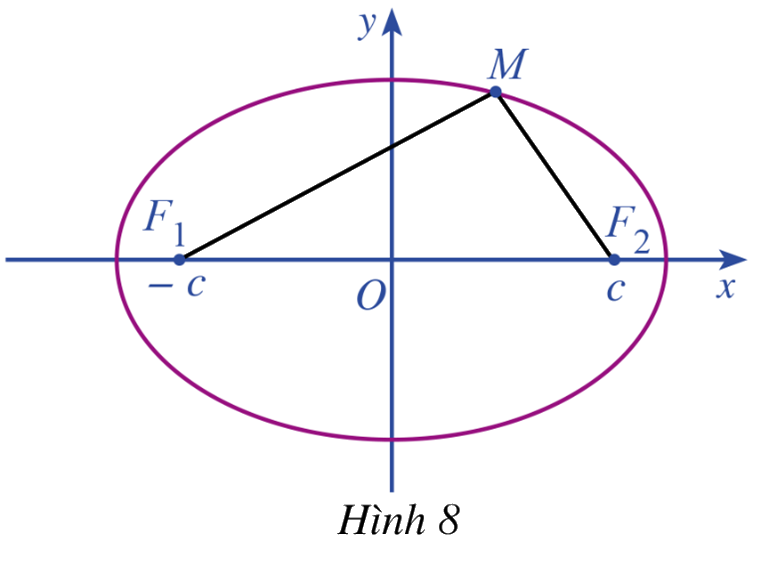
Giả sử điểm \(M\left( {x;y} \right)\) thuộc elip (E)
Chứng minh rằng:
a) \(M{F_1}^2 = {x^2} + 2cx + {c^2} + {y^2}\)
b) \(M{F_2}^2 = {x^2} - 2cx + {c^2} + {y^2}\)
c) \(M{F_1}^2 - M{F_2}^2 = 4cx\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {M{F_1}} = \left( { - c - x; - y} \right) \Rightarrow M{F_1}^2 = {\left( { - c - x} \right)^2} + {y^2} = {x^2} + 2cx + {c^2} + {y^2}\)
b) Ta có: \(\overrightarrow {M{F_2}} = \left( {c - x; - y} \right) \Rightarrow M{F_2}^2 = {\left( {c - x} \right)^2} + {y^2} = {x^2} - 2cx + {c^2} + {y^2}\)
c) \(M{F_1}^2 - M{F_2}^2 = \left( {{x^2} + 2cx + {c^2} + {y^2}} \right) - \left( {{x^2} - 2cx + {c^2} + {y^2}} \right) = 4cx\)
Sử dụng đẳng thức c) ở trên và đẳng thức \(M{F_1} + M{F_2} = 2a\), chứng minh:
a) \(M{F_1} - M{F_2} = \frac{{2c}}{a}x\)
b) \(M{F_1} = a + \frac{c}{a}x\)
c) \(M{F_2} = a - \frac{c}{a}x\)
Lời giải chi tiết:
a) Ta có: \(M{F_1}^2 - M{F_2}^2 = \left( {M{F_1} - M{F_2}} \right)\left( {M{F_1} + M{F_2}} \right) = \left( {M{F_1} - M{F_2}} \right).2a = 4cx\)
\( \Rightarrow M{F_1} - M{F_2} = \frac{{2c}}{a}x\)
b) Ta có: \(\left\{ \begin{array}{l}M{F_1} + M{F_2} = 2a\left( 1 \right)\\M{F_1} - M{F_2} = \frac{{2c}}{a}x\left( 2 \right)\end{array} \right.\)
Cộng hai vế của (1) và (2) ta được: \(2M{F_1} = 2a + \frac{{2c}}{a}x \Rightarrow M{F_1} = a + \frac{c}{a}x\)
c) Ta có: \(M{F_2} = 2a - M{F_1} = 2a - \left( {a + \frac{c}{a}x} \right) = a - \frac{c}{a}x\)
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\). Giả sử M là điểm thuộc elip và có hoành độ là 2. Tìm độ dài của các bán kính qua tiêu của điểm M.
Phương pháp giải:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
+ Độ dài bán kính qua tiêu của điểm \(M(x,y)\) trên (E) là: \(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x.\)
Lời giải chi tiết:
Ta có \(c = \sqrt {{a^2} - {b^2}} = \sqrt {25 - 9} = 4\). Do đó \(e = \frac{c}{a} = \frac{4}{5} = 0,8\). Vậy độ dài các bán kính qua tiêu của điểm M là:
\(M{F_1} = a + \frac{c}{a}x = 5 + 0,8.2 = 6,6;M{F_2} = a - \frac{c}{a}x = 5 - 0,8.2 = 3,4\)
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\). Giả sử \(M\left( {x;y} \right)\) là điểm thuộc elip. Tìm giá trị lớn nhất và bé nhất của bán kính qua tiêu \(M{F_1}\) và \(M{F_2}\)
Phương pháp giải:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
+ Độ dài bán kính qua tiêu của điểm \(M(x,y)\) trên (E) là: \(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x.\)
\(M{F_1}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = - a\) và có giá trị lớn nhất là \(a + c\) khi \(x = a\)
\(M{F_2}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = a\) và có giá trị lớn nhất là \(a + c\) khi \(x = - a\)
Lời giải chi tiết:
Vì \( - a \le x \le a\) nên \(a + \frac{c}{a}\left( { - a} \right) \le a + \frac{c}{a}x \le a + \frac{c}{a}\left( a \right) \Leftrightarrow a - c \le M{F_1} \le a + c\)
Vậy \(M{F_1}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = - a\) và có giá trị lớn nhất là \(a + c\) khi \(x = a\)
Tương tự với \(M{F_2}\), ta có \( - a \le x \le a \Rightarrow a \ge - x \ge - a\) hay \( - a \le x \le a\) nên \(a - \frac{c}{a}\left( a \right) \le a - \frac{c}{a}x \le a - \frac{c}{a}\left( { - a} \right) \Leftrightarrow a - c \le M{F_2} \le a + c\)
Vậy \(M{F_2}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = a\) và có giá trị lớn nhất là \(a + c\) khi \(x = - a\)
Cho elip (E): \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) với tiêu điểm \({F_2}\left( {\sqrt 5 ;0} \right)\). Tìm tọa độ \(M \in \left( E \right)\) sao cho độ dài \({F_2}M\) nhỏ nhất
Phương pháp giải:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
+ Độ dài bán kính qua tiêu của điểm \(M(x,y)\) trên (E) là: \(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x.\)
\(M{F_1}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = - a\) và có giá trị lớn nhất là \(a + c\) khi \(x = a\)
\(M{F_2}\) có giá trị nhỏ nhất là \(a - c\) khi \(x = a\) và có giá trị lớn nhất là \(a + c\) khi \(x = - a\)
Lời giải chi tiết:
Elip (E): \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) có \(a = 3,b = 2 \Rightarrow c = \sqrt {{a^2} - {b^2}} = \sqrt 5 \)
Độ dài bán kính qua tiêu \(M{F_2} = a - \frac{c}{a}x = 3 - \frac{{\sqrt 5 }}{3}x.\)
Vì \(M{F_2}\) có độ dài nhỏ nhất là \(a - c\) khi \(x = a\) nên
\(M{F_2}\) có độ dài nhỏ nhất là \(3 - \sqrt 5 \) khi \(x = 3.\)
Mà \(M \in (E)\) \( \Rightarrow \frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1 \Rightarrow {y^2} = 4\left( {1 - \frac{{{x^2}}}{9}} \right) = 4\left( {1 - \frac{{{3^2}}}{9}} \right) = 0\)
Vậy \(M\left( {3;0} \right)\) thì \(M{F_2}\) có độ dài nhỏ nhất bằng \(3 - \sqrt 5 \).
Giả sử đường elip (E) là tập hợp các điểm M trong mặt phẳng sao cho \(M{F_1} + M{F_2} = 2a\), ở đó \({F_1}{F_2} = 2c\) với \(0 < c < a\). Ta chọn hệ trục tọa độ \(Oxy\) có gốc là trung điểm của đoạn thẳng \({F_1}{F_2}\). Trục \(Oy\) là đường trung trực của \({F_1}{F_2}\) và \({F_2}\) nằm trên tia \(Ox\) (Hình 8). Khi đó \({F_1}( - c;0),{F_2}(c;0)\) là các tiêu diểm của elip (E)
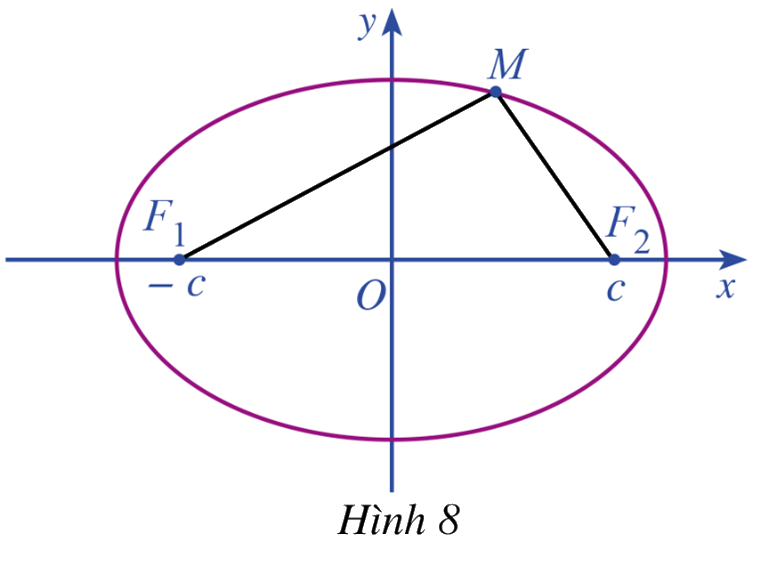
Giả sử điểm \(M\left( {x;y} \right)\) thuộc elip (E)
Chứng minh rằng:
a) \(M{F_1}^2 = {x^2} + 2cx + {c^2} + {y^2}\)
b) \(M{F_2}^2 = {x^2} - 2cx + {c^2} + {y^2}\)
c) \(M{F_1}^2 - M{F_2}^2 = 4cx\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {M{F_1}} = \left( { - c - x; - y} \right) \Rightarrow M{F_1}^2 = {\left( { - c - x} \right)^2} + {y^2} = {x^2} + 2cx + {c^2} + {y^2}\)
b) Ta có: \(\overrightarrow {M{F_2}} = \left( {c - x; - y} \right) \Rightarrow M{F_2}^2 = {\left( {c - x} \right)^2} + {y^2} = {x^2} - 2cx + {c^2} + {y^2}\)
c) \(M{F_1}^2 - M{F_2}^2 = \left( {{x^2} + 2cx + {c^2} + {y^2}} \right) - \left( {{x^2} - 2cx + {c^2} + {y^2}} \right) = 4cx\)
Mục 4 của Chuyên đề học tập Toán 10 - Cánh diều tập trung vào các kiến thức về vectơ, bao gồm các khái niệm cơ bản, các phép toán trên vectơ, và ứng dụng của vectơ trong hình học. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên.
Trang 43 tập trung vào các bài tập vận dụng kiến thức về khái niệm vectơ và các phép toán cơ bản. Các bài tập thường yêu cầu học sinh:
Ví dụ, bài tập 1 yêu cầu xác định vectơ AB từ hai điểm A và B. Để giải bài tập này, học sinh cần hiểu rõ định nghĩa vectơ và cách xác định các yếu tố của vectơ.
Trang 44 tiếp tục củng cố kiến thức về vectơ thông qua các bài tập phức tạp hơn. Các bài tập thường yêu cầu học sinh:
Ví dụ, bài tập 2 yêu cầu chứng minh đẳng thức vectơ AB + BC = AC. Để giải bài tập này, học sinh cần hiểu rõ quy tắc cộng vectơ và áp dụng vào hình học.
Trang 45 là phần bài tập tổng hợp, yêu cầu học sinh vận dụng tất cả các kiến thức đã học về vectơ để giải quyết các bài toán đa dạng. Các bài tập thường yêu cầu học sinh:
Ví dụ, bài tập 3 yêu cầu tìm tọa độ của một điểm khi biết tọa độ của các điểm khác và mối quan hệ giữa chúng thông qua vectơ. Để giải bài tập này, học sinh cần hiểu rõ mối liên hệ giữa vectơ và tọa độ.
Để giải tốt các bài tập về vectơ, học sinh cần:
Học toán không chỉ là việc học thuộc công thức mà còn là việc hiểu bản chất của vấn đề. Hãy dành thời gian suy nghĩ về các khái niệm và tính chất của vectơ, và cố gắng áp dụng chúng vào giải quyết các bài toán. Đừng ngại hỏi thầy cô hoặc bạn bè khi gặp khó khăn. Chúc các em học tốt!
| Bài tập | Nội dung chính | Phương pháp giải |
|---|---|---|
| Trang 43 - Bài 1 | Xác định vectơ | Áp dụng định nghĩa vectơ |
| Trang 44 - Bài 2 | Chứng minh đẳng thức vectơ | Sử dụng quy tắc cộng vectơ |
| Trang 45 - Bài 3 | Tìm tọa độ điểm | Liên hệ vectơ và tọa độ |