Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải quyết các bài tập trong mục 3 trang 58 của Chuyên đề học tập Toán 10 - Cánh diều.
Chúng tôi cam kết cung cấp nội dung chính xác, đầy đủ và giúp bạn nắm vững kiến thức Toán học một cách hiệu quả.
Vẽ parabol (P): \({y^2} = 4x\)
Vẽ parabol (P): \({y^2} = 4x\)
Lời giải chi tiết:
Để vẽ parabol (P): \({y^2} = 4x\) ta có thể làm như sau:
Bước 1: Lập bảng giá trị
x | 0 | 0,25 | 0,25 | 1 | 1 | 2,25 | 2,25 |
y | 0 | -1 | 1 | 2 | -2 | -3 | 3 |
Chú ý rằng tương ứng với mỗi giá trị dương của x có hai giá trị của y đối nhau
Bước 2: Vẽ các điểm cụ thể mà hoành độ và tung độ được xác định như trong bảng giá trị
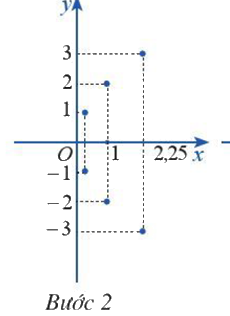
Bước 3: Vẽ đường parabol bên phải trục Oy, đỉnh O, trục đối xứng là Ox, parabol đi qua các điểm được vẽ ở Bước 2
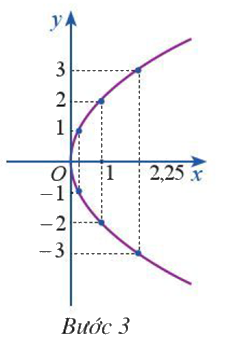
Vẽ parabol (P): \({y^2} = 4x\)
Lời giải chi tiết:
Để vẽ parabol (P): \({y^2} = 4x\) ta có thể làm như sau:
Bước 1: Lập bảng giá trị
x | 0 | 0,25 | 0,25 | 1 | 1 | 2,25 | 2,25 |
y | 0 | -1 | 1 | 2 | -2 | -3 | 3 |
Chú ý rằng tương ứng với mỗi giá trị dương của x có hai giá trị của y đối nhau
Bước 2: Vẽ các điểm cụ thể mà hoành độ và tung độ được xác định như trong bảng giá trị
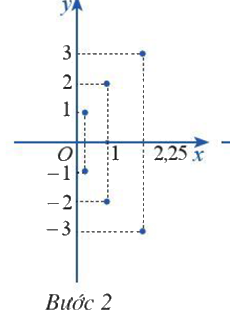
Bước 3: Vẽ đường parabol bên phải trục Oy, đỉnh O, trục đối xứng là Ox, parabol đi qua các điểm được vẽ ở Bước 2
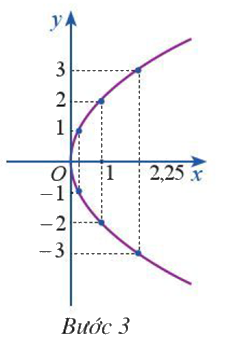
Vẽ parabol \({y^2} = 2px\) biết tiêu điểm của parabol là \(F\left( {\frac{1}{4};0} \right)\)
Phương pháp giải:
Cho parabol có PTCT: \({y^2} = 2px\) trong đó \(p > 0\)
+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)
Lời giải chi tiết:
Ta có tiêu điểm của parabol là \(F\left( {\frac{1}{4};0} \right)\) nên \(\frac{p}{2} = \frac{1}{4} \Rightarrow p = \frac{1}{2} \Rightarrow {y^2} = x\)
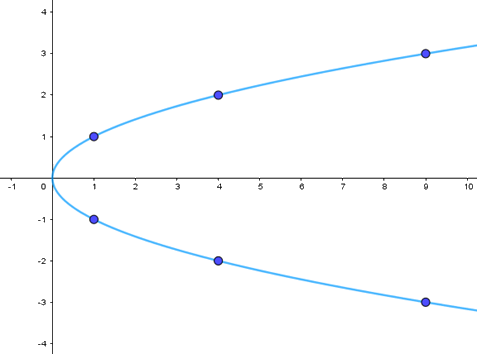
Để vẽ parabol (P): \({y^2} = x\) ta có thể làm như sau:
Bước 1: Lập bảng giá trị
x | 0 | 1 | 1 | 4 | 4 | 9 | 9 |
y | 0 | -1 | 1 | 2 | -2 | -3 | 3 |
Chú ý rằng tương ứng với mỗi giá trị dương của x có hai giá trị của y đối nhau
Bước 2: Vẽ các điểm cụ thể mà hoành độ và tung độ được xác định như trong bảng giá trị
Bước 3: Vẽ đường parabol bên phải trục Oy, đỉnh O, trục đối xứng là Ox, parabol đi qua các điểm được vẽ ở Bước 2
Vẽ parabol \({y^2} = 2px\) biết tiêu điểm của parabol là \(F\left( {\frac{1}{4};0} \right)\)
Phương pháp giải:
Cho parabol có PTCT: \({y^2} = 2px\) trong đó \(p > 0\)
+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)
Lời giải chi tiết:
Ta có tiêu điểm của parabol là \(F\left( {\frac{1}{4};0} \right)\) nên \(\frac{p}{2} = \frac{1}{4} \Rightarrow p = \frac{1}{2} \Rightarrow {y^2} = x\)
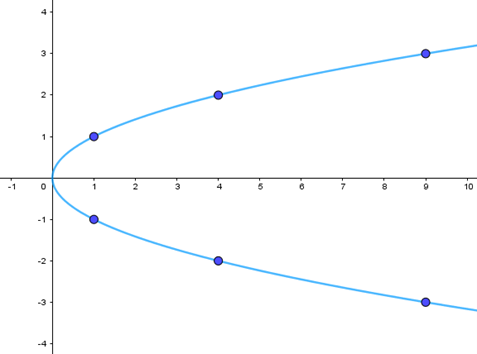
Để vẽ parabol (P): \({y^2} = x\) ta có thể làm như sau:
Bước 1: Lập bảng giá trị
x | 0 | 1 | 1 | 4 | 4 | 9 | 9 |
y | 0 | -1 | 1 | 2 | -2 | -3 | 3 |
Chú ý rằng tương ứng với mỗi giá trị dương của x có hai giá trị của y đối nhau
Bước 2: Vẽ các điểm cụ thể mà hoành độ và tung độ được xác định như trong bảng giá trị
Bước 3: Vẽ đường parabol bên phải trục Oy, đỉnh O, trục đối xứng là Ox, parabol đi qua các điểm được vẽ ở Bước 2
Mục 3 trang 58 trong Chuyên đề học tập Toán 10 - Cánh diều thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững kiến thức lý thuyết liên quan, hiểu rõ các định nghĩa, định lý và công thức đã học. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập, kèm theo các giải thích rõ ràng để giúp bạn hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Để đảm bảo tính chính xác và dễ hiểu, chúng ta sẽ đi qua từng bài tập trong mục 3 trang 58. Mỗi bài tập sẽ được trình bày theo cấu trúc sau:
Đề bài: Cho hàm số y = x2 - 4x + 3. Tìm tọa độ đỉnh của parabol.
Phân tích đề bài: Bài toán yêu cầu tìm tọa độ đỉnh của parabol. Để làm được điều này, ta cần sử dụng công thức tính tọa độ đỉnh của parabol y = ax2 + bx + c.
Lời giải:
Kết luận: Tọa độ đỉnh của parabol là (2; -1).
Đề bài: Giải phương trình: x2 - 5x + 6 = 0.
Phân tích đề bài: Bài toán yêu cầu giải phương trình bậc hai. Ta có thể sử dụng phương pháp phân tích thành nhân tử hoặc sử dụng công thức nghiệm của phương trình bậc hai.
Lời giải:
Kết luận: Phương trình có hai nghiệm là x = 2 và x = 3.
Đề bài: Tìm tập xác định của hàm số y = √(x - 1).
Phân tích đề bài: Bài toán yêu cầu tìm tập xác định của hàm số. Để hàm số có nghĩa, biểu thức dưới dấu căn phải lớn hơn hoặc bằng 0.
Lời giải:
Kết luận: Tập xác định của hàm số là [1; +∞).
Khi giải các bài tập Toán 10, đặc biệt là trong Chuyên đề học tập, bạn cần lưu ý những điều sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 58 của Chuyên đề học tập Toán 10 - Cánh diều. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!