Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 1 trang 49 Chuyên đề học tập Toán 10 - Cánh diều. Bài viết này cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 10, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Trong mặt phẳng tọa độ \(Oxy\), ta xét hypebol (H) với phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\) (Hình 13)
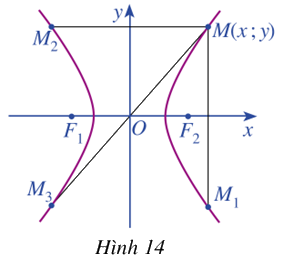
Trong mặt phẳng tọa độ \(Oxy\), ta xét hypebol (H) với phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\) (Hình 14). Cho điểm \(M\left( {x;y} \right)\) nằm trên hypebol (H). Gọi \({M_1},{M_2},{M_3}\) lần lượt là điểm đối xứng của M qua trục Ox, trục Oy và gốc O. Các điểm \({M_1},{M_2},{M_3}\) có nằm trên hypebol (H) không? Tại sao?
Lời giải chi tiết:
+ Điểm \({M_1}\left( {x; - y} \right)\) thuộc hypebol (H) vì \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{{( - y)}^2}}}{{{b^2}}} = 1\)
+ Điểm \({M_2}\left( { - x;y} \right)\) thuộc hypebol (H) vì \(\frac{{{{( - x)}^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
+ Điểm \({M_3}\left( { - x; - y} \right)\) thuộc hypebol (H) vì \(\frac{{{{( - x)}^2}}}{{{a^2}}} - \frac{{{{( - y)}^2}}}{{{b^2}}} = 1\)
Trong mặt phẳng tọa độ \(Oxy\), ta xét hypebol (H) với phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\) (Hình 13)
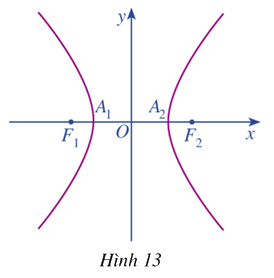
a) Tìm tọa độ của hai tiêu điểm \({F_1},{F_2}\) của hypebol \(\left( H \right)\)
b) Hypebol \(\left( H \right)\) cắt trục \(Ox\) tại các điểm \({A_1},{A_2}\). Tìm độ dài các đoạn thẳng \(O{A_1},O{A_2}\)
Phương pháp giải:
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\). Khi đó ta có:
+ Tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\)
+ Độ dài trục thực: \(2a\), độ dài trục ảo: \(2b\)
Lời giải chi tiết:
a) \({F_1},{F_2}\) là tiêu điểm của hypebol (H) có tọa độ \({F_1}( - c;0),{F_2}(c;0)\) với \(c = \sqrt {{a^2} + {b^2}} \)
b) \({A_1},{A_2}\) là giao điểm của (H) với Ox \( \Rightarrow {y_{{A_1}}} = {y_{{A_2}}} = 0 \Rightarrow \frac{{{x_{{A_1}}}^2}}{{{a^2}}} = 1;\frac{{{x_{{A_2}}}^2}}{{{a^2}}} = 1 \Rightarrow {x_{{A_1}}} = - a;{x_{{A_2}}} = a\)
Hay \({A_1}( - a;0),{A_2}(a;0)\) \( \Rightarrow O{A_1} = O{A_2} = a\)
Trong mặt phẳng tọa độ \(Oxy\), ta xét hypebol (H) với phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\) (Hình 13)
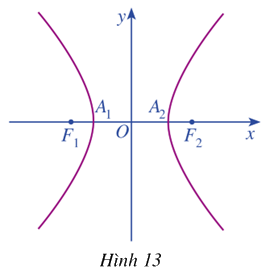
a) Tìm tọa độ của hai tiêu điểm \({F_1},{F_2}\) của hypebol \(\left( H \right)\)
b) Hypebol \(\left( H \right)\) cắt trục \(Ox\) tại các điểm \({A_1},{A_2}\). Tìm độ dài các đoạn thẳng \(O{A_1},O{A_2}\)
Phương pháp giải:
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\). Khi đó ta có:
+ Tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\)
+ Độ dài trục thực: \(2a\), độ dài trục ảo: \(2b\)
Lời giải chi tiết:
a) \({F_1},{F_2}\) là tiêu điểm của hypebol (H) có tọa độ \({F_1}( - c;0),{F_2}(c;0)\) với \(c = \sqrt {{a^2} + {b^2}} \)
b) \({A_1},{A_2}\) là giao điểm của (H) với Ox \( \Rightarrow {y_{{A_1}}} = {y_{{A_2}}} = 0 \Rightarrow \frac{{{x_{{A_1}}}^2}}{{{a^2}}} = 1;\frac{{{x_{{A_2}}}^2}}{{{a^2}}} = 1 \Rightarrow {x_{{A_1}}} = - a;{x_{{A_2}}} = a\)
Hay \({A_1}( - a;0),{A_2}(a;0)\) \( \Rightarrow O{A_1} = O{A_2} = a\)
Trong mặt phẳng tọa độ \(Oxy\), ta xét hypebol (H) với phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\) (Hình 14). Cho điểm \(M\left( {x;y} \right)\) nằm trên hypebol (H). Gọi \({M_1},{M_2},{M_3}\) lần lượt là điểm đối xứng của M qua trục Ox, trục Oy và gốc O. Các điểm \({M_1},{M_2},{M_3}\) có nằm trên hypebol (H) không? Tại sao?
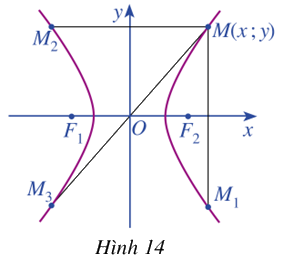
Lời giải chi tiết:
+ Điểm \({M_1}\left( {x; - y} \right)\) thuộc hypebol (H) vì \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{{( - y)}^2}}}{{{b^2}}} = 1\)
+ Điểm \({M_2}\left( { - x;y} \right)\) thuộc hypebol (H) vì \(\frac{{{{( - x)}^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
+ Điểm \({M_3}\left( { - x; - y} \right)\) thuộc hypebol (H) vì \(\frac{{{{( - x)}^2}}}{{{a^2}}} - \frac{{{{( - y)}^2}}}{{{b^2}}} = 1\)
Mục 1 trang 49 trong Chuyên đề học tập Toán 10 - Cánh diều thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững kiến thức nền tảng, hiểu rõ các định nghĩa, định lý và công thức liên quan. Bài viết này sẽ cung cấp một hướng dẫn chi tiết về cách tiếp cận và giải quyết các bài tập trong mục này.
Thông thường, Mục 1 trang 49 sẽ xoay quanh các chủ đề như:
Dưới đây là giải chi tiết các bài tập thường gặp trong Mục 1 trang 49 Chuyên đề học tập Toán 10 - Cánh diều. Lưu ý rằng, các bài tập cụ thể có thể khác nhau tùy thuộc vào từng phiên bản sách.
Để tính độ dài của vectơ a = (x; y; z), ta sử dụng công thức: |a| = √(x² + y² + z²). Ví dụ, nếu a = (1; 2; 3), thì |a| = √(1² + 2² + 3²) = √14.
Phương trình đường thẳng đi qua điểm M(x₀; y₀; z₀) và có vectơ chỉ phương u = (a; b; c) được cho bởi:
x = x₀ + at
y = y₀ + bt
z = z₀ + ct
Tích vô hướng của hai vectơ a = (x₁; y₁; z₁) và b = (x₂; y₂; z₂) được tính bằng công thức: a ⋅ b = x₁x₂ + y₁y₂ + z₁z₂. Nếu a ⋅ b = 0, thì hai vectơ vuông góc với nhau.
Để giải các bài tập trong Mục 1 trang 49 một cách nhanh chóng và hiệu quả, bạn có thể áp dụng một số mẹo sau:
Kiến thức về vectơ, hình học tọa độ, đạo hàm và tích phân có ứng dụng rất lớn trong thực tế, đặc biệt trong các lĩnh vực như:
Hy vọng rằng, với hướng dẫn chi tiết và các mẹo giải nhanh được cung cấp trong bài viết này, bạn sẽ tự tin giải quyết các bài tập trong Mục 1 trang 49 Chuyên đề học tập Toán 10 - Cánh diều. Chúc bạn học tập tốt!