Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục 4 trang 53 của Chuyên đề học tập Toán 10 - Cánh diều.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Trong mặt phẳng, xét đường hypebol (H) là tập hợp các điểm M sao cho \(\left| {M{F_1} - M{F_2}} \right| = 2a\), ở đó \({F_1}{F_2} = 2c\) với \(c > a > 0\).
Với mỗi điểm M thuộc hypebol (H), từ hai đẳng thức \(M{F_1}^2 - M{F_2}^2 = 4cx\) và \(\left| {M{F_1} - M{F_2}} \right| = 2a\), chứng minh \(M{F_1} = \left| {a + \frac{c}{a}x} \right| = \left| {a + ex} \right|\) và \(M{F_2} = \left| {a - \frac{c}{a}x} \right| = \left| {a - ex} \right|\)
Lời giải chi tiết:
+ Ta có: \(M{F_1}^2 - M{F_2}^2 = \left( {M{F_1} - M{F_2}} \right)\left( {M{F_1} + M{F_2}} \right) = \left( {M{F_1} - M{F_2}} \right).\left| {2a} \right| = 4cx\)
\( \Rightarrow M{F_1} - M{F_2} = \frac{{2c}}{{\left| a \right|}}x\)
+ Ta có: \(\left\{ \begin{array}{l}M{F_1} + M{F_2} = \left| {2a} \right|\quad \left( 1 \right)\\M{F_1} - M{F_2} = \frac{{2c}}{{\left| a \right|}}x\quad \left( 2 \right)\end{array} \right.\)
Từ (1) và (2) suy ra:
\(2M{F_1} = \left| {2a} \right| + \frac{{2c}}{{\left| a \right|}}x \Rightarrow M{F_1} = \left| a \right| + \frac{c}{{\left| a \right|}}x = \left| {a + \frac{c}{a}x} \right| = \left| {a + ex} \right|\)
\(M{F_2} = 2\left| a \right| - M{F_1} = 2\left| a \right| - \left( {\left| a \right| + \frac{c}{{\left| a \right|}}x} \right) = \left| a \right| - \frac{c}{{\left| a \right|}}x\)\( = \left| {a - \frac{c}{a}x} \right| = \left| {a - ex} \right|\)
Cho hypebol (H) có phương trình chính tắc: \(\frac{{{x^2}}}{{144}} - \frac{{{y^2}}}{{25}} = 1\). Giả sử điểm M là diderm chuẩn thuộc hypebol có hoành độ là 15. Tìm độ dài các bán kính qua tiêu của điểm M.
Phương pháp giải:
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\). Khi đó ta có:
+ Độ dài hai bán kính qua tiêu của điểm \(M(x;y)\) là: \(M{F_1} = \left| {a + \frac{c}{a}x} \right|;M{F_2} = \left| {a - \frac{c}{a}x} \right|\)
Lời giải chi tiết:
Ta có \(a = 12,b = 3,c = \sqrt {{a^2} + {b^2}} = \sqrt {144 + 9} = 3\sqrt {17} \).
Do đó \(e = \frac{{3\sqrt {17} }}{{12}} = \frac{{\sqrt {17} }}{4}\).
Vậy độ dài các bán kính qua tiêu của điểm M là:
\(M{F_1} = \left| {12 + \frac{{\sqrt {17} }}{4}.15} \right|;M{F_2} = \left| {12 - \frac{{\sqrt {17} }}{4}.15} \right|\)
Trong mặt phẳng, xét đường hypebol (H) là tập hợp các điểm M sao cho \(\left| {M{F_1} - M{F_2}} \right| = 2a\), ở đó \({F_1}{F_2} = 2c\) với \(c > a > 0\). Ta chọn hệ trục tọa độ \(Oxy\) có gốc là trung điểm của đoạn thẳng \({F_1}{F_2}\). Trục \(Oy\) là đường trung trực của \({F_1}{F_2}\) và \({F_2}\) nằm trên tia \(Ox\) (Hình 16). Khi đó \({F_1}( - c;0),{F_2}(c;0)\) là các tiêu diểm của hypebol (H)
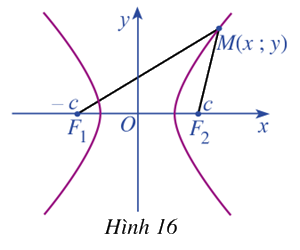
Giả sử điểm \(M\left( {x;y} \right)\) thuộc hypebol (H), chứng minh:
a) \(M{F_1}^2 = {x^2} + 2cx + {c^2} + {y^2}\)
b) \(M{F_2}^2 = {x^2} - 2cx + {c^2} + {y^2}\)
c) \(M{F_1}^2 - M{F_2}^2 = 4cx\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {M{F_1}} = \left( { - c - x; - y} \right) \Rightarrow M{F_1}^2 = {\left( { - c - x} \right)^2} + {y^2} = {x^2} + 2cx + {c^2} + {y^2}\)
b) Ta có: \(\overrightarrow {M{F_2}} = \left( {c - x; - y} \right) \Rightarrow M{F_2}^2 = {\left( {c - x} \right)^2} + {y^2} = {x^2} - 2cx + {c^2} + {y^2}\)
c) \(M{F_1}^2 - M{F_2}^2 = \left( {{x^2} + 2cx + {c^2} + {y^2}} \right) - \left( {{x^2} - 2cx + {c^2} + {y^2}} \right) = 4cx\)
Trong mặt phẳng, xét đường hypebol (H) là tập hợp các điểm M sao cho \(\left| {M{F_1} - M{F_2}} \right| = 2a\), ở đó \({F_1}{F_2} = 2c\) với \(c > a > 0\). Ta chọn hệ trục tọa độ \(Oxy\) có gốc là trung điểm của đoạn thẳng \({F_1}{F_2}\). Trục \(Oy\) là đường trung trực của \({F_1}{F_2}\) và \({F_2}\) nằm trên tia \(Ox\) (Hình 16). Khi đó \({F_1}( - c;0),{F_2}(c;0)\) là các tiêu diểm của hypebol (H)
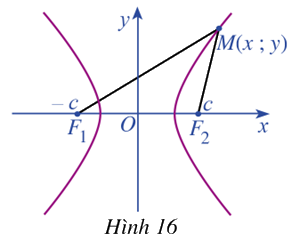
Giả sử điểm \(M\left( {x;y} \right)\) thuộc hypebol (H), chứng minh:
a) \(M{F_1}^2 = {x^2} + 2cx + {c^2} + {y^2}\)
b) \(M{F_2}^2 = {x^2} - 2cx + {c^2} + {y^2}\)
c) \(M{F_1}^2 - M{F_2}^2 = 4cx\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {M{F_1}} = \left( { - c - x; - y} \right) \Rightarrow M{F_1}^2 = {\left( { - c - x} \right)^2} + {y^2} = {x^2} + 2cx + {c^2} + {y^2}\)
b) Ta có: \(\overrightarrow {M{F_2}} = \left( {c - x; - y} \right) \Rightarrow M{F_2}^2 = {\left( {c - x} \right)^2} + {y^2} = {x^2} - 2cx + {c^2} + {y^2}\)
c) \(M{F_1}^2 - M{F_2}^2 = \left( {{x^2} + 2cx + {c^2} + {y^2}} \right) - \left( {{x^2} - 2cx + {c^2} + {y^2}} \right) = 4cx\)
Với mỗi điểm M thuộc hypebol (H), từ hai đẳng thức \(M{F_1}^2 - M{F_2}^2 = 4cx\) và \(\left| {M{F_1} - M{F_2}} \right| = 2a\), chứng minh \(M{F_1} = \left| {a + \frac{c}{a}x} \right| = \left| {a + ex} \right|\) và \(M{F_2} = \left| {a - \frac{c}{a}x} \right| = \left| {a - ex} \right|\)
Lời giải chi tiết:
+ Ta có: \(M{F_1}^2 - M{F_2}^2 = \left( {M{F_1} - M{F_2}} \right)\left( {M{F_1} + M{F_2}} \right) = \left( {M{F_1} - M{F_2}} \right).\left| {2a} \right| = 4cx\)
\( \Rightarrow M{F_1} - M{F_2} = \frac{{2c}}{{\left| a \right|}}x\)
+ Ta có: \(\left\{ \begin{array}{l}M{F_1} + M{F_2} = \left| {2a} \right|\quad \left( 1 \right)\\M{F_1} - M{F_2} = \frac{{2c}}{{\left| a \right|}}x\quad \left( 2 \right)\end{array} \right.\)
Từ (1) và (2) suy ra:
\(2M{F_1} = \left| {2a} \right| + \frac{{2c}}{{\left| a \right|}}x \Rightarrow M{F_1} = \left| a \right| + \frac{c}{{\left| a \right|}}x = \left| {a + \frac{c}{a}x} \right| = \left| {a + ex} \right|\)
\(M{F_2} = 2\left| a \right| - M{F_1} = 2\left| a \right| - \left( {\left| a \right| + \frac{c}{{\left| a \right|}}x} \right) = \left| a \right| - \frac{c}{{\left| a \right|}}x\)\( = \left| {a - \frac{c}{a}x} \right| = \left| {a - ex} \right|\)
Cho hypebol (H) có phương trình chính tắc: \(\frac{{{x^2}}}{{144}} - \frac{{{y^2}}}{{25}} = 1\). Giả sử điểm M là diderm chuẩn thuộc hypebol có hoành độ là 15. Tìm độ dài các bán kính qua tiêu của điểm M.
Phương pháp giải:
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\). Khi đó ta có:
+ Độ dài hai bán kính qua tiêu của điểm \(M(x;y)\) là: \(M{F_1} = \left| {a + \frac{c}{a}x} \right|;M{F_2} = \left| {a - \frac{c}{a}x} \right|\)
Lời giải chi tiết:
Ta có \(a = 12,b = 3,c = \sqrt {{a^2} + {b^2}} = \sqrt {144 + 9} = 3\sqrt {17} \).
Do đó \(e = \frac{{3\sqrt {17} }}{{12}} = \frac{{\sqrt {17} }}{4}\).
Vậy độ dài các bán kính qua tiêu của điểm M là:
\(M{F_1} = \left| {12 + \frac{{\sqrt {17} }}{4}.15} \right|;M{F_2} = \left| {12 - \frac{{\sqrt {17} }}{4}.15} \right|\)
Mục 4 trang 53 Chuyên đề học tập Toán 10 - Cánh diều tập trung vào việc vận dụng các kiến thức về vectơ trong không gian để giải quyết các bài toán hình học. Các bài tập thường yêu cầu học sinh xác định mối quan hệ giữa các vectơ, tính toán độ dài vectơ, tích vô hướng và ứng dụng vào việc chứng minh các tính chất hình học.
Để giúp các em học sinh hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 4 trang 53, chúng ta sẽ đi vào phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh xác định các vectơ trong một hình cho trước. Để giải bài tập này, học sinh cần nắm vững định nghĩa của vectơ, cách biểu diễn vectơ và các quy tắc cộng, trừ vectơ.
Bài tập này yêu cầu học sinh tính độ dài của một vectơ. Để giải bài tập này, học sinh cần nắm vững công thức tính độ dài vectơ và áp dụng công thức một cách chính xác.
Công thức tính độ dài vectơ a = (x; y; z) là: |a| = √(x² + y² + z²)
Bài tập này yêu cầu học sinh tính tích vô hướng của hai vectơ. Để giải bài tập này, học sinh cần nắm vững định nghĩa của tích vô hướng và công thức tính tích vô hướng.
Công thức tính tích vô hướng của hai vectơ a = (x1; y1; z1) và b = (x2; y2; z2) là: a.b = x1x2 + y1y2 + z1z2
Bài tập này yêu cầu học sinh sử dụng tích vô hướng để chứng minh hai vectơ vuông góc. Để giải bài tập này, học sinh cần nắm vững tính chất của tích vô hướng: hai vectơ vuông góc khi và chỉ khi tích vô hướng của chúng bằng 0.
Để giải các bài toán liên quan đến vectơ trong không gian một cách hiệu quả, học sinh cần:
Ví dụ: Cho hai vectơ a = (1; 2; 3) và b = (-2; 1; 0). Tính tích vô hướng của hai vectơ này.
Giải: Tích vô hướng của hai vectơ a và b là:
a.b = (1)(-2) + (2)(1) + (3)(0) = -2 + 2 + 0 = 0
Vậy, tích vô hướng của hai vectơ a và b bằng 0, suy ra hai vectơ này vuông góc với nhau.
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, các em học sinh có thể tự giải thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tham khảo các bài giảng online và các video hướng dẫn giải toán trên giaitoan.edu.vn.
Hy vọng rằng, với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 4 trang 53 Chuyên đề học tập Toán 10 - Cánh diều. Chúc các em học tập tốt!