Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải quyết các bài tập trong mục 2 trang 41 của Chuyên đề học tập Toán 10 - Cánh diều.
Chúng tôi hiểu rằng việc học toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải chính xác, rõ ràng và dễ tiếp thu nhất.
a) Nêu nhận xét về vị trí bốn đỉnh của elip \(\left( E \right)\) với bốn cạnh của hình chữ nhật cơ sở.
a) Nêu nhận xét về vị trí bốn đỉnh của elip \(\left( E \right)\) với bốn cạnh của hình chữ nhật cơ sở.
b) Cho điểm \(M\left( {x;y} \right)\) thuộc elip \(\left( E \right)\). Tìm giá trị nhỏ nhất và lớn nhất của x và của y.
Lời giải chi tiết:
a) Trong mặt phẳng tọa độ \(Oxy\), ta xét Elip \(\left( E \right)\) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\) . Khi đó ta có:
+ Hình chữ nhật cơ sở có bốn đỉnh là \(P\left( { - a;b} \right),Q\left( {a;b} \right),R\left( {a; - b} \right),S\left( { - a; - b} \right)\)
+ Bốn đỉnh của elip là trung điểm của các cạnh của hình chữ nhật cơ sở
b) Nếu điểm \(M\left( {x;y} \right)\) thuộc elip \(\left( E \right)\) thì \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
\( \Rightarrow \frac{{{x^2}}}{{{a^2}}} \le 1,\frac{{{y^2}}}{{{b^2}}} \le 1 \Leftrightarrow {x^2} \le {a^2},{y^2} \le {b^2}\)
\( \Leftrightarrow - a \le x \le a, - b \le y \le b\).
Dó đó mọi điểm của elip nếu không phải đỉnh thì đều nằm trong hình chữ nhật
Khi đó Giá trị lớn nhất và nhỏ nhất của x là a và -a, Giá trị lớn nhất và nhỏ nhất của y là b và -b
Viết phương trình chính tắc của elip, biết \({A_1}\left( { - 4;0} \right),{B_2}\left( {0;2} \right)\) là hai đỉnh của nó
Phương pháp giải:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\) . Khi đó ta có 4 đỉnh là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right).\)
Lời giải chi tiết:
Ta có \({A_1}\left( { - 4;0} \right),{B_2}\left( {0;2} \right)\) là hai đỉnh của elip, suy ra \(a = 4,b = 2\).
Khi đó phương trình chính tắc của elip là \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{4} = 1\)
a) Nêu nhận xét về vị trí bốn đỉnh của elip \(\left( E \right)\) với bốn cạnh của hình chữ nhật cơ sở.
b) Cho điểm \(M\left( {x;y} \right)\) thuộc elip \(\left( E \right)\). Tìm giá trị nhỏ nhất và lớn nhất của x và của y.
Lời giải chi tiết:
a) Trong mặt phẳng tọa độ \(Oxy\), ta xét Elip \(\left( E \right)\) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\) . Khi đó ta có:
+ Hình chữ nhật cơ sở có bốn đỉnh là \(P\left( { - a;b} \right),Q\left( {a;b} \right),R\left( {a; - b} \right),S\left( { - a; - b} \right)\)
+ Bốn đỉnh của elip là trung điểm của các cạnh của hình chữ nhật cơ sở
b) Nếu điểm \(M\left( {x;y} \right)\) thuộc elip \(\left( E \right)\) thì \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
\( \Rightarrow \frac{{{x^2}}}{{{a^2}}} \le 1,\frac{{{y^2}}}{{{b^2}}} \le 1 \Leftrightarrow {x^2} \le {a^2},{y^2} \le {b^2}\)
\( \Leftrightarrow - a \le x \le a, - b \le y \le b\).
Dó đó mọi điểm của elip nếu không phải đỉnh thì đều nằm trong hình chữ nhật
Khi đó Giá trị lớn nhất và nhỏ nhất của x là a và -a, Giá trị lớn nhất và nhỏ nhất của y là b và -b
Viết phương trình chính tắc của elip, biết \({A_1}\left( { - 4;0} \right),{B_2}\left( {0;2} \right)\) là hai đỉnh của nó
Phương pháp giải:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\) . Khi đó ta có 4 đỉnh là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right).\)
Lời giải chi tiết:
Ta có \({A_1}\left( { - 4;0} \right),{B_2}\left( {0;2} \right)\) là hai đỉnh của elip, suy ra \(a = 4,b = 2\).
Khi đó phương trình chính tắc của elip là \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{4} = 1\)
Quan sát elip \(\left( E \right)\) phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > b > 0\) và hình chữ nhật cơ sở PQRS của \(\left( E \right)\)(Hình 5)
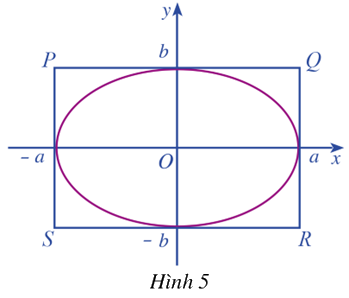
a) Tính tỉ số giữa hai cạnh \(\frac{{QR}}{{PQ}}\) của hình chữ nhật \(PQRS\)
b) Tỉ số \(\frac{{QR}}{{PQ}}\) phản ánh đặc điểm gì của \(\left( E \right)\) về hình dạng?
Phương pháp giải:
Trong mặt phẳng tọa độ \(Oxy\), ta xét Elip \(\left( E \right)\) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\) . Khi đó ta có hình chữ nhật cơ sở có bốn đỉnh là \(P\left( { - a;b} \right),Q\left( {a;b} \right),R\left( {a; - b} \right),S\left( { - a; - b} \right)\)
Lời giải chi tiết:
a) Ta có hình chữ nhật cơ sở có bốn đỉnh là \(P\left( { - a;b} \right),Q\left( {a;b} \right),R\left( {a; - b} \right),S\left( { - a; - b} \right)\)
Suy ra \(QR = 2b,PQ = 2a \Rightarrow \frac{{QR}}{{PQ}} = \frac{{2b}}{{2a}} = \frac{b}{a}\)
b) Ta có \(\frac{{QR}}{{PQ}} = \frac{b}{a}\), vì \(0 < b < a\) nên \(0 < \frac{b}{a} < 1\). Tỉ số \(\frac{b}{a}\) phản ánh cụ thể hình dạng của \(\left( E \right)\) như sau:
+ Nếu tỉ số \(\frac{b}{a}\) càng bé thì hình chữ nhật cơ sở càng “dẹt”, do đó \(\left( E \right)\) càng “gầy”
+ Nếu tỉ số \(\frac{b}{a}\) càng lớn thì b càng gần a và hình chữ nhật cơ sở càng gần với hình vuông, do đó \(\left( E \right)\) càng “béo”
Quan sát elip \(\left( E \right)\) phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > b > 0\) và hình chữ nhật cơ sở PQRS của \(\left( E \right)\)(Hình 5)
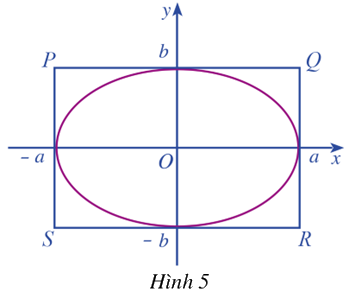
a) Tính tỉ số giữa hai cạnh \(\frac{{QR}}{{PQ}}\) của hình chữ nhật \(PQRS\)
b) Tỉ số \(\frac{{QR}}{{PQ}}\) phản ánh đặc điểm gì của \(\left( E \right)\) về hình dạng?
Phương pháp giải:
Trong mặt phẳng tọa độ \(Oxy\), ta xét Elip \(\left( E \right)\) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\) . Khi đó ta có hình chữ nhật cơ sở có bốn đỉnh là \(P\left( { - a;b} \right),Q\left( {a;b} \right),R\left( {a; - b} \right),S\left( { - a; - b} \right)\)
Lời giải chi tiết:
a) Ta có hình chữ nhật cơ sở có bốn đỉnh là \(P\left( { - a;b} \right),Q\left( {a;b} \right),R\left( {a; - b} \right),S\left( { - a; - b} \right)\)
Suy ra \(QR = 2b,PQ = 2a \Rightarrow \frac{{QR}}{{PQ}} = \frac{{2b}}{{2a}} = \frac{b}{a}\)
b) Ta có \(\frac{{QR}}{{PQ}} = \frac{b}{a}\), vì \(0 < b < a\) nên \(0 < \frac{b}{a} < 1\). Tỉ số \(\frac{b}{a}\) phản ánh cụ thể hình dạng của \(\left( E \right)\) như sau:
+ Nếu tỉ số \(\frac{b}{a}\) càng bé thì hình chữ nhật cơ sở càng “dẹt”, do đó \(\left( E \right)\) càng “gầy”
+ Nếu tỉ số \(\frac{b}{a}\) càng lớn thì b càng gần a và hình chữ nhật cơ sở càng gần với hình vuông, do đó \(\left( E \right)\) càng “béo”
Mục 2 trang 41 Chuyên đề học tập Toán 10 - Cánh diều tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học phẳng. Các bài tập trong mục này thường yêu cầu học sinh phải hiểu rõ các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của chúng. Việc nắm vững các kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Mục 2 bao gồm một loạt các bài tập với độ khó tăng dần. Các bài tập đầu tiên thường tập trung vào việc tính toán các phép toán vectơ cơ bản. Sau đó, các bài tập trở nên phức tạp hơn, yêu cầu học sinh phải kết hợp nhiều kiến thức khác nhau để giải quyết. Dưới đây là phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh thực hiện các phép cộng và trừ vectơ. Để giải bài tập này, học sinh cần nhớ các quy tắc cộng và trừ vectơ: vectơ tổng (hiệu) của hai vectơ có cùng điểm gốc là vectơ có điểm ngút là điểm ngút của vectơ thứ hai (thứ nhất) khi cộng (trừ). Ví dụ, nếu có hai vectơ a và b, thì a + b là vectơ có điểm ngút là điểm ngút của b khi cộng với a.
Bài tập này yêu cầu học sinh áp dụng quy tắc cộng vectơ để tìm vectơ tổng của hai vectơ. Học sinh cần xác định vị trí của các điểm A, B, C, D trên mặt phẳng tọa độ hoặc sử dụng các tính chất hình học để tìm ra vectơ AB và CD, sau đó cộng chúng lại để tìm vectơ AB + CD.
Bài tập này là một bài toán tìm điểm thỏa mãn một điều kiện vectơ. Để giải bài tập này, học sinh có thể sử dụng quy tắc hình bình hành. Theo quy tắc hình bình hành, nếu MA + MB = MC, thì M là đỉnh thứ tư của hình bình hành MACB. Do đó, học sinh cần xác định vị trí của điểm M sao cho MACB là một hình bình hành.
Ví dụ: Cho hai vectơ a = (1; 2) và b = (-3; 1). Tính a + b.
Giải:a + b = (1 + (-3); 2 + 1) = (-2; 3)
Để củng cố kiến thức và kỹ năng giải bài tập vectơ, bạn có thể luyện tập thêm với các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, bạn cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán.
Việc giải các bài tập trong mục 2 trang 41 Chuyên đề học tập Toán 10 - Cánh diều đòi hỏi học sinh phải nắm vững các kiến thức về vectơ và các phép toán vectơ. Bằng cách áp dụng các phương pháp giải bài tập hiệu quả và luyện tập thường xuyên, bạn có thể tự tin giải quyết các bài toán vectơ một cách nhanh chóng và chính xác. Chúc bạn học tốt!