Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 66 Chuyên đề học tập Toán 10 – Cánh diều. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em hiểu rõ kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp các bài giải chuẩn xác, dễ hiểu và nhiều tài liệu học tập hữu ích khác.
Cho hình chữ nhật ABCD với bốn đỉnh \(A\left( { - 4;3} \right),B\left( {4;3} \right),C\left( {4; - 3} \right),D\left( { - 4; - 3} \right).\)
Đề bài
Cho hình chữ nhật ABCD với bốn đỉnh \(A\left( { - 4;3} \right),B\left( {4;3} \right),C\left( {4; - 3} \right),D\left( { - 4; - 3} \right).\)
a) Viết phương trình chính tắc của elip nhận ABCD là hình chữ nhật cơ sở. Vẽ elip đó
b) Viết phương trình chính tắc của hypebol nhận ABCD là hình chữ nhật cơ sở. Vẽ hypebol đó
Phương pháp giải - Xem chi tiết
Trong mặt phẳng tọa độ \(Oxy\), ta xét Elip \(\left( E \right)\) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\) . Khi đó ta có:
+ Hình chữ nhật cơ sở có bốn đỉnh là \(P\left( { - a;b} \right),Q\left( {a;b} \right),R\left( {a; - b} \right),S\left( { - a; - b} \right)\)
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\). Khi đó ta có:
+ Hình chữ nhật cơ sở có 4 đỉnh \(P\left( { - a;b} \right),Q\left( {a;b} \right),R\left( {a; - b} \right),S - \left( {a;b} \right).\)
Lời giải chi tiết
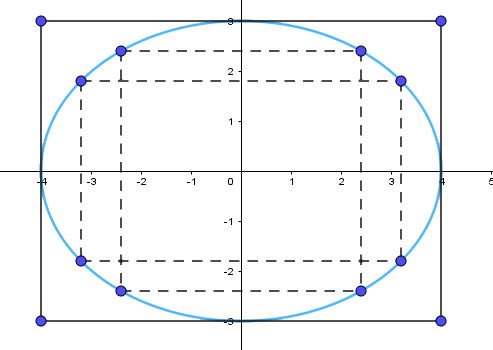
a) Elip nhận ABCD là hình chữ nhật cơ sở nên \(a = 4,b = 3\)
Phương trình chính tắc của elip là \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\)
Để vẽ elip (E), ta có thể làm như sau:
Bước 1: Vẽ hình chữ nhật cơ sở có bốn cạnh thuộc bốn thường thẳng \(x = - 4,x = 4,y = - 3,y = 3\)
Bước 2: Tìm một số điểm cụ thể thuộc elip, chẳng hạn, ta thấy điểm \(M\left( {\frac{{12}}{5};\frac{{12}}{5}} \right)\) và điểm \(N\left( {\frac{{16}}{5};\frac{9}{5}} \right)\) thuộc (E) và điểm \({M_1}\left( {\frac{{12}}{5}; - \frac{{12}}{5}} \right),{M_2}\left( { - \frac{{12}}{5};\frac{{12}}{5}} \right),{M_3}\left( { - \frac{{12}}{5}; - \frac{{12}}{5}} \right),{N_1}\left( {\frac{{16}}{5}; - \frac{9}{5}} \right),{N_3}\left( { - \frac{{16}}{5};\frac{9}{5}} \right),{N_3}\left( { - \frac{{16}}{5}; - \frac{9}{5}} \right)\) thuộc (E)
Bước 3: Vẽ đường elip (E) đi qua các điểm cụ thể trên, nằm ở phía trong hình chữ nhật cơ sở và tiếp xúc với các cạnh của hình chữ nhật cơ sở tại bốn điểm của đỉnh (E) là \({A_1}\left( { - 4;0} \right),{A_1}\left( {4;0} \right),{A_3}\left( {0; - 3} \right),{A_4}\left( {0;3} \right)\)
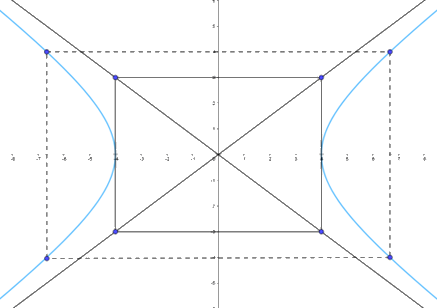
b) Hypebol nhận ABCD là hình chữ nhật cơ sở nên \(a = 4,b = 3\)
Phương trình chính tắc của hypebol là \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)
Để vẽ hypebol (H), ta có thể làm như sau:
Bước 1: Vẽ hình chữ nhật cơ sở có bốn cạnh thuộc bốn thường thẳng \(x = - 4,x = 4,y = - 3,y = 3\)
Bước 2: Vẽ hai đường chéo của hình chữ nhật cơ sở
Tìm một số điểm cụ thể thuộc hypebol, chẳng hạn, ta thấy điểm \(M\left( {\frac{{20}}{3};4} \right)\) thuộc (H) và điểm \({M_1}\left( {\frac{{20}}{3}; - 4} \right),{M_2}\left( { - \frac{{20}}{3};4} \right),{M_3}\left( { - \frac{{20}}{3}; - 4} \right)\) thuộc (H)
Bước 3: Vẽ đường hypebol (H) bên ngoài hình chữ nhật cơ sở, nhánh bên trái tiếp xúc với cạnh của hình chữ nhật cơ sở tại điểm \({A_1}\left( { - 4;0} \right)\) và điểm \({M_2},{M_3}\); nhánh bên phải tiếp xúc với cạnh của hình chữ nhật cơ sở tại điểm \({A_2}\left( {4;0} \right)\) và điểm \(M,{M_1}\). Vẽ các điểm thuộc hypebol càng xa gốc tọa độ thì càng sát với đường tiệm cận. Hypebol nhận gốc tọa độ là tâm đối xứng và hai trục tọa độ là hai trục đối xứng.
Bài 1 trang 66 Chuyên đề học tập Toán 10 – Cánh diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ, phép toán vectơ và ứng dụng của vectơ trong hình học. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các định lý liên quan.
Bài 1 trang 66 thường yêu cầu học sinh thực hiện các thao tác như:
(Ở đây sẽ là lời giải chi tiết cho từng ý của bài 1, bao gồm các bước giải, giải thích rõ ràng và sử dụng các công thức liên quan. Ví dụ:)
Ví dụ: Cho hai vectơ \vec{a} = (1; 2) và \vec{b} = (-3; 4). Tính \vec{a} + \vec{b} và \vec{a} \cdot \vec{b}.
Giải:
Để củng cố kiến thức và kỹ năng giải bài tập, các em có thể tham khảo các bài tập tương tự sau:
Ngoài việc giải các bài tập trong sách giáo khoa, các em có thể tìm hiểu thêm về các ứng dụng của vectơ trong các lĩnh vực khác như vật lý, tin học, đồ họa máy tính. Việc mở rộng kiến thức sẽ giúp các em hiểu sâu sắc hơn về tầm quan trọng và tính ứng dụng của vectơ trong thực tế.
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em sẽ tự tin hơn trong việc giải bài 1 trang 66 Chuyên đề học tập Toán 10 – Cánh diều và các bài tập tương tự. Chúc các em học tập tốt!