Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Trong bài viết này, chúng tôi sẽ cùng nhau giải quyết các bài tập trong mục 2 trang 34 của Chuyên đề học tập Toán 10 - Cánh diều.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong quá trình học tập.
Từ các đẳng thức như
Sử dụng tam giác Pascal để khai triển các biểu thức sau:
a) \({(x + y)^7}\)
b) \({(x - 2)^7}\)
Phương pháp giải:
Tam giác Pascal
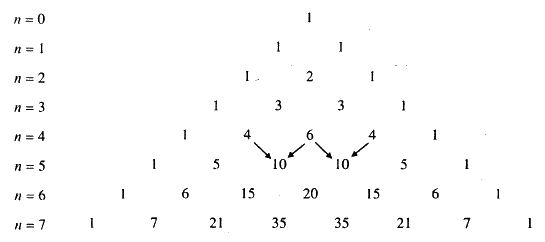
Lời giải chi tiết:
Theo công thức nhị thức Newton, ta có:
\({(3x + 2)^9} = C_9^0{\left( {3x} \right)^9} + C_9^1{\left( {3x} \right)^8}2 + ... + C_9^k{\left( {3x} \right)^{9 - k}}{2^k} + ... + C_9^8\left( {3x} \right){2^8} + C_9^9{2^9}\)
Số hạng chứa \({x^2}\) ứng với \(9 - k = 2\) hay \(k = 7\). Do đó hệ số của \({x^2}\) là
\(C_9^7{3^2}{2^7} = 36.9.128 = 41472\)
Sử dụng tam giác Pascal để khai triển các biểu thức sau:
a) \({(x + y)^7}\)
b) \({(x - 2)^7}\)
Phương pháp giải:
Tam giác Pascal
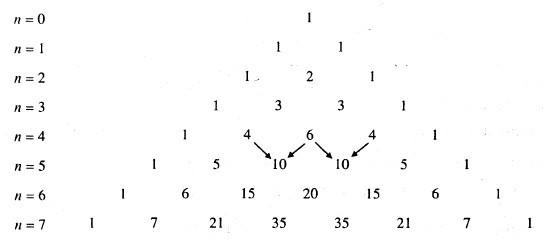
Lời giải chi tiết:
Theo công thức nhị thức Newton, ta có:
\({(3x + 2)^9} = C_9^0{\left( {3x} \right)^9} + C_9^1{\left( {3x} \right)^8}2 + ... + C_9^k{\left( {3x} \right)^{9 - k}}{2^k} + ... + C_9^8\left( {3x} \right){2^8} + C_9^9{2^9}\)
Số hạng chứa \({x^2}\) ứng với \(9 - k = 2\) hay \(k = 7\). Do đó hệ số của \({x^2}\) là
\(C_9^7{3^2}{2^7} = 36.9.128 = 41472\)
Mục 2 trang 34 trong Chuyên đề học tập Toán 10 - Cánh diều thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập, kèm theo các giải thích rõ ràng để bạn hiểu rõ bản chất của vấn đề.
Đề bài: (Giả định một đề bài cụ thể ở đây)
Lời giải:
Giải thích: (Giải thích chi tiết từng bước giải)
Đề bài: (Giả định một đề bài cụ thể ở đây)
Lời giải:
Giải thích: (Giải thích chi tiết từng bước giải)
Đề bài: (Giả định một đề bài cụ thể ở đây)
Lời giải:
(Giải chi tiết bài tập 3)
Giải thích: (Giải thích chi tiết từng bước giải)
Khi giải các bài tập trong mục 2 trang 34 Chuyên đề học tập Toán 10 - Cánh diều, bạn cần lưu ý những điều sau:
Kiến thức được học trong mục 2 trang 34 Chuyên đề học tập Toán 10 - Cánh diều có ứng dụng rộng rãi trong thực tế, ví dụ như:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 2 trang 34 Chuyên đề học tập Toán 10 - Cánh diều. Chúc bạn học tập tốt và đạt kết quả cao!
| Công thức | Mô tả |
|---|---|
| Công thức 1 | Mô tả công thức 1 |
| Công thức 2 | Mô tả công thức 2 |