Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục 5 trang 45, 46 của Chuyên đề học tập Toán 10 - Cánh diều.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho elip (E) \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
Viết phương trình chính tắc của elip, biết tiêu điểm \({F_2}(5;0)\) và đường chuẩn ứng với tiêu điểm đó là \(x = \frac{{36}}{5}.\)
Phương pháp giải:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
+ Tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\)
+ Ứng với tiêu điểm \({F_1}( - c;0)\), có đường chuẩn \({\Delta _1}:x + \frac{a}{e} = 0\)
+ Ứng với tiêu điểm \({F_2}(5;0)\), có đường chuẩn \({\Delta _2}:x - \frac{a}{e} = 0\)
Lời giải chi tiết:
Gọi phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
(E) có tiêu điểm \({F_2}(c;0) = (5;0) \Rightarrow c = 5\)
Ứng với tiêu điểm \({F_2}(3;0)\), có đường chuẩn \({\Delta _2}:x = \frac{a}{e} = \frac{{36}}{5}\)
Mà \(e = \frac{c}{a} = \frac{5}{a} \Rightarrow \frac{a}{e} = \frac{{{a^2}}}{5} = \frac{{36}}{5} \Leftrightarrow {a^2} = 36\) hay \(a = 6\). Suy ra \(b = \sqrt {{a^2} - {c^2}} = \sqrt {{6^2} - {5^2}} = \sqrt {11} \)
Vậy phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{11}} = 1\)
Cho elip (E) \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
Xét đường thẳng \({\Delta _1}:x = - \frac{a}{e}\) với mỗi điểm \(M\left( {x;y} \right) \in \left( E \right)\) (Hình 9), tính:
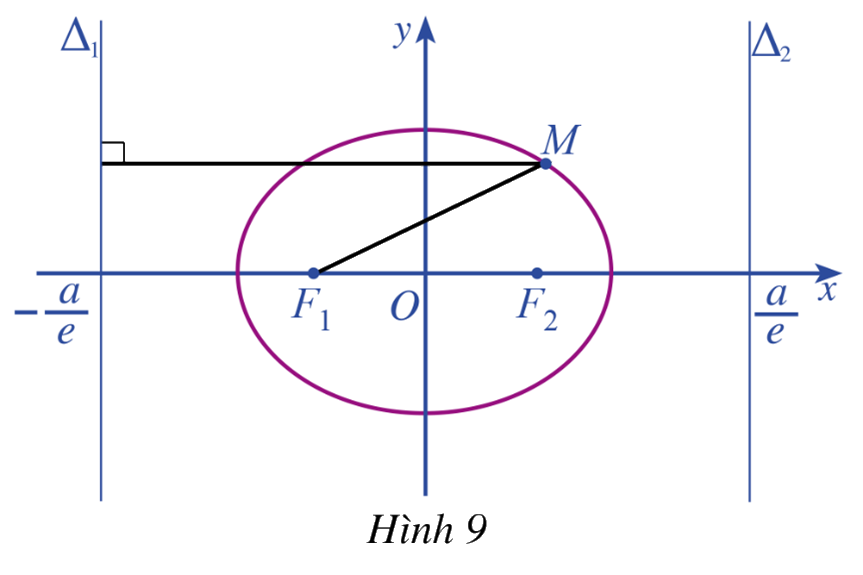
a) Khoảng cách \(d\left( {M,{\Delta _1}} \right)\) từ điểm \(M\left( {x;y} \right)\) đến đường thẳng \({\Delta _1}\)
b) Tỉ số \(\frac{{M{F_1}}}{{d\left( {M,{\Delta _1}} \right)}}\)
Lời giải chi tiết:
a) Viết lại phương trình đưởng thẳng \({\Delta _1}\) ở dạng: \(x + 0y + \frac{a}{e} = 0\)
Với mỗi điểm \(M\left( {x;y} \right) \in \left( E \right)\), ta có: \(d\left( {M,{\Delta _1}} \right) = \frac{{\left| {x + 0y + \frac{a}{e}} \right|}}{{\sqrt {{1^2} + {0^2}} }} = \frac{{\left| {a + ex} \right|}}{e}\)
b) Do \(M{F_1} = a + ex > 0\) nên \(M{F_1} = \left| {a + ex} \right| \Rightarrow d\left( {M,{\Delta _1}} \right) = \frac{{M{F_1}}}{e}\)
Vậy \(\frac{{M{F_1}}}{{d\left( {M,{\Delta _1}} \right)}} = e\)
Viết phương trình chính tắc của elip, biết tiêu điểm \({F_2}(5;0)\) và đường chuẩn ứng với tiêu điểm đó là \(x = \frac{{36}}{5}.\)
Phương pháp giải:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
+ Tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\)
+ Ứng với tiêu điểm \({F_1}( - c;0)\), có đường chuẩn \({\Delta _1}:x + \frac{a}{e} = 0\)
+ Ứng với tiêu điểm \({F_2}(5;0)\), có đường chuẩn \({\Delta _2}:x - \frac{a}{e} = 0\)
Lời giải chi tiết:
Gọi phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
(E) có tiêu điểm \({F_2}(c;0) = (5;0) \Rightarrow c = 5\)
Ứng với tiêu điểm \({F_2}(3;0)\), có đường chuẩn \({\Delta _2}:x = \frac{a}{e} = \frac{{36}}{5}\)
Mà \(e = \frac{c}{a} = \frac{5}{a} \Rightarrow \frac{a}{e} = \frac{{{a^2}}}{5} = \frac{{36}}{5} \Leftrightarrow {a^2} = 36\) hay \(a = 6\). Suy ra \(b = \sqrt {{a^2} - {c^2}} = \sqrt {{6^2} - {5^2}} = \sqrt {11} \)
Vậy phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{11}} = 1\)
Cho elip (E) \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
Xét đường thẳng \({\Delta _1}:x = - \frac{a}{e}\) với mỗi điểm \(M\left( {x;y} \right) \in \left( E \right)\) (Hình 9), tính:
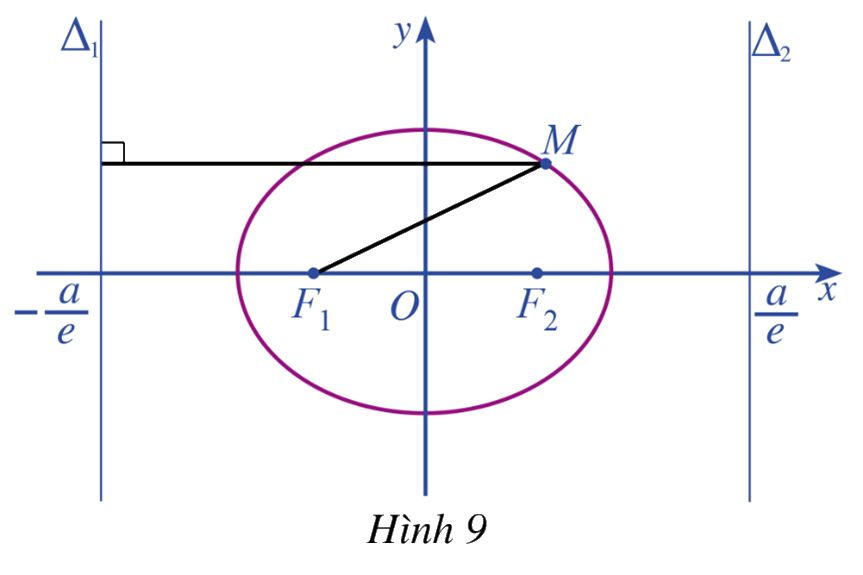
a) Khoảng cách \(d\left( {M,{\Delta _1}} \right)\) từ điểm \(M\left( {x;y} \right)\) đến đường thẳng \({\Delta _1}\)
b) Tỉ số \(\frac{{M{F_1}}}{{d\left( {M,{\Delta _1}} \right)}}\)
Lời giải chi tiết:
a) Viết lại phương trình đưởng thẳng \({\Delta _1}\) ở dạng: \(x + 0y + \frac{a}{e} = 0\)
Với mỗi điểm \(M\left( {x;y} \right) \in \left( E \right)\), ta có: \(d\left( {M,{\Delta _1}} \right) = \frac{{\left| {x + 0y + \frac{a}{e}} \right|}}{{\sqrt {{1^2} + {0^2}} }} = \frac{{\left| {a + ex} \right|}}{e}\)
b) Do \(M{F_1} = a + ex > 0\) nên \(M{F_1} = \left| {a + ex} \right| \Rightarrow d\left( {M,{\Delta _1}} \right) = \frac{{M{F_1}}}{e}\)
Vậy \(\frac{{M{F_1}}}{{d\left( {M,{\Delta _1}} \right)}} = e\)
Mục 5 của Chuyên đề học tập Toán 10 - Cánh diều tập trung vào việc ứng dụng các kiến thức về vectơ trong hình học phẳng. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các định lý, tính chất của vectơ để chứng minh các đẳng thức vectơ, giải quyết các bài toán liên quan đến hình học. Để giải quyết hiệu quả các bài tập này, học sinh cần nắm vững các khái niệm cơ bản về vectơ, phép toán vectơ và các ứng dụng của vectơ trong hình học.
Bài 1 yêu cầu học sinh chứng minh một số đẳng thức vectơ cơ bản. Để giải bài tập này, học sinh cần sử dụng các quy tắc cộng, trừ, nhân vectơ với một số thực và các tính chất của vectơ. Ví dụ, để chứng minh AB + BC = AC, học sinh cần hiểu rằng vectơ AB và BC là các vectơ cạnh của tam giác ABC, và tổng của chúng bằng vectơ AC.
Bài 2 thường yêu cầu học sinh tìm một điểm M thỏa mãn một điều kiện cho trước liên quan đến các vectơ. Để giải bài tập này, học sinh cần sử dụng các phương pháp tọa độ vectơ hoặc các phương pháp hình học. Ví dụ, nếu đề bài yêu cầu tìm điểm M sao cho MA + MB = 0, thì M là trung điểm của đoạn thẳng AB.
Bài 3 thường yêu cầu học sinh sử dụng vectơ để chứng minh các tính chất hình học, chẳng hạn như chứng minh hai đường thẳng song song, chứng minh một điểm nằm trên một đường thẳng, hoặc chứng minh một tứ giác là hình bình hành. Để giải bài tập này, học sinh cần sử dụng các điều kiện tương đương về vectơ để biểu diễn các tính chất hình học.
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong mục 5 trang 45, 46 Chuyên đề học tập Toán 10 - Cánh diều:
Ví dụ: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng MA + MB + MC = 0.
Giải:
Vì M là trung điểm của BC nên MB = MC. Do đó, MA + MB + MC = MA + 2MB. Sử dụng quy tắc trung điểm, ta có MA + MB = AB và MA + MC = AC. Từ đó suy ra MA + MB + MC = 0.
Việc giải các bài tập trong mục 5 trang 45, 46 Chuyên đề học tập Toán 10 - Cánh diều đòi hỏi học sinh phải nắm vững kiến thức về vectơ và vận dụng linh hoạt các phương pháp giải toán. Hy vọng rằng với hướng dẫn chi tiết này, các bạn học sinh sẽ tự tin hơn trong việc giải quyết các bài tập và đạt kết quả tốt nhất trong học tập.