Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 50, 51 Chuyên đề học tập Toán 10 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Chúng tôi hiểu rằng việc học toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã cẩn thận phân tích và giải thích từng bước, đảm bảo các em có thể theo dõi và hiểu rõ quá trình giải.
a) Quan sát điểm \(M\left( {x;y} \right)\) thuộc hypebol (H) (Hình 15) và chứng tỏ rằng \(x \le - a\) hoặc \(x \ge a\)
Viết phương trình chính tắc của hypebol có một đỉnh là \({A_2}\left( {5;0} \right)\) và một đường tiệm cận là \(y = - 3x\)
Phương pháp giải:
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\). Khi đó ta có:
+ 2 đỉnh là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right)\)
+ Hai đường tiệm cận của hypebol (H) lần lượt có phương trình \(y = - \frac{b}{a}x,y = \frac{b}{a}x\)
Lời giải chi tiết:
+ Ta có hypebol có đỉnh \({A_2}(a;0) = \left( {5;0} \right) \Rightarrow a = 5\)
+ Hypebol có đường tiệm cận là \(y = - 3x \Rightarrow \frac{b}{a} = 3 \Rightarrow b = 3a = 15\)
Vậy phương trình hypebol là: \(\frac{{{x^2}}}{{{5^2}}} - \frac{{{y^2}}}{{{{15}^2}}} = 1\)
a) Quan sát điểm \(M\left( {x;y} \right)\) thuộc hypebol (H) (Hình 15) và chứng tỏ rằng \(x \le - a\) hoặc \(x \ge a\)
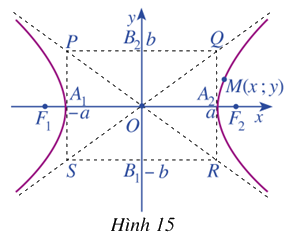
b) Viết phương trình hai đường thẳng PR và QS
Phương pháp giải:
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\). Khi đó ta có:
+ Hình chữ nhật cơ sở có 4 đỉnh \(P\left( { - a;b} \right),Q\left( {a;b} \right),R\left( {a; - b} \right),S - \left( {a;b} \right).\)
+ Hai đường thẳng PR và QS lần lượt có phương trình \(y = - \frac{b}{a}x,y = \frac{b}{a}x\) được gọi là hai đường tiệm cận của hypebol (H)
Lời giải chi tiết:
a) Nếu điểm \(M\left( {x;y} \right)\) thuộc hypebol (H) thì \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
Vì \(\frac{{{y^2}}}{{{b^2}}} \ge 0 \Rightarrow \frac{{{x^2}}}{{{a^2}}} \ge \frac{{{y^2}}}{{{b^2}}} + 1 \Rightarrow {x^2} \ge {a^2} \ge \left[ \begin{array}{l}x \ge a\\x \le - a\end{array} \right.\)
b) Ta có: \(P\left( { - a;b} \right),R\left( {a; - b} \right) \Rightarrow \overrightarrow {PR} = \left( {2a; - 2b} \right)\)
Chọn \(\left( {b;a} \right)\) là 1 vector pháp tuyến của PR, khi đó phương trình đường thẳng PR là: \(PR:b\left( {x + a} \right) + a\left( {y - b} \right) = 0 \Leftrightarrow bx + ay = 0\) hay \(PR:y = - \frac{b}{a}x\)
Ta có: \(Q\left( {a;b} \right),S - \left( {a;b} \right) \Rightarrow \overrightarrow {QS} = \left( { - 2a; - 2b} \right)\)
Chọn \(\left( {b; - a} \right)\) là 1 vector pháp tuyến của QS, khi đó phương trình đường thẳng QS là: \(QS:b\left( {x - a} \right) - a\left( {y - b} \right) = 0 \Leftrightarrow bx - ay = 0\) hay \(QS:y = \frac{b}{a}x\)
a) Quan sát điểm \(M\left( {x;y} \right)\) thuộc hypebol (H) (Hình 15) và chứng tỏ rằng \(x \le - a\) hoặc \(x \ge a\)
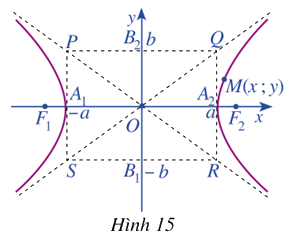
b) Viết phương trình hai đường thẳng PR và QS
Phương pháp giải:
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\). Khi đó ta có:
+ Hình chữ nhật cơ sở có 4 đỉnh \(P\left( { - a;b} \right),Q\left( {a;b} \right),R\left( {a; - b} \right),S - \left( {a;b} \right).\)
+ Hai đường thẳng PR và QS lần lượt có phương trình \(y = - \frac{b}{a}x,y = \frac{b}{a}x\) được gọi là hai đường tiệm cận của hypebol (H)
Lời giải chi tiết:
a) Nếu điểm \(M\left( {x;y} \right)\) thuộc hypebol (H) thì \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
Vì \(\frac{{{y^2}}}{{{b^2}}} \ge 0 \Rightarrow \frac{{{x^2}}}{{{a^2}}} \ge \frac{{{y^2}}}{{{b^2}}} + 1 \Rightarrow {x^2} \ge {a^2} \ge \left[ \begin{array}{l}x \ge a\\x \le - a\end{array} \right.\)
b) Ta có: \(P\left( { - a;b} \right),R\left( {a; - b} \right) \Rightarrow \overrightarrow {PR} = \left( {2a; - 2b} \right)\)
Chọn \(\left( {b;a} \right)\) là 1 vector pháp tuyến của PR, khi đó phương trình đường thẳng PR là: \(PR:b\left( {x + a} \right) + a\left( {y - b} \right) = 0 \Leftrightarrow bx + ay = 0\) hay \(PR:y = - \frac{b}{a}x\)
Ta có: \(Q\left( {a;b} \right),S - \left( {a;b} \right) \Rightarrow \overrightarrow {QS} = \left( { - 2a; - 2b} \right)\)
Chọn \(\left( {b; - a} \right)\) là 1 vector pháp tuyến của QS, khi đó phương trình đường thẳng QS là: \(QS:b\left( {x - a} \right) - a\left( {y - b} \right) = 0 \Leftrightarrow bx - ay = 0\) hay \(QS:y = \frac{b}{a}x\)
Viết phương trình chính tắc của hypebol có một đỉnh là \({A_2}\left( {5;0} \right)\) và một đường tiệm cận là \(y = - 3x\)
Phương pháp giải:
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\). Khi đó ta có:
+ 2 đỉnh là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right)\)
+ Hai đường tiệm cận của hypebol (H) lần lượt có phương trình \(y = - \frac{b}{a}x,y = \frac{b}{a}x\)
Lời giải chi tiết:
+ Ta có hypebol có đỉnh \({A_2}(a;0) = \left( {5;0} \right) \Rightarrow a = 5\)
+ Hypebol có đường tiệm cận là \(y = - 3x \Rightarrow \frac{b}{a} = 3 \Rightarrow b = 3a = 15\)
Vậy phương trình hypebol là: \(\frac{{{x^2}}}{{{5^2}}} - \frac{{{y^2}}}{{{{15}^2}}} = 1\)
Mục 2 của Chuyên đề học tập Toán 10 - Cánh diều tập trung vào các kiến thức về vectơ, bao gồm các khái niệm cơ bản, các phép toán trên vectơ, và ứng dụng của vectơ trong hình học. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương trình toán học ở các lớp trên.
Trang 50 của Chuyên đề học tập Toán 10 - Cánh diều chứa các bài tập rèn luyện về khái niệm vectơ và các phép toán cơ bản. Dưới đây là giải chi tiết một số bài tập tiêu biểu:
Lời giải: Để tìm vectơ c, ta thực hiện phép cộng vectơ a và b theo quy tắc hình bình hành hoặc quy tắc tam giác. Kết quả là vectơ c có điểm đầu là điểm đầu của a và điểm cuối là điểm cuối của b.
Lời giải: Tọa độ của vectơ a được tính theo công thức: x = |a| * cos(α) và y = |a| * sin(α), trong đó |a| là độ dài của vectơ a và α là góc giữa vectơ a và trục x. Thay số vào, ta được x = 5 * cos(30°) ≈ 4.33 và y = 5 * sin(30°) = 2.5. Vậy tọa độ của vectơ a là (4.33, 2.5).
Trang 51 của Chuyên đề học tập Toán 10 - Cánh diều tập trung vào các bài tập ứng dụng của vectơ trong hình học, đặc biệt là trong việc chứng minh các tính chất của hình bình hành, hình chữ nhật, hình thoi, và hình vuông.
Lời giải: Theo định nghĩa của hình bình hành, hai cạnh đối song song và bằng nhau. Do đó, AB = DC và AD = BC.
Lời giải: Xét hai tam giác vuông ABC và ADC. Ta có: AB = CD (cạnh đối của hình chữ nhật), BC = AD (cạnh đối của hình chữ nhật), và ∠ABC = ∠ADC = 90°. Do đó, tam giác ABC bằng tam giác ADC (cạnh - góc - cạnh). Suy ra, AC = BD.
Hy vọng với lời giải chi tiết và những lời khuyên trên, các em sẽ tự tin hơn khi giải các bài tập về vectơ trong Chuyên đề học tập Toán 10 - Cánh diều. Chúc các em học tốt!