Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải quyết các bài tập trong mục 1 trang 60 của Chuyên đề học tập Toán 10 - Cánh diều.
Chúng tôi hiểu rằng việc học toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải chính xác, rõ ràng và dễ tiếp thu nhất.
Quan sát Hình 22a, Hình 22b, Hình 22c và nêu tỉ số khoảng cách từ một điểm M nằm trên mỗi đường conic đến tiêu điểm của nó và khoảng cách từ điểm M đến đường chuẩn tương ứng với tiêu điểm đó.
Đề bài
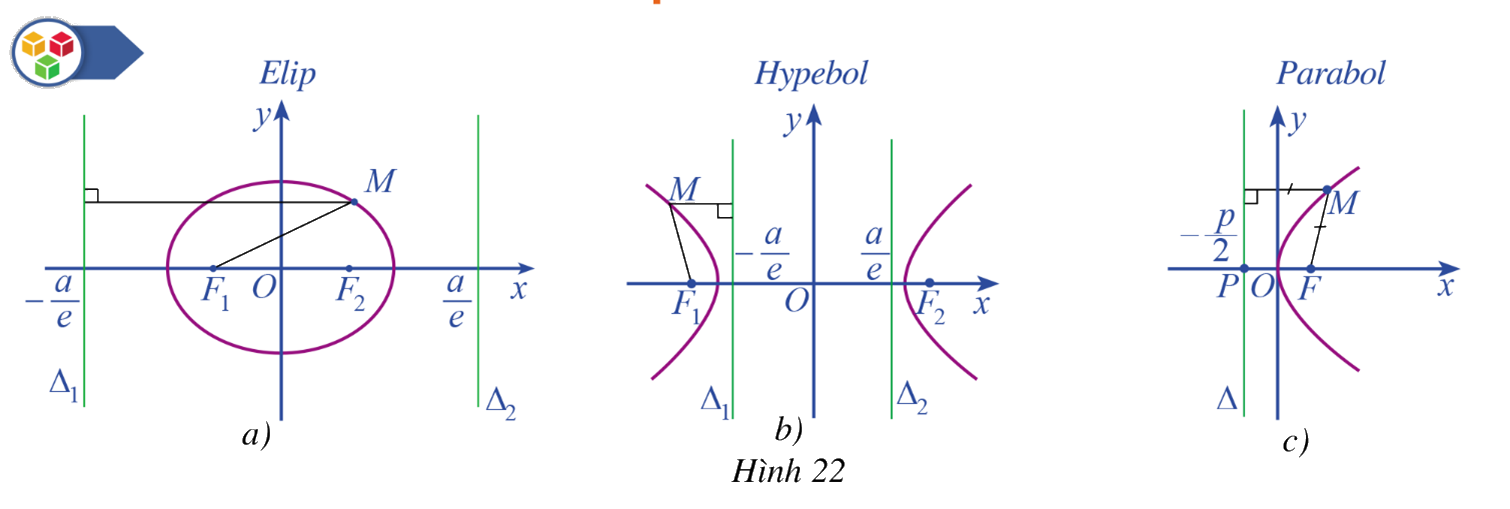
Quan sát Hình 22a, Hình 22b, Hình 22c và nêu tỉ số khoảng cách từ một điểm M nằm trên mỗi đường conic đến tiêu điểm của nó và khoảng cách từ điểm M đến đường chuẩn tương ứng với tiêu điểm đó.
Lời giải chi tiết
+ Với mọi điểm M thuộc elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > b > 0} \right)\), ta luôn có \(\frac{{MF}}{{d\left( {M,\Delta } \right)}} = e\left( {0 < e < 1} \right)\), trong đó F là một trong hai tiêu điểm \({F_1},{F_2}\) và \(\Delta \) là đường chuẩn ứng tiêu điểm F
+ Với mọi điểm M thuộc hypebol (H): \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > 0,b > 0} \right)\), ta luôn có \(\frac{{MF}}{{d\left( {M,\Delta } \right)}} = e\left( {e > 1} \right)\), trong đó F là một trong hai tiêu điểm \({F_1},{F_2}\) và \(\Delta \) là đường chuẩn ứng tiêu điểm F
+ Với mọi điểm M thuộc parabol (P): \({y^2} = 2px\left( {p > 0} \right)\), ta luôn có \(\frac{{MF}}{{d\left( {M,\Delta } \right)}} = 1\), trong đó F là một trong hai tiêu điểm \({F_1},{F_2}\) và \(\Delta \) là đường chuẩn ứng tiêu điểm F
Mục 1 trang 60 trong Chuyên đề học tập Toán 10 - Cánh diều thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững kiến thức lý thuyết liên quan, hiểu rõ các định nghĩa, định lý và công thức đã học. Bài viết này sẽ đi sâu vào phân tích từng bài tập, cung cấp lời giải chi tiết và các bước thực hiện cụ thể.
Thông thường, Mục 1 trang 60 sẽ bao gồm các dạng bài tập sau:
Đề bài: Cho hàm số y = f(x) = 2x + 1. Tính f(0), f(1), f(-1).
Lời giải:
Đề bài: Chứng minh rằng (a + b)^2 = a^2 + 2ab + b^2.
Lời giải:
(a + b)^2 = (a + b) * (a + b) = a * a + a * b + b * a + b * b = a^2 + ab + ab + b^2 = a^2 + 2ab + b^2.
Đề bài: Giải phương trình 2x + 3 = 7.
Lời giải:
2x = 7 - 3 = 4
x = 4 / 2 = 2
Để giải các bài tập trong Mục 1 trang 60 Chuyên đề học tập Toán 10 - Cánh diều một cách hiệu quả, bạn nên:
Ngoài sách giáo khoa và sách bài tập, bạn có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong Mục 1 trang 60 Chuyên đề học tập Toán 10 - Cánh diều. Chúc bạn học tập tốt và đạt kết quả cao!