Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục 6 trang 46 của Chuyên đề học tập Toán 10 - Cánh diều.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho elip (E) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
Cho elip (E) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
Xét đường tròn (C) tâm O bán kính a có phương trình \({x^2} + {y^2} = {a^2}\)
Cét điểm \(M\left( {x;y} \right) \in \left( E \right)\) và \({M_1}\left( {x;{y_1}} \right) \in \left( C \right)\) sao cho \(y\) và \({y_1}\) luôn cùng dấu (Khi M khác với hai đỉnh \({A_1},{A_2}\) của (E)) (Hình 10)
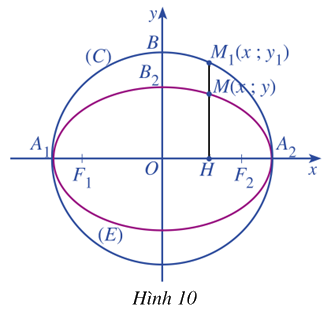
a) Từ phương trình chính tắc của elip (E), hãy tính \({y^2}\) theo \({x^2}\)
Từ phương trình của đường tròn (C), hãy tính \({y_1}^2\) theo \({x^2}\)
b) Tính tỉ số \(\frac{{HM}}{{H{M_1}}} = \frac{y}{{{y_1}}}\) theo \(a,b\)
Lời giải chi tiết:
a) Ta có \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1 \Rightarrow {y^2} = {b^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right) = \frac{{\left( {{a^2} - {x^2}} \right){b^2}}}{{{a^2}}}\)
Tương tự, \({M_1}\left( {x;{y_1}} \right) \in \left( C \right)\) nên \({x^2} + {y_1}^2 = {a^2} \Rightarrow {y_1}^2 = {a^2} - {x^2}\)
b) Ta có: \(\frac{{{y^2}}}{{{y_1}^2}} = \frac{{\frac{{\left( {{a^2} - {x^2}} \right){b^2}}}{{{a^2}}}}}{{{a^2} - {x^2}}} = \frac{{{b^2}}}{{{a^2}}}\).
Vậy \(\frac{{HM}}{{H{M_1}}} = \frac{y}{{{y_1}}} = \frac{b}{a}\), tức là \({y_1} = \frac{a}{b}y\)
Cho elip (E) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
Xét đường tròn (C) tâm O bán kính a có phương trình \({x^2} + {y^2} = {a^2}\)
Cét điểm \(M\left( {x;y} \right) \in \left( E \right)\) và \({M_1}\left( {x;{y_1}} \right) \in \left( C \right)\) sao cho \(y\) và \({y_1}\) luôn cùng dấu (Khi M khác với hai đỉnh \({A_1},{A_2}\) của (E)) (Hình 10)
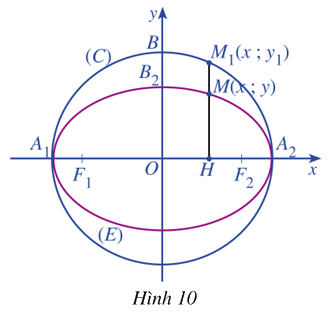
a) Từ phương trình chính tắc của elip (E), hãy tính \({y^2}\) theo \({x^2}\)
Từ phương trình của đường tròn (C), hãy tính \({y_1}^2\) theo \({x^2}\)
b) Tính tỉ số \(\frac{{HM}}{{H{M_1}}} = \frac{y}{{{y_1}}}\) theo \(a,b\)
Lời giải chi tiết:
a) Ta có \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1 \Rightarrow {y^2} = {b^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right) = \frac{{\left( {{a^2} - {x^2}} \right){b^2}}}{{{a^2}}}\)
Tương tự, \({M_1}\left( {x;{y_1}} \right) \in \left( C \right)\) nên \({x^2} + {y_1}^2 = {a^2} \Rightarrow {y_1}^2 = {a^2} - {x^2}\)
b) Ta có: \(\frac{{{y^2}}}{{{y_1}^2}} = \frac{{\frac{{\left( {{a^2} - {x^2}} \right){b^2}}}{{{a^2}}}}}{{{a^2} - {x^2}}} = \frac{{{b^2}}}{{{a^2}}}\).
Vậy \(\frac{{HM}}{{H{M_1}}} = \frac{y}{{{y_1}}} = \frac{b}{a}\), tức là \({y_1} = \frac{a}{b}y\)
Mục 6 trang 46 trong Chuyên đề học tập Toán 10 - Cánh diều thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững kiến thức lý thuyết liên quan, hiểu rõ các định nghĩa, định lý và công thức quan trọng. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập, kèm theo các giải thích rõ ràng và dễ hiểu.
Trước khi đi vào giải bài tập, chúng ta cần xác định nội dung chính của Mục 6. Thông thường, mục này sẽ đề cập đến một trong các chủ đề sau:
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 6 trang 46 Chuyên đề học tập Toán 10 - Cánh diều. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng và dễ hiểu, giúp bạn có thể tự giải các bài tập tương tự.
Đề bài: Giải phương trình bậc hai 2x2 - 5x + 3 = 0
Lời giải:
Đề bài: Tìm điều kiện để phương trình ax2 + bx + c = 0 có nghiệm kép.
Lời giải:
Phương trình ax2 + bx + c = 0 có nghiệm kép khi và chỉ khi delta bằng 0: Δ = b2 - 4ac = 0
Đề bài: Giải bất phương trình bậc hai x2 - 4x + 3 > 0
Lời giải:
Để giải bài tập trong Mục 6 trang 46 Chuyên đề học tập Toán 10 - Cánh diều một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những lời giải chi tiết và hữu ích cho các bài tập trong Mục 6 trang 46 Chuyên đề học tập Toán 10 - Cánh diều. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!