Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải quyết các bài tập trong mục 2 trang 58 của Chuyên đề học tập Toán 10 - Cánh diều.
Chúng tôi hiểu rằng việc học toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải chính xác, rõ ràng và dễ tiếp thu nhất.
Trong mặt phẳng tọa độ \(Oxy\), ta xét parabol (P) với phương trình chính tắc \({y^2} = 2px\) trong đó \(p > 0\) (Hình 20)
a) Lập phương trình chính tắc của parabol (P), biết phương trình đường chuẩn là \(x = - 2\)
b) Tìm tọa độ tiêu điểm của parabol (P)
c) Tìm tọa độ điểm M thuộc parabol (P), biết khoảng cách từ M đến tiêu điểm bằng 6
Phương pháp giải:
Cho parabol có PTCT: \({y^2} = 2px\) trong đó \(p > 0\)
+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)
+ Đường chuẩn: \(\Delta :x = - \frac{p}{2}\)
Lời giải chi tiết:
a) Ta có phương trình đường chuẩn \(x = - 2 \Rightarrow \frac{p}{2} = 2 \Rightarrow p = 4\)
Vậy phương trình chính tắc của parabol (P) là \({y^2} = 8x\)
b) Tiêu điểm của parabol (P) là \(F\left( {2;0} \right)\)
c) Khoảng cách từ M đến tiêu điểm \(F\left( {2;0} \right)\) bằng 6 nên \(x + \frac{p}{2} = 6 \Rightarrow x + 2 = 6 \Rightarrow x = 4 \Rightarrow {y^2} = 8.4 \Rightarrow y = \pm 4\sqrt 2 \)
Vậy \(M\left( {4; \pm 4\sqrt 2 } \right)\)
Trong mặt phẳng tọa độ \(Oxy\), ta xét parabol (P) với phương trình chính tắc \({y^2} = 2px\) trong đó \(p > 0\) (Hình 20)
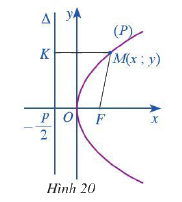
a) So sánh khoảng cách từ MF từ điểm M đến tiêu điểm F và khoảng cách MK từ điểm M đến đường thẳng \(\Delta \)
b) Tính độ dài đoạn thẳng MK. Từ đó tính độ dài đoạn thẳng MF
Phương pháp giải:
Cho parabol có PTCT: \({y^2} = 2px\) trong đó \(p > 0\)
+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)
+ Đường chuẩn: \(\Delta :x = - \frac{p}{2}\)
Lời giải chi tiết:
a) Khoảng cách MF từ điểm M đến tiêu điểm F bằng khoảng cách MK từ điểm M đến đường chuẩn \(\Delta \)
b) Ta có
\(MF = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \sqrt {{x^2} - px + \frac{{{p^2}}}{4} + 2px} = \sqrt {{x^2} + px + \frac{{{p^2}}}{4}} = \sqrt {{{\left( {x + \frac{p}{2}} \right)}^2}} = x + \frac{p}{2}\)
Phương trình đường chuẩn \(\Delta :x = - \frac{p}{2} \Rightarrow \Delta :x + 0y + \frac{p}{2} = 0\)
Khoảng cách MK từ điểm M đến đường thẳng \(\Delta \) là: \(MK = \frac{{\left| {x + 0y + \frac{p}{2}} \right|}}{{\sqrt {{1^2} + {0^2}} }} = \left| {x + \frac{p}{2}} \right| = x + \frac{p}{2}\)
Vậy \(MF = MK = x + \frac{p}{2}\)
Trong mặt phẳng tọa độ \(Oxy\), ta xét parabol (P) với phương trình chính tắc \({y^2} = 2px\) trong đó \(p > 0\) (Hình 20)
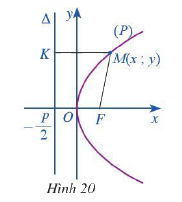
a) So sánh khoảng cách từ MF từ điểm M đến tiêu điểm F và khoảng cách MK từ điểm M đến đường thẳng \(\Delta \)
b) Tính độ dài đoạn thẳng MK. Từ đó tính độ dài đoạn thẳng MF
Phương pháp giải:
Cho parabol có PTCT: \({y^2} = 2px\) trong đó \(p > 0\)
+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)
+ Đường chuẩn: \(\Delta :x = - \frac{p}{2}\)
Lời giải chi tiết:
a) Khoảng cách MF từ điểm M đến tiêu điểm F bằng khoảng cách MK từ điểm M đến đường chuẩn \(\Delta \)
b) Ta có
\(MF = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \sqrt {{x^2} - px + \frac{{{p^2}}}{4} + 2px} = \sqrt {{x^2} + px + \frac{{{p^2}}}{4}} = \sqrt {{{\left( {x + \frac{p}{2}} \right)}^2}} = x + \frac{p}{2}\)
Phương trình đường chuẩn \(\Delta :x = - \frac{p}{2} \Rightarrow \Delta :x + 0y + \frac{p}{2} = 0\)
Khoảng cách MK từ điểm M đến đường thẳng \(\Delta \) là: \(MK = \frac{{\left| {x + 0y + \frac{p}{2}} \right|}}{{\sqrt {{1^2} + {0^2}} }} = \left| {x + \frac{p}{2}} \right| = x + \frac{p}{2}\)
Vậy \(MF = MK = x + \frac{p}{2}\)
a) Lập phương trình chính tắc của parabol (P), biết phương trình đường chuẩn là \(x = - 2\)
b) Tìm tọa độ tiêu điểm của parabol (P)
c) Tìm tọa độ điểm M thuộc parabol (P), biết khoảng cách từ M đến tiêu điểm bằng 6
Phương pháp giải:
Cho parabol có PTCT: \({y^2} = 2px\) trong đó \(p > 0\)
+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)
+ Đường chuẩn: \(\Delta :x = - \frac{p}{2}\)
Lời giải chi tiết:
a) Ta có phương trình đường chuẩn \(x = - 2 \Rightarrow \frac{p}{2} = 2 \Rightarrow p = 4\)
Vậy phương trình chính tắc của parabol (P) là \({y^2} = 8x\)
b) Tiêu điểm của parabol (P) là \(F\left( {2;0} \right)\)
c) Khoảng cách từ M đến tiêu điểm \(F\left( {2;0} \right)\) bằng 6 nên \(x + \frac{p}{2} = 6 \Rightarrow x + 2 = 6 \Rightarrow x = 4 \Rightarrow {y^2} = 8.4 \Rightarrow y = \pm 4\sqrt 2 \)
Vậy \(M\left( {4; \pm 4\sqrt 2 } \right)\)
Mục 2 trang 58 trong Chuyên đề học tập Toán 10 - Cánh diều thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững kiến thức lý thuyết liên quan, hiểu rõ các định nghĩa, định lý và công thức đã học. Bài viết này sẽ đi sâu vào phân tích từng bài tập, cung cấp lời giải chi tiết và giải thích rõ ràng các bước thực hiện.
Bài 1 trong mục 2 thường là bài tập áp dụng trực tiếp các kiến thức lý thuyết đã học. Để giải bài này, bạn cần:
Ví dụ, nếu bài toán yêu cầu tính độ dài của một đoạn thẳng, bạn cần áp dụng công thức tính độ dài đoạn thẳng và thay các giá trị đã cho vào công thức để tìm ra kết quả.
Bài 2 thường là bài tập nâng cao, đòi hỏi học sinh phải vận dụng kiến thức đã học để giải quyết các vấn đề phức tạp hơn. Để giải bài này, bạn cần:
Ví dụ, nếu bài toán yêu cầu chứng minh một đẳng thức, bạn cần sử dụng các phép biến đổi tương đương để đưa đẳng thức về dạng đơn giản hơn và chứng minh tính đúng đắn của nó.
Bài 3 thường là bài tập ứng dụng, liên hệ với các tình huống thực tế. Để giải bài này, bạn cần:
Ví dụ, nếu bài toán yêu cầu tính diện tích của một mảnh đất hình chữ nhật, bạn cần đo đạc các kích thước của mảnh đất và áp dụng công thức tính diện tích hình chữ nhật để tìm ra kết quả.
Để giải bài tập Toán 10 hiệu quả, bạn cần lưu ý một số điều sau:
Giải mục 2 trang 58 Chuyên đề học tập Toán 10 - Cánh diều đòi hỏi sự nắm vững kiến thức lý thuyết, kỹ năng giải toán và sự kiên trì. Hy vọng rằng với những hướng dẫn chi tiết và lời giải cụ thể trong bài viết này, bạn sẽ tự tin hơn trong việc giải quyết các bài tập Toán 10 và đạt được kết quả tốt nhất.
| Công thức | Mô tả |
|---|---|
| Độ dài đoạn thẳng | AB = √( (xB - xA)2 + (yB - yA)2 ) |
| Diện tích hình chữ nhật | S = a * b |