Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 2 trang 59 trong Chuyên đề học tập Toán 10 – Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
Trong mặt phẳng tọa độ Oxy, cho parabol có phương trình chính tắc là \({y^2} = 8x\)
Đề bài
Trong mặt phẳng tọa độ Oxy, cho parabol có phương trình chính tắc là \({y^2} = 8x\)
a) Xác định tọa độ tiêu điểm và phương trình đường chuẩn của parabol
b) Vẽ parabol
Phương pháp giải - Xem chi tiết
Cho parabol có PTCT: \({y^2} = 2px\) trong đó \(p > 0\)
+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)
+ Đường chuẩn: \(\Delta :x = - \frac{p}{2}\)
Lời giải chi tiết
a) Ta có: \(2p = 8 \Rightarrow p = 4\)
Tiêu điểm của parabol (P) là \(F\left( {2;0} \right)\)
Đường chuẩn: \(\Delta :x = - 2\)
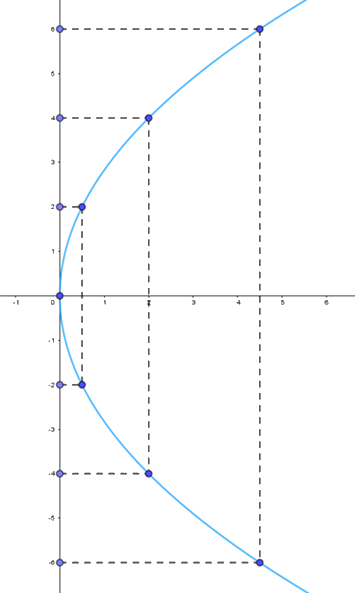
b) Vẽ parabol
Để vẽ parabol (P): \({y^2} = 4x\) ta có thể làm như sau:
Bước 1: Lập bảng giá trị
x | 0 | 0,5 | 0,5 | 2 | 2 | 4,5 | 4,5 |
y | 0 | -2 | 2 | -4 | 4 | -6 | 6 |
Chú ý rằng tương ứng với mỗi giá trị dương của x có hai giá trị của y đối nhau
Bước 2: Vẽ các điểm cụ thể mà hoành độ và tung độ được xác định như trong bảng giá trị
Bước 3: Vẽ đường parabol bên phải trục Oy, đỉnh O, trục đối xứng là Ox, parabol đi qua các điểm được vẽ ở Bước 2
Bài 2 trang 59 Chuyên đề học tập Toán 10 – Cánh diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ trong không gian để giải quyết các bài toán hình học. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, các phép toán vectơ và các ứng dụng của vectơ trong hình học.
Trước khi bắt đầu giải bài tập, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 2 trang 59, yêu cầu thường là chứng minh một đẳng thức vectơ, tìm một điểm thỏa mãn một điều kiện nào đó, hoặc tính độ dài của một đoạn thẳng, góc giữa hai vectơ. Việc xác định đúng yêu cầu của bài toán sẽ giúp bạn lựa chọn phương pháp giải phù hợp.
(Lưu ý: Nội dung lời giải chi tiết sẽ thay đổi tùy thuộc vào từng dạng bài cụ thể trong bài 2 trang 59. Dưới đây là một ví dụ minh họa.)
Bài toán: Cho hình hộp ABCD.A'B'C'D'. Gọi M là trung điểm của cạnh AB. Chứng minh rằng vectơ MM' vuông góc với mặt phẳng (ABCD).
Lời giải:
Bài 2 trang 59 thường xuất hiện các dạng bài tập sau:
Để giải bài tập vectơ nhanh và hiệu quả, bạn có thể áp dụng một số mẹo sau:
Bài 2 trang 59 Chuyên đề học tập Toán 10 – Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ trong không gian. Hy vọng với hướng dẫn chi tiết và các mẹo giải nhanh trên, bạn sẽ giải bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!