Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 39, 40 Chuyên đề học tập Toán 10 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Chúng tôi hiểu rằng việc học toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn các lời giải chi tiết, kèm theo các lưu ý quan trọng để giúp các em hiểu sâu sắc hơn về bài học.
Trong mặt phẳng tọa độ \(Oxy\), ta xét Elip \(\left( E \right)\) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\) (Hình 2)
Trong mặt phẳng tọa độ \(Oxy\), ta xét Elip \(\left( E \right)\) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\)
Cho điểm \(M\left( {x;y} \right)\) nẳm trên \(\left( E \right)\) (Hình 3)
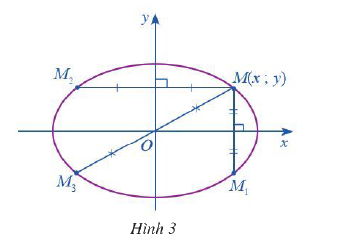
a) Gọi \({M_1}\) là điểm đối xứng của M qua trục Ox. Tìm tọa độ của điểm \({M_1}\). Điểm \({M_1}\) có nằm trên \(\left( E \right)\) hay không? Tại sao?
b) Gọi \({M_2}\) là điểm đối xứng của M qua trục Oy. Tìm tọa độ của điểm \({M_2}\). Điểm \({M_2}\) có nằm trên \(\left( E \right)\) hay không? Tại sao?
c) Gọi \({M_3}\) là điểm đối xứng của M qua gốc O. Tìm tọa độ của điểm \({M_3}\). Điểm \({M_3}\) có nằm trên \(\left( E \right)\) hay không? Tại sao?
Lời giải chi tiết:
a) Điểm \({M_1}\) là điểm đối xứng của M qua trục Ox, nên \({M_1}\left( {x; - y} \right)\)
\({M_1}\left( {x; - y} \right)\) thuộc Elip vì \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{{( - y)}^2}}}{{{b^2}}} = \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
b) Điểm \({M_2}\) là điểm đối xứng của M qua trục Oy, nên \({M_2}\left( { - x;y} \right)\)
\({M_2}\left( { - x;y} \right)\) thuộc Elip vì \(\frac{{{{( - x)}^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
c) Điểm \({M_3}\) là điểm đối xứng của M qua gốc O, nên \({M_3}\left( { - x; - y} \right)\)
\({M_3}\left( { - x; - y} \right)\) thuộc Elip vì \(\frac{{{{( - x)}^2}}}{{{a^2}}} + \frac{{{{( - y)}^2}}}{{{b^2}}} = \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Trong mặt phẳng tọa độ \(Oxy\), ta xét Elip \(\left( E \right)\) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\) (Hình 2)
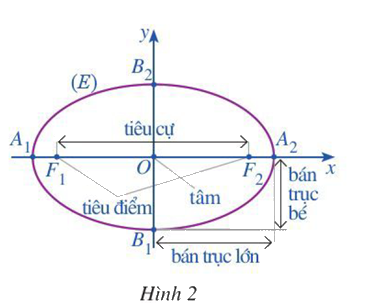
a) Tìm tọa độ của hai tiêu điểm \({F_1},{F_2}\) của \(\left( E \right)\)
b) \(\left( E \right)\) cắt trục \(Ox\) tịa các điểm \({A_1},{A_2}\) và cắt trục \(Oy\) tịa các điểm \({B_1},{B_2}\). Tìm độ dài các đoạn thẳng \(O{A_2},O{B_2}\)
Phương pháp giải:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
+ 4 đỉnh là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right).\)
Lời giải chi tiết:
Elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\) có 4 đỉnh \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right).\)
\( \Rightarrow O{A_2} = a;O{B_2} = b\)
Trong mặt phẳng tọa độ \(Oxy\), ta xét Elip \(\left( E \right)\) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\) (Hình 2)
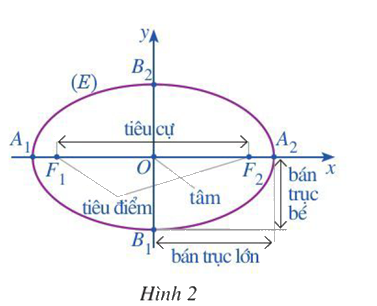
a) Tìm tọa độ của hai tiêu điểm \({F_1},{F_2}\) của \(\left( E \right)\)
b) \(\left( E \right)\) cắt trục \(Ox\) tịa các điểm \({A_1},{A_2}\) và cắt trục \(Oy\) tịa các điểm \({B_1},{B_2}\). Tìm độ dài các đoạn thẳng \(O{A_2},O{B_2}\)
Phương pháp giải:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
+ 4 đỉnh là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right).\)
Lời giải chi tiết:
Elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\) có 4 đỉnh \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right).\)
\( \Rightarrow O{A_2} = a;O{B_2} = b\)
Trong mặt phẳng tọa độ \(Oxy\), ta xét Elip \(\left( E \right)\) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó \(a > b > 0\)
Cho điểm \(M\left( {x;y} \right)\) nẳm trên \(\left( E \right)\) (Hình 3)
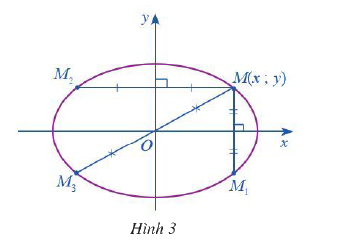
a) Gọi \({M_1}\) là điểm đối xứng của M qua trục Ox. Tìm tọa độ của điểm \({M_1}\). Điểm \({M_1}\) có nằm trên \(\left( E \right)\) hay không? Tại sao?
b) Gọi \({M_2}\) là điểm đối xứng của M qua trục Oy. Tìm tọa độ của điểm \({M_2}\). Điểm \({M_2}\) có nằm trên \(\left( E \right)\) hay không? Tại sao?
c) Gọi \({M_3}\) là điểm đối xứng của M qua gốc O. Tìm tọa độ của điểm \({M_3}\). Điểm \({M_3}\) có nằm trên \(\left( E \right)\) hay không? Tại sao?
Lời giải chi tiết:
a) Điểm \({M_1}\) là điểm đối xứng của M qua trục Ox, nên \({M_1}\left( {x; - y} \right)\)
\({M_1}\left( {x; - y} \right)\) thuộc Elip vì \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{{( - y)}^2}}}{{{b^2}}} = \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
b) Điểm \({M_2}\) là điểm đối xứng của M qua trục Oy, nên \({M_2}\left( { - x;y} \right)\)
\({M_2}\left( { - x;y} \right)\) thuộc Elip vì \(\frac{{{{( - x)}^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
c) Điểm \({M_3}\) là điểm đối xứng của M qua gốc O, nên \({M_3}\left( { - x; - y} \right)\)
\({M_3}\left( { - x; - y} \right)\) thuộc Elip vì \(\frac{{{{( - x)}^2}}}{{{a^2}}} + \frac{{{{( - y)}^2}}}{{{b^2}}} = \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Mục 1 của Chuyên đề học tập Toán 10 - Cánh diều tập trung vào các kiến thức cơ bản về vectơ, bao gồm định nghĩa, các phép toán trên vectơ, và ứng dụng của vectơ trong hình học. Việc nắm vững các khái niệm này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Trang 39 tập trung vào các bài tập vận dụng định nghĩa vectơ và các phép toán cơ bản. Các bài tập thường yêu cầu học sinh:
Bài 1: Cho tam giác ABC. Tìm vectơ biểu diễn cạnh BC.
Lời giải: Vectơ biểu diễn cạnh BC là BC.
Trang 40 nâng cao độ khó với các bài tập liên quan đến ứng dụng của vectơ trong hình học. Các bài tập thường yêu cầu học sinh:
Bài 2: Cho ba điểm A, B, C không thẳng hàng. Gọi M là trung điểm của BC. Chứng minh rằng AM = (AB + AC)/2.
Lời giải:
Ta có: AB + AC = 2AM (quy tắc trung điểm). Do đó, AM = (AB + AC)/2.
Để giải các bài tập về vectơ hiệu quả, học sinh cần:
Khi giải các bài tập về vectơ, cần chú ý đến chiều của vectơ và hướng của vectơ. Việc nhầm lẫn về chiều và hướng có thể dẫn đến kết quả sai.
Hy vọng rằng với lời giải chi tiết và phương pháp giải hiệu quả này, các em học sinh sẽ tự tin hơn khi giải các bài tập về vectơ trong Chuyên đề học tập Toán 10 - Cánh diều. Chúc các em học tập tốt!
| Bài tập | Trang | Mức độ khó |
|---|---|---|
| Bài 1 | 39 | Dễ |
| Bài 2 | 40 | Trung bình |