Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Chúng tôi tập trung vào việc hỗ trợ học sinh nắm vững kiến thức và kỹ năng giải toán một cách hiệu quả.
Ở trang này, bạn sẽ tìm thấy đáp án và lời giải cho các bài tập trong mục 1 của Chuyên đề học tập Toán 10 - Cánh diều, cụ thể là các trang 23, 24 và 25.
Chia hình vuông cạnh 1 thành 4 hình vuông nhỏ bằng nhau, lấy ra hình vuông nhỏ thứ nhất (ở góc dưới bên trái, màu đỏ), cạnh của hình vuông đó bằng (frac{1}{2}.)
Xét mệnh đề chứa biến P(n): “\(1 + 3 + 5 + ... + (2n - 1) = {n^2}\)” với n là số nguyên dương.
a) Chứng tỏ rằng P(1) là mệnh đề đúng.
b) Với k là một số nguyên dương tùy ý mà P(k) là mệnh đề đúng, cho biết \(1 + 3 + 5 + ... + (2k - 1)\) bằng bao nhiêu.
c) Với k là một số nguyên dương tùy ý mà P(k) là mệnh đề đúng, chứng tỏ rằng P(k+1) cũng là mệnh đề đúng bằng cách chỉ ra \({k^2} + [2(k + 1) - 1] = {(k + 1)^2}\).
Lời giải chi tiết:
a) Mệnh đề P(1) là: “\(1 = {1^2}\)”, rõ ràng mệnh đề này đúng.
b) Mệnh đề P(k) là: “\(1 + 3 + 5 + ... + (2k - 1) = {k^2}\)”
Mệnh đề P(k) đúng thì \(1 + 3 + 5 + ... + (2k - 1)\) bằng \({k^2}\)
c) Mệnh đề P(k+1) là: “\(1 + 3 + 5 + ... + [2(k + 1) - 1] = {(k + 1)^2}\)”
Mệnh đề P(k) đúng nên ta có \(1 + 3 + 5 + ... + (2k - 1) = {k^2}\)
\(\begin{array}{l} \Rightarrow 1 + 3 + 5 + ... + [2(k + 1) - 1] = 1 + 3 + 5 + ... + (2k - 1) + [2(k + 1) - 1]\\ = {k^2} + [2(k + 1) - 1] = {k^2} + 2k + 1 = {(k + 1)^2}\end{array}\)
Vậy mệnh đề P(k+1) cũng đúng.
Chứng minh:
a) \(\frac{1}{{\sqrt 1 + \sqrt 2 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }} + ... + \frac{1}{{\sqrt n + \sqrt {n + 1} }} = \sqrt {n + 1} - 1\) với mọi \(n \in \mathbb{N}*\)
b) \(\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{n^3} - 1}}{{{n^3} + 1}} = \frac{{2({n^2} + n + 1)}}{{3n(n + 1)}}\) với mọi \(n \in \mathbb{N}*,n \ge 2\)
Phương pháp giải:
Chứng minh mệnh đề P(n) đúng với \(n \ge p\) thì:
Bước 1: Chứng tỏ mệnh đề đúng với \(n = p\)
Bước 2: Với k là một số nguyên dương tùy ý mà P(k) là mệnh đề đúng, ta chứng tỏ P(k+1) cũng là mệnh đề đúng.
Lời giải chi tiết:
a) Ta chứng minh bằng quy nạp theo n.
Bước 1: Khi \(n = 1\) ta có \(\frac{1}{{\sqrt 1 + \sqrt 2 }} = \sqrt 2 - 1\), đúng
vì \(\left( {\sqrt 2 + \sqrt 1 } \right)\left( {\sqrt 2 - \sqrt 1 } \right) = 2 - 1 = 1 \Rightarrow \frac{1}{{\sqrt 2 + \sqrt 1 }} = \sqrt 2 - \sqrt 1 = \sqrt 2 - 1\)
Như vậy đẳng thức đúng với \(n = 1\)
Bước 2: Với k là một số nguyên dương tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức đúng với k+1, tức là:
\(\frac{1}{{\sqrt 1 + \sqrt 2 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }} + ... + \frac{1}{{\sqrt {k + 1} + \sqrt {k + 2} }} = \sqrt {k + 2} - 1\)
Thật vậy, theo giả thiết quy nạp ta có:
\(\frac{1}{{\sqrt 1 + \sqrt 2 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }} + ... + \frac{1}{{\sqrt k + \sqrt {k + 1} }} = \sqrt {k + 1} - 1\)
Suy ra
\(\begin{array}{l}\frac{1}{{\sqrt 1 + \sqrt 2 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }} + ... + \frac{1}{{\sqrt {k + 1} + \sqrt {k + 2} }}\\ = \sqrt {k + 1} - 1 + \frac{1}{{\sqrt {k + 1} + \sqrt {k + 2} }}\\ = \frac{{{{\left( {\sqrt {k + 1} } \right)}^2} + \sqrt {k + 1} .\sqrt {k + 2} + 1}}{{\sqrt {k + 1} + \sqrt {k + 2} }} - 1\\ = \frac{{k + 2 + \sqrt {k + 1} .\sqrt {k + 2} }}{{\sqrt {k + 1} + \sqrt {k + 2} }} - 1\\ = \frac{{\sqrt {k + 2} \left( {\sqrt {k + 2} + \sqrt {k + 1} } \right)}}{{\sqrt {k + 1} + \sqrt {k + 2} }} - 1\\ = \sqrt {k + 2} - 1\end{array}\)
Vậy đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi \(n \in \mathbb{N}*\). Tức là:
\(\frac{1}{{\sqrt 1 + \sqrt 2 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }} + ... + \frac{1}{{\sqrt n + \sqrt {n + 1} }} = \sqrt {n + 1} - 1\) với mọi \(n \in \mathbb{N}*\)
b) Ta chứng minh bằng quy nạp theo n.
Bước 1: Khi \(n = 2\) ta có \(\frac{{{2^3} - 1}}{{{2^3} + 1}} = \frac{{2({2^2} + 2 + 1)}}{{3.2(2 + 1)}}\), đúng
vì \(\frac{{{2^3} - 1}}{{{2^3} + 1}} = \frac{7}{9};\frac{{2({2^2} + 2 + 1)}}{{3.2(2 + 1)}} = \frac{{2.7}}{{3.2.3}} = \frac{7}{9}\)
Như vậy đẳng thức đúng với \(n = 2\)
Bước 2: Với k là một số nguyên dương lớn hơn 2 tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức đúng với k+1, tức là:
\(\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{{(k + 1)}^3} - 1}}{{{{(k + 1)}^3} + 1}} = \frac{{2({{(k + 1)}^2} + (k + 1) + 1)}}{{3(k + 1)(k + 2)}}\)
Thật vậy, theo giả thiết quy nạp ta có:
\(\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{{(k + 1)}^3} - 1}}{{{{(k + 1)}^3} + 1}} = \frac{{2({{(k + 1)}^2} + (k + 1) + 1)}}{{3(k + 1)(k + 2)}}\)
Suy ra
\(\begin{array}{l}\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{{(k + 1)}^3} - 1}}{{{{(k + 1)}^3} + 1}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{{{(k + 1)}^3} - 1}}{{{{(k + 1)}^3} + 1}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{[(k + 1) - 1][{{(k + 1)}^2} + (k + 1) + 1]}}{{[(k + 1) + 1][{{(k + 1)}^2} - (k + 1) + 1]}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{k[{{(k + 1)}^2} + (k + 1) + 1]}}{{(k + 2)({k^2} + 2k + 1 - k - 1 + 1)}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{k[{{(k + 1)}^2} + (k + 1) + 1]}}{{(k + 2)({k^2} + k + 1)}}\\ = \frac{{2[{{(k + 1)}^2} + (k + 1) + 1]}}{{3(k + 1)(k + 2)}}\end{array}\)
Vậy đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi \(n \in \mathbb{N}*,n \ge 2\). Tức là:
\(\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{n^3} - 1}}{{{n^3} + 1}} = \frac{{2({n^2} + n + 1)}}{{3n(n + 1)}}\) với mọi \(n \in \mathbb{N}*,n \ge 2\)
Chia hình vuông cạnh 1 thành 4 hình vuông nhỏ bằng nhau, lấy ra hình vuông nhỏ thứ nhất (ở góc dưới bên trái, màu đỏ), cạnh của hình vuông đó bằng \(\frac{1}{2}.\)
Chia hình vuông nhỏ ở góc trên bên phải thành bốn hình vuông bằng nhau, lấy ra hình vuông nhỏ thứ hai (màu đỏ), cạnh của hình vuông đó bằng \(\frac{1}{4}.\)
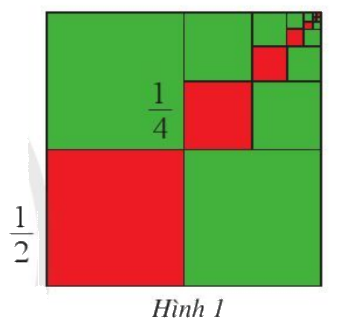
Tiếp tục quá trình trên ta được dãy các hình vuông nhỏ (màu đỏ) ở hình 1.
Cạnh của hình vuông nhỏ thứ n (màu đỏ) bằng bao nhiêu? Vì sao?
Lời giải chi tiết:
Nhận xét:
Chia hình vuông cạnh a thành 4 hình vuông, lấy ra hình vuông nhỏ thứ nhất (như cách lấy ở trên) thì cạnh của hình vuông đó bằng \(\frac{a}{2}\).
=> Sau mỗi lần lấy, độ lớn của cạnh hình vuông giảm đi 2 lần
=> Sau n lần, cạnh hình vuông nhỏ thứ n giảm đi \({2^n}\) so với hình ban đầu.
=> Cạnh của hình vuông nhỏ thứ n là \(\frac{1}{{{2^n}}}\)
Xét mệnh đề chứa biến P(n): “\(1 + 3 + 5 + ... + (2n - 1) = {n^2}\)” với n là số nguyên dương.
a) Chứng tỏ rằng P(1) là mệnh đề đúng.
b) Với k là một số nguyên dương tùy ý mà P(k) là mệnh đề đúng, cho biết \(1 + 3 + 5 + ... + (2k - 1)\) bằng bao nhiêu.
c) Với k là một số nguyên dương tùy ý mà P(k) là mệnh đề đúng, chứng tỏ rằng P(k+1) cũng là mệnh đề đúng bằng cách chỉ ra \({k^2} + [2(k + 1) - 1] = {(k + 1)^2}\).
Lời giải chi tiết:
a) Mệnh đề P(1) là: “\(1 = {1^2}\)”, rõ ràng mệnh đề này đúng.
b) Mệnh đề P(k) là: “\(1 + 3 + 5 + ... + (2k - 1) = {k^2}\)”
Mệnh đề P(k) đúng thì \(1 + 3 + 5 + ... + (2k - 1)\) bằng \({k^2}\)
c) Mệnh đề P(k+1) là: “\(1 + 3 + 5 + ... + [2(k + 1) - 1] = {(k + 1)^2}\)”
Mệnh đề P(k) đúng nên ta có \(1 + 3 + 5 + ... + (2k - 1) = {k^2}\)
\(\begin{array}{l} \Rightarrow 1 + 3 + 5 + ... + [2(k + 1) - 1] = 1 + 3 + 5 + ... + (2k - 1) + [2(k + 1) - 1]\\ = {k^2} + [2(k + 1) - 1] = {k^2} + 2k + 1 = {(k + 1)^2}\end{array}\)
Vậy mệnh đề P(k+1) cũng đúng.
Chứng minh:
a) \(\frac{1}{{\sqrt 1 + \sqrt 2 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }} + ... + \frac{1}{{\sqrt n + \sqrt {n + 1} }} = \sqrt {n + 1} - 1\) với mọi \(n \in \mathbb{N}*\)
b) \(\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{n^3} - 1}}{{{n^3} + 1}} = \frac{{2({n^2} + n + 1)}}{{3n(n + 1)}}\) với mọi \(n \in \mathbb{N}*,n \ge 2\)
Phương pháp giải:
Chứng minh mệnh đề P(n) đúng với \(n \ge p\) thì:
Bước 1: Chứng tỏ mệnh đề đúng với \(n = p\)
Bước 2: Với k là một số nguyên dương tùy ý mà P(k) là mệnh đề đúng, ta chứng tỏ P(k+1) cũng là mệnh đề đúng.
Lời giải chi tiết:
a) Ta chứng minh bằng quy nạp theo n.
Bước 1: Khi \(n = 1\) ta có \(\frac{1}{{\sqrt 1 + \sqrt 2 }} = \sqrt 2 - 1\), đúng
vì \(\left( {\sqrt 2 + \sqrt 1 } \right)\left( {\sqrt 2 - \sqrt 1 } \right) = 2 - 1 = 1 \Rightarrow \frac{1}{{\sqrt 2 + \sqrt 1 }} = \sqrt 2 - \sqrt 1 = \sqrt 2 - 1\)
Như vậy đẳng thức đúng với \(n = 1\)
Bước 2: Với k là một số nguyên dương tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức đúng với k+1, tức là:
\(\frac{1}{{\sqrt 1 + \sqrt 2 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }} + ... + \frac{1}{{\sqrt {k + 1} + \sqrt {k + 2} }} = \sqrt {k + 2} - 1\)
Thật vậy, theo giả thiết quy nạp ta có:
\(\frac{1}{{\sqrt 1 + \sqrt 2 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }} + ... + \frac{1}{{\sqrt k + \sqrt {k + 1} }} = \sqrt {k + 1} - 1\)
Suy ra
\(\begin{array}{l}\frac{1}{{\sqrt 1 + \sqrt 2 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }} + ... + \frac{1}{{\sqrt {k + 1} + \sqrt {k + 2} }}\\ = \sqrt {k + 1} - 1 + \frac{1}{{\sqrt {k + 1} + \sqrt {k + 2} }}\\ = \frac{{{{\left( {\sqrt {k + 1} } \right)}^2} + \sqrt {k + 1} .\sqrt {k + 2} + 1}}{{\sqrt {k + 1} + \sqrt {k + 2} }} - 1\\ = \frac{{k + 2 + \sqrt {k + 1} .\sqrt {k + 2} }}{{\sqrt {k + 1} + \sqrt {k + 2} }} - 1\\ = \frac{{\sqrt {k + 2} \left( {\sqrt {k + 2} + \sqrt {k + 1} } \right)}}{{\sqrt {k + 1} + \sqrt {k + 2} }} - 1\\ = \sqrt {k + 2} - 1\end{array}\)
Vậy đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi \(n \in \mathbb{N}*\). Tức là:
\(\frac{1}{{\sqrt 1 + \sqrt 2 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }} + ... + \frac{1}{{\sqrt n + \sqrt {n + 1} }} = \sqrt {n + 1} - 1\) với mọi \(n \in \mathbb{N}*\)
b) Ta chứng minh bằng quy nạp theo n.
Bước 1: Khi \(n = 2\) ta có \(\frac{{{2^3} - 1}}{{{2^3} + 1}} = \frac{{2({2^2} + 2 + 1)}}{{3.2(2 + 1)}}\), đúng
vì \(\frac{{{2^3} - 1}}{{{2^3} + 1}} = \frac{7}{9};\frac{{2({2^2} + 2 + 1)}}{{3.2(2 + 1)}} = \frac{{2.7}}{{3.2.3}} = \frac{7}{9}\)
Như vậy đẳng thức đúng với \(n = 2\)
Bước 2: Với k là một số nguyên dương lớn hơn 2 tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức đúng với k+1, tức là:
\(\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{{(k + 1)}^3} - 1}}{{{{(k + 1)}^3} + 1}} = \frac{{2({{(k + 1)}^2} + (k + 1) + 1)}}{{3(k + 1)(k + 2)}}\)
Thật vậy, theo giả thiết quy nạp ta có:
\(\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{{(k + 1)}^3} - 1}}{{{{(k + 1)}^3} + 1}} = \frac{{2({{(k + 1)}^2} + (k + 1) + 1)}}{{3(k + 1)(k + 2)}}\)
Suy ra
\(\begin{array}{l}\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{{(k + 1)}^3} - 1}}{{{{(k + 1)}^3} + 1}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{{{(k + 1)}^3} - 1}}{{{{(k + 1)}^3} + 1}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{[(k + 1) - 1][{{(k + 1)}^2} + (k + 1) + 1]}}{{[(k + 1) + 1][{{(k + 1)}^2} - (k + 1) + 1]}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{k[{{(k + 1)}^2} + (k + 1) + 1]}}{{(k + 2)({k^2} + 2k + 1 - k - 1 + 1)}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{k[{{(k + 1)}^2} + (k + 1) + 1]}}{{(k + 2)({k^2} + k + 1)}}\\ = \frac{{2[{{(k + 1)}^2} + (k + 1) + 1]}}{{3(k + 1)(k + 2)}}\end{array}\)
Vậy đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi \(n \in \mathbb{N}*,n \ge 2\). Tức là:
\(\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{n^3} - 1}}{{{n^3} + 1}} = \frac{{2({n^2} + n + 1)}}{{3n(n + 1)}}\) với mọi \(n \in \mathbb{N}*,n \ge 2\)
Chia hình vuông cạnh 1 thành 4 hình vuông nhỏ bằng nhau, lấy ra hình vuông nhỏ thứ nhất (ở góc dưới bên trái, màu đỏ), cạnh của hình vuông đó bằng \(\frac{1}{2}.\)
Chia hình vuông nhỏ ở góc trên bên phải thành bốn hình vuông bằng nhau, lấy ra hình vuông nhỏ thứ hai (màu đỏ), cạnh của hình vuông đó bằng \(\frac{1}{4}.\)
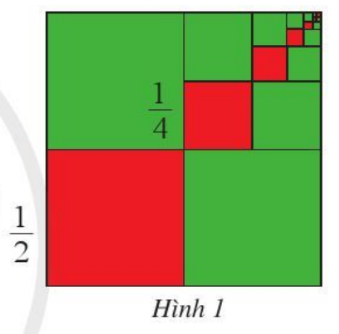
Tiếp tục quá trình trên ta được dãy các hình vuông nhỏ (màu đỏ) ở hình 1.
Cạnh của hình vuông nhỏ thứ n (màu đỏ) bằng bao nhiêu? Vì sao?
Lời giải chi tiết:
Nhận xét:
Chia hình vuông cạnh a thành 4 hình vuông, lấy ra hình vuông nhỏ thứ nhất (như cách lấy ở trên) thì cạnh của hình vuông đó bằng \(\frac{a}{2}\).
=> Sau mỗi lần lấy, độ lớn của cạnh hình vuông giảm đi 2 lần
=> Sau n lần, cạnh hình vuông nhỏ thứ n giảm đi \({2^n}\) so với hình ban đầu.
=> Cạnh của hình vuông nhỏ thứ n là \(\frac{1}{{{2^n}}}\)
Chuyên đề học tập Toán 10 - Cánh diều là một tài liệu quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Mục 1 của chuyên đề này thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng các công thức, định lý đã học để giải quyết các bài toán. Bài viết này sẽ cung cấp lời giải chi tiết cho các bài tập trang 23, 24 và 25, đồng thời phân tích phương pháp giải để giúp bạn hiểu rõ hơn về cách tiếp cận và giải quyết các vấn đề tương tự.
Ở trang 23, các bài tập thường xoay quanh việc xác định các yếu tố của hàm số bậc hai (hệ số a, b, c), tìm đỉnh của parabol, vẽ đồ thị hàm số và xét tính đơn điệu của hàm số. Để giải các bài tập này, bạn cần nắm vững các công thức và định lý liên quan đến hàm số bậc hai, bao gồm:
Ví dụ, bài tập 1 yêu cầu tìm tập xác định của hàm số f(x) = x2 - 4x + 3. Lời giải: Tập xác định của hàm số là R (tập hợp tất cả các số thực) vì hàm số là một đa thức bậc hai.
Trang 24 thường chứa các bài tập về giải bất phương trình bậc hai. Để giải các bài tập này, bạn cần:
Ví dụ, bài tập 2 yêu cầu giải bất phương trình x2 - 5x + 6 > 0. Lời giải: Δ = (-5)2 - 4 * 1 * 6 = 1. Vì Δ > 0, bất phương trình có hai nghiệm phân biệt x1 = 2, x2 = 3. Vậy nghiệm của bất phương trình là x < 2 hoặc x > 3.
Trang 25 thường chứa các bài tập ứng dụng hàm số bậc hai vào giải quyết các bài toán thực tế. Các bài toán này có thể liên quan đến việc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số, hoặc giải các bài toán tối ưu hóa. Để giải các bài tập này, bạn cần:
Ví dụ, bài tập 3 yêu cầu tìm giá trị nhỏ nhất của hàm số f(x) = 2x2 - 8x + 5. Lời giải: x = -(-8)/(2*2) = 2. f(2) = 2*(2)2 - 8*2 + 5 = -3. Vậy giá trị nhỏ nhất của hàm số là -3.
Để học tập và giải toán hiệu quả, bạn nên:
Hy vọng rằng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, bạn sẽ hiểu rõ hơn về cách giải các bài tập trong mục 1 trang 23, 24, 25 Chuyên đề học tập Toán 10 - Cánh diều. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!