Chào mừng các em học sinh đến với lời giải chi tiết Phần A. Tái hiện, củng cố trang 13 Bài tập phát triển năng lực Toán 5 tập 2. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em học sinh ôn tập và củng cố kiến thức một cách hiệu quả.
Chúng tôi hiểu rằng, việc tự giải bài tập đôi khi gặp nhiều khó khăn. Vì vậy, giaitoan.edu.vn sẽ cung cấp đáp án chính xác, kèm theo phương pháp giải rõ ràng, giúp các em hiểu sâu sắc từng bước làm bài.
Tính diện tích xung quanh và diện tích toàn phần của các hình sau ... Hình A có .... hình lập phương nhỏ
Viết số đo thích hợp vào ô trống:
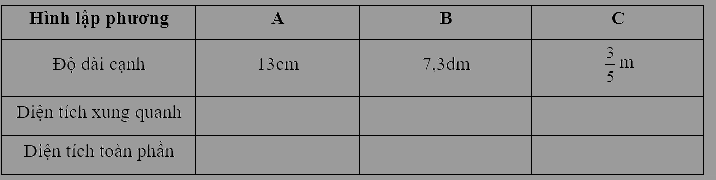
Phương pháp giải:
Áp dụng các công thức:
- Diện tích xung quanh của hình lập phương bằng diện tích một mặt nhân 4
- Diện tích toàn phần của hình lập phương bằng diện tích một mặt nhân 6
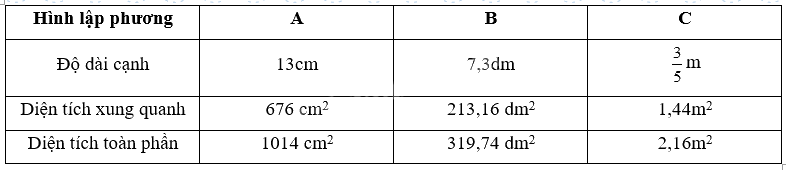
Lời giải chi tiết:
Hình A
Diện tích xung quanh của hình lập phương A là 13 x 13 x 4 = 676 (cm2)
Diện tích toàn phần của hình lập phương A là là 13 x 13 x 6 = 1014 (cm2)
Hình B
Diện tích xung quanh của hình lập phương B là 7,3 x 7,3 x 4 = 213,16 (dm2)
Diện tích toàn phần của hình lập phương B là là 7,3 x 7,3 x 6 = 319,74 (dm2)
Hình C
Diện tích xung quanh của hình lập phương C là $\frac{3}{5} \times \frac{3}{5} \times 4 = \frac{{36}}{{25}} = 1,44$ (m2)
Diện tích toàn phần của hình lập phương C là $\frac{3}{5} \times \frac{3}{5} \times 6 = \frac{{54}}{{25}} = 2,16$ (m2)
Viết số đo thích hợp vào ô trống:
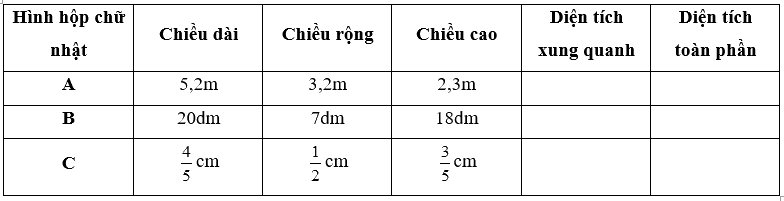
Phương pháp giải:
Áp dụng các công thức:
- Diện tích xung quanh = (chiều dài + chiều rộng) x 2 x chiều cao
- Diện tích toàn phần = diện tích xung quanh + diện tích hai mặt đáy
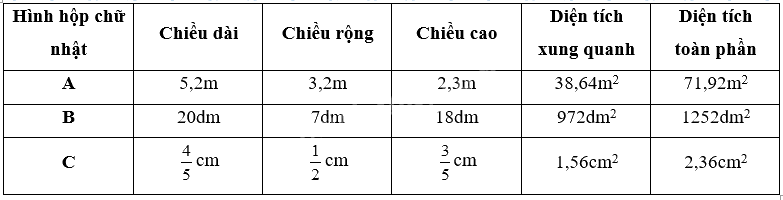
Lời giải chi tiết:
Hình hộp chữ nhật A:
Diện tích xung quanh là (5,2 + 3,2) x 2 x 2,3 = 38,64 (m2)
Diện tích mặt đáy là 5,2 x 3,2 = 16,64 (m2)
Diện tích toàn phần là 38,64 + 16,64 x 2 = 71,92 (m2)
Hình hộp chữ nhật B:
Diện tích xung quanh là (20 + 7) x 2 x 18 = 972 (dm2)
Diện tích mặt đáy là 20 x 7 = 140 (dm2)
Diện tích toàn phần là 972 + 140 x 2 = 1252 (dm2)
Hình hộp chữ nhật C:
Diện tích xung quanh là $\left( {\frac{4}{5} + \frac{1}{2}} \right) \times 2 \times \frac{3}{5} = \frac{{39}}{{25}} = 1,56$ (cm2)
Diện tích mặt đáy là $\frac{4}{5} \times \frac{1}{2} = \frac{2}{5} = 0,4$(cm2)
Diện tích toàn phần là 1,56 + 0,4 x 2 = 2,36 (cm2)
Điền vào chỗ chấm cho thích hợp:
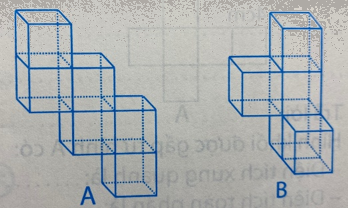
Hình A có .......... hình lập phương nhỏ.
Hình B có .......... hình lập phương nhỏ.
Hình................... có thể tích lớn hơn thể tích hình........................
Phương pháp giải:
Đếm số hình lập phương nhỏ của mỗi hình.
Hình nào có nhiều hình lập phương nhỏ hơn thì có thể tích lớn hơn.
Lời giải chi tiết:
Hình A có 6 hình lập phương nhỏ.
Hình B có 5 hình lập phương nhỏ.
Hình A có thể tích lớn hơn thể tích hình B
Viết số đo thích hợp vào chỗ chấm:
Tính diện tích xung quanh và diện tích toàn phần của các hình sau:

Phương pháp giải:
Áp dụng các công thức:
- Diện tích xung quanh của hình lập phương bằng diện tích một mặt nhân 4
- Diện tích toàn phần của hình lập phương bằng diện tích một mặt nhân 6
- Diện tích một mặt bằng cạnh nhân cạnh
Lời giải chi tiết:
Hình lập phương có cạnh 4 cm:
Diện tích xung quanh là: 4 x 4 x 4 = 64 (cm2)
Diện tích toàn phần là: 4 x 4 x 6 = 96 (cm2)
Hình lập phương có cạnh 13 cm:
Diện tích xung quang là: 13 x 13 x 4 = 676 (cm2)
Diện tích toàn phần là: 13 x 13 x 6 = 1014 (cm2)
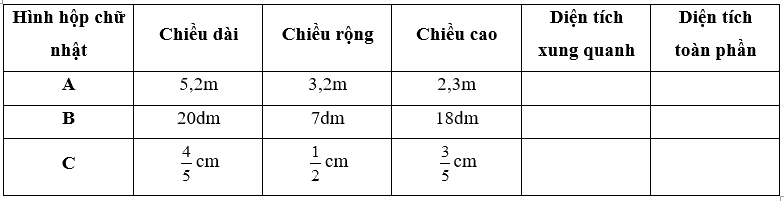
Viết số đo thích hợp vào ô trống:
Phương pháp giải:
Áp dụng các công thức:
- Diện tích xung quanh = (chiều dài + chiều rộng) x 2 x chiều cao
- Diện tích toàn phần = diện tích xung quanh + diện tích hai mặt đáy
Lời giải chi tiết:
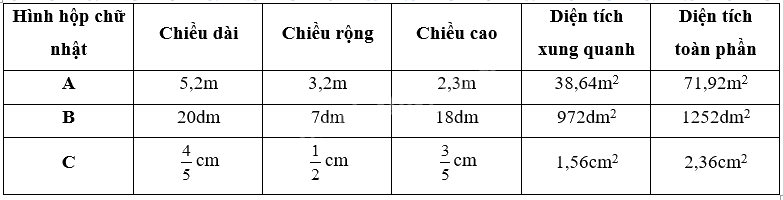
Hình hộp chữ nhật A:
Diện tích xung quanh là (5,2 + 3,2) x 2 x 2,3 = 38,64 (m2)
Diện tích mặt đáy là 5,2 x 3,2 = 16,64 (m2)
Diện tích toàn phần là 38,64 + 16,64 x 2 = 71,92 (m2)
Hình hộp chữ nhật B:
Diện tích xung quanh là (20 + 7) x 2 x 18 = 972 (dm2)
Diện tích mặt đáy là 20 x 7 = 140 (dm2)
Diện tích toàn phần là 972 + 140 x 2 = 1252 (dm2)
Hình hộp chữ nhật C:
Diện tích xung quanh là $\left( {\frac{4}{5} + \frac{1}{2}} \right) \times 2 \times \frac{3}{5} = \frac{{39}}{{25}} = 1,56$ (cm2)
Diện tích mặt đáy là $\frac{4}{5} \times \frac{1}{2} = \frac{2}{5} = 0,4$(cm2)
Diện tích toàn phần là 1,56 + 0,4 x 2 = 2,36 (cm2)
Viết số đo thích hợp vào ô trống:
Phương pháp giải:
Áp dụng các công thức:
- Diện tích xung quanh của hình lập phương bằng diện tích một mặt nhân 4
- Diện tích toàn phần của hình lập phương bằng diện tích một mặt nhân 6
Lời giải chi tiết:
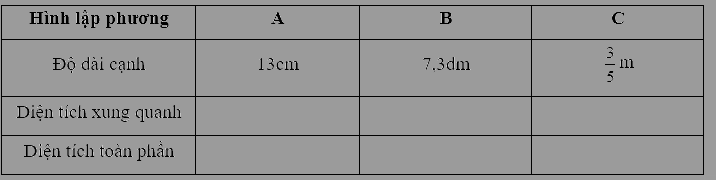
Hình A
Diện tích xung quanh của hình lập phương A là 13 x 13 x 4 = 676 (cm2)
Diện tích toàn phần của hình lập phương A là là 13 x 13 x 6 = 1014 (cm2)
Hình B
Diện tích xung quanh của hình lập phương B là 7,3 x 7,3 x 4 = 213,16 (dm2)
Diện tích toàn phần của hình lập phương B là là 7,3 x 7,3 x 6 = 319,74 (dm2)
Hình C
Diện tích xung quanh của hình lập phương C là $\frac{3}{5} \times \frac{3}{5} \times 4 = \frac{{36}}{{25}} = 1,44$ (m2)
Diện tích toàn phần của hình lập phương C là $\frac{3}{5} \times \frac{3}{5} \times 6 = \frac{{54}}{{25}} = 2,16$ (m2)
Viết số đo thích hợp vào chỗ chấm:
Tính diện tích xung quanh và diện tích toàn phần của các hình sau:

Phương pháp giải:
Áp dụng các công thức:
- Diện tích xung quanh của hình lập phương bằng diện tích một mặt nhân 4
- Diện tích toàn phần của hình lập phương bằng diện tích một mặt nhân 6
- Diện tích một mặt bằng cạnh nhân cạnh
Lời giải chi tiết:
Hình lập phương có cạnh 4 cm:
Diện tích xung quanh là: 4 x 4 x 4 = 64 (cm2)
Diện tích toàn phần là: 4 x 4 x 6 = 96 (cm2)
Hình lập phương có cạnh 13 cm:
Diện tích xung quang là: 13 x 13 x 4 = 676 (cm2)
Diện tích toàn phần là: 13 x 13 x 6 = 1014 (cm2)
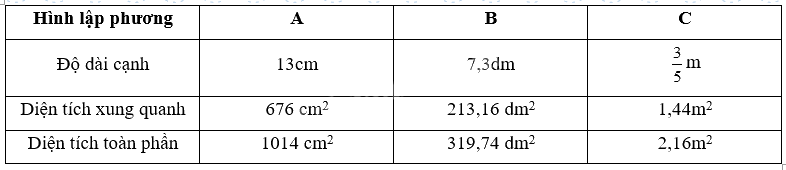
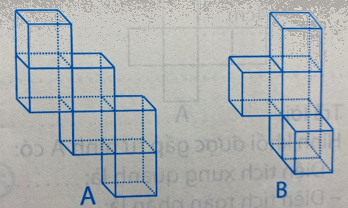
Điền vào chỗ chấm cho thích hợp:
Hình A có .......... hình lập phương nhỏ.
Hình B có .......... hình lập phương nhỏ.
Hình................... có thể tích lớn hơn thể tích hình........................
Phương pháp giải:
Đếm số hình lập phương nhỏ của mỗi hình.
Hình nào có nhiều hình lập phương nhỏ hơn thì có thể tích lớn hơn.
Lời giải chi tiết:
Hình A có 6 hình lập phương nhỏ.
Hình B có 5 hình lập phương nhỏ.
Hình A có thể tích lớn hơn thể tích hình B
Phần A. Tái hiện, củng cố trang 13 trong Bài tập phát triển năng lực Toán 5 tập 2 tập trung vào việc giúp học sinh ôn lại các kiến thức đã học và vận dụng vào giải quyết các bài toán thực tế. Các bài tập trong phần này thường mang tính ứng dụng cao, đòi hỏi học sinh phải hiểu rõ bản chất của vấn đề và có khả năng tư duy logic.
Phần A bao gồm các bài tập liên quan đến các chủ đề sau:
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong Phần A:
Bài tập này yêu cầu học sinh tính nhẩm nhanh các phép tính đơn giản với số thập phân. Để làm bài này, học sinh cần nắm vững các quy tắc về phép cộng, trừ, nhân, chia số thập phân.
Ví dụ: 2,5 + 3,7 = ?
Cách giải: Cộng phần nguyên và phần thập phân riêng biệt, sau đó ghép lại. 2 + 3 = 5; 0,5 + 0,7 = 1,2. Vậy 2,5 + 3,7 = 6,2
Bài tập này yêu cầu học sinh giải các bài toán có liên quan đến thực tế, áp dụng các kiến thức đã học về số thập phân, phép tính, diện tích, thể tích.
Ví dụ: Một mảnh đất hình chữ nhật có chiều dài 12,5m, chiều rộng 8m. Tính diện tích mảnh đất đó.
Cách giải: Diện tích hình chữ nhật = chiều dài x chiều rộng. Vậy diện tích mảnh đất là: 12,5 x 8 = 100 (m2)
Để học tốt môn Toán 5, các em học sinh cần:
Việc giải các bài tập phát triển năng lực không chỉ giúp học sinh củng cố kiến thức mà còn giúp các em phát triển các kỹ năng quan trọng như:
Hy vọng rằng, với hướng dẫn chi tiết và các mẹo học tập hiệu quả trên, các em học sinh sẽ tự tin hơn khi giải Phần A. Tái hiện, củng cố trang 13 Bài tập phát triển năng lực Toán 5 tập 2. Chúc các em học tập tốt!
| Chủ đề | Mục tiêu |
|---|---|
| Số thập phân | Nắm vững các phép tính và quy tắc chuyển đổi. |
| Diện tích | Tính toán diện tích các hình cơ bản. |
| Thể tích | Tính toán thể tích hình hộp chữ nhật. |