Chào mừng các em học sinh đến với bài giải chi tiết Giải phần B. Kết nối trang 33 Bài tập phát triển năng lực Toán 5. Tại giaitoan.edu.vn, chúng tôi luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Bài tập này thuộc chương trình Toán 5 Kết nối, nhằm giúp các em rèn luyện kỹ năng giải toán và vận dụng kiến thức đã học vào thực tế.
Điền dấu >, <, = thích hợp vào chỗ chấm: Tìm số tự nhiên x thỏa mãn:
Tìm số tự nhiên x thỏa mãn:
a) 1,23 < x < 2,13
b) 47,8 > x > 45,6
c) 164,32 < x < 169,9
Phương pháp giải:
Tìm số tự nhiên thỏa mãn yêu cầu của đề bài.
Lời giải chi tiết:
a) 1,23 < x < 2,13
Vậy x = 2
b) 47,8 > x > 45,6
Vậy x = 46 hoặc x = 47
c) 164,32 < x < 169,9
Vậy x = 165 ; 166 ; 167 ; 168 hoặc 169
Tìm số thập phân có một chữ số ở phần thập phân thỏa mãn:
a) 34,12 < x < 34,56
b) 9,86 < x < 9,45
c) 12 < x < 13
Phương pháp giải:
Áp dụng quy tắc so sánh hai số thập phân:
+ So sánh các phần nguyên của hai số đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.
+ Nếu phần nguyên của hai số đó bằng nhau thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn ...
Lời giải chi tiết:
a) 34,12 < x < 34,56
Vậy x = 34,2 ; 34,3 ; 34,4 hoặc 34,5
b) 9,86 > x > 9,45
Vậy x = 9,8 ; 9,7 ; 9,6 hoặc 9,5
c) 12 < x < 13
Vậy x = 12,1 ; 12,2 ; 12,3 ; 12,4 ; 12,5 ; 12,6 ; 12,7 ; 12,8 ; 12,9
Tìm hai số tự nhiên x, y liên tiếp sao cho:
a) x < 20,3 < y
b) x < 16,78 < y
Phương pháp giải:
Dựa vào cách so sánh số thập phân để tìm giá trị thích hợp của x, y.
Lời giải chi tiết:
a) x < 20,3 < y
Ta có 20 < 20,3 < 21
Vậy x = 20, y = 21
b) x < 16,78 < y
Ta có 16 < 16,78 < 17
Vậy x = 16, y = 17
Tính bằng cách thuận tiện:
a) $\frac{{84 \times 36}}{{18 \times 252}}$
b) $\frac{{13 \times 125 \times 16}}{{8 \times 52 \times 25}}$
Phương pháp giải:
Tách tích ở tử số thành tích của các thừa số, sau đó lần lượt chia tử số và mẫu số cho các thừa số chung.
Lời giải chi tiết:
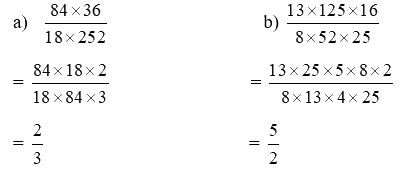
Viết chữ số thích hợp vào chỗ chấm:
34,….67 < 34,167 231,45 = 231,4…..
12…,321 < 121,321 26,3…6 > 26,386
345,4…5 = 345,…25 461,2…4 < 461,214
Phương pháp giải:
Nếu phần nguyên của hai số đó bằng nhau thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn ... đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.
Lời giải chi tiết:
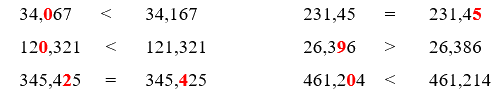
Điền dấu >, <, = thích hợp vào chỗ chấm:

Phương pháp giải:
So sánh các số thập phân rồi điền dấu thích hợp vào chỗ chấm.
Lời giải chi tiết:

Điền dấu >, <, = thích hợp vào chỗ chấm:

Phương pháp giải:
So sánh các số thập phân rồi điền dấu thích hợp vào chỗ chấm.
Lời giải chi tiết:

Viết chữ số thích hợp vào chỗ chấm:
34,….67 < 34,167 231,45 = 231,4…..
12…,321 < 121,321 26,3…6 > 26,386
345,4…5 = 345,…25 461,2…4 < 461,214
Phương pháp giải:
Nếu phần nguyên của hai số đó bằng nhau thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn ... đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.
Lời giải chi tiết:
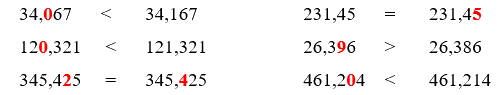
Tìm số tự nhiên x thỏa mãn:
a) 1,23 < x < 2,13
b) 47,8 > x > 45,6
c) 164,32 < x < 169,9
Phương pháp giải:
Tìm số tự nhiên thỏa mãn yêu cầu của đề bài.
Lời giải chi tiết:
a) 1,23 < x < 2,13
Vậy x = 2
b) 47,8 > x > 45,6
Vậy x = 46 hoặc x = 47
c) 164,32 < x < 169,9
Vậy x = 165 ; 166 ; 167 ; 168 hoặc 169
Tìm số thập phân có một chữ số ở phần thập phân thỏa mãn:
a) 34,12 < x < 34,56
b) 9,86 < x < 9,45
c) 12 < x < 13
Phương pháp giải:
Áp dụng quy tắc so sánh hai số thập phân:
+ So sánh các phần nguyên của hai số đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.
+ Nếu phần nguyên của hai số đó bằng nhau thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn ...
Lời giải chi tiết:
a) 34,12 < x < 34,56
Vậy x = 34,2 ; 34,3 ; 34,4 hoặc 34,5
b) 9,86 > x > 9,45
Vậy x = 9,8 ; 9,7 ; 9,6 hoặc 9,5
c) 12 < x < 13
Vậy x = 12,1 ; 12,2 ; 12,3 ; 12,4 ; 12,5 ; 12,6 ; 12,7 ; 12,8 ; 12,9
Tìm hai số tự nhiên x, y liên tiếp sao cho:
a) x < 20,3 < y
b) x < 16,78 < y
Phương pháp giải:
Dựa vào cách so sánh số thập phân để tìm giá trị thích hợp của x, y.
Lời giải chi tiết:
a) x < 20,3 < y
Ta có 20 < 20,3 < 21
Vậy x = 20, y = 21
b) x < 16,78 < y
Ta có 16 < 16,78 < 17
Vậy x = 16, y = 17
Tính bằng cách thuận tiện:
a) $\frac{{84 \times 36}}{{18 \times 252}}$
b) $\frac{{13 \times 125 \times 16}}{{8 \times 52 \times 25}}$
Phương pháp giải:
Tách tích ở tử số thành tích của các thừa số, sau đó lần lượt chia tử số và mẫu số cho các thừa số chung.
Lời giải chi tiết:
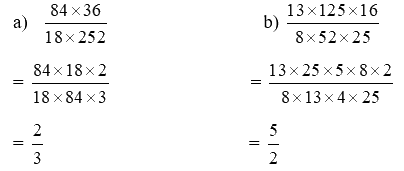
Bài tập phần B trang 33 Toán 5 Kết nối tập trung vào việc củng cố kiến thức về các phép tính với phân số, đặc biệt là các bài toán liên quan đến tìm phân số theo tỉ lệ. Các bài toán này đòi hỏi học sinh phải nắm vững các khái niệm cơ bản về phân số, tỉ số và khả năng vận dụng linh hoạt các công thức để giải quyết vấn đề.
Bài tập phần B bao gồm các dạng toán sau:
Đề bài: Hai phân số có tổng bằng 5/6 và tỉ số là 2/3. Tìm hai phân số đó.
Giải:
Đề bài: Hai phân số có hiệu bằng 1/4 và tỉ số là 1/2. Tìm hai phân số đó.
Giải:
(Tương tự như bài 1, hướng dẫn giải chi tiết các bước)
Đề bài: Một cửa hàng có một số gạo. Sau khi bán đi 2/5 số gạo, còn lại 30kg. Hỏi lúc đầu cửa hàng có bao nhiêu kg gạo?
Giải:
Để giải nhanh các bài toán tìm phân số theo tỉ lệ, học sinh có thể sử dụng phương pháp tổng tỉ hoặc hiệu tỉ. Điều quan trọng là phải xác định đúng tổng hoặc hiệu của hai phân số và tỉ số giữa chúng.
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, học sinh có thể tự giải thêm các bài tập tương tự trong sách giáo khoa hoặc các tài liệu tham khảo khác.
Hy vọng với bài giải chi tiết này, các em học sinh đã hiểu rõ cách giải các bài tập phần B trang 33 Bài tập phát triển năng lực Toán 5 Kết nối. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!