Chào mừng các em học sinh đến với bài giải chi tiết Giải phần B. Kết nối trang 74 Toán 5. Bài viết này thuộc bộ tài liệu hướng dẫn giải bài tập Toán 5 Kết nối, được cung cấp bởi giaitoan.edu.vn. Chúng tôi luôn cố gắng cung cấp những lời giải dễ hiểu, chính xác nhất để giúp các em học tập tốt hơn.
Viết số thập phân thích hợp vào chỗ chấm: 19m 5dm = m Viết tiếp vào chỗ chấm rồi tính diện tích các hình tam giác vuông sau: a) Tam giác vuông ABC có: - Độ dài đáy là:
Tính bằng cách hợp lí:
a) 3,5 x 4,2 + 3,6 x 3,5 + 3,5 x 2,2
b) 12,6 x 5,05 – 6,3 x 4,7 – 6,3 x 5,3
c)4,5 x 92,5 – 18 x 2,5 + 4,5 x 17,5
Phương pháp giải:
Áp dụng các công thức:
(a + b) x c = a x c + b x c
(a - b) x c = a x c - b x c
Lời giải chi tiết:
a) 3,5 x 4,2 + 3,6 x 3,5 + 3,5 x 2,2
= 3,5 x (4,2 + 3,6 + 2,2)
= 3,5 x 10
= 35
b) 12,6 x 5,05 – 6,3 x 4,7 – 6,3 x 5,3
= 2 x 6,3 x 5,05 – 6,3 x 4,7 – 6,3 x 5,3
= 6,3 x (2 x 5,05 – 4,7 – 5,3)
= 6,3 x 0,1
= 0,63
c) 4,5 x 92,5 – 18 x 2,5 + 4,5 x 17,5
= 4,5 x 92,5 – 4 x 4,5 x 2,5 + 4,5 x 17,5
= 4,5 x (92,5 – 4 x 2,5 + 17,5)
= 4,5 x 100
= 450
Một hình tam giác có độ dài đáy là 5dm và chiều cao gấp đôi cạnh đáy. Tính diện tích hình tam giác đó.
Phương pháp giải:
Bước 1: Chiều cao của hình tam giác = độ dài cạnh đáy x 2
Bước 2: Muốn tính diện tích của hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
Lời giải chi tiết:
Chiều cao của tam giác là:
5 x 2 = 10 (dm)
Diện tích hình tam giác đó là:
$\frac{{5 \times 10}}{2} = 25$ (dm2)
Đáp số: 25 dm2
Nếu tăng cạnh một hình vuông thêm 25% thì ta được hình vuông mới có chu vi 25cm. Tính chu vi của hình vuông lúc đầu.
Phương pháp giải:
- Tính độ dài cạnh hình vuông mới
- Cạnh của hình vuông mới bằng 125% độ dài cạnh hình vuông ban đầu.
- Tìm độ dài cạnh của hình vuông ban đầu
- Tính chu vi của hình vuông lúc đầu
Lời giải chi tiết:
Cạnh của hình vuông mới là
25 : 4 = 6,25 (cm)
Cạnh của hình vuông mới bằng 125% độ dài cạnh hình vuông ban đầu.
Cạnh hình vuông ban đầu là
6,25 : 125 x 100 = 5 (cm)
Chu vi của hình vuông lúc đầu là
5 x 4 = 20 (cm)
Đáp số: 20 cm
Viết số thập phân thích hợp vào chỗ chấm:
19m 5dm = ………… m
35m 8cm = …………. m
17km 8hm = ………… km
28hm 5m = …………… hm
7m2 5dm2 = …………… m2
8 hm2 9dam2 = .......................... hm2
6dm2 15cm2 = ........................... dm2
9m2 12dm2 = ............................. m2
Phương pháp giải:
Xác định mối liên hệ giữa các đơn vị đo độ dài để viết các số đo dưới dạng hỗn số thích hợp, sau đó viết dưới dạng số thập phân.
Lời giải chi tiết:

Viết tiếp vào chỗ chấm rồi tính diện tích các hình tam giác vuông sau:
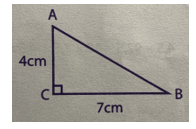
a) Tam giác vuông ABC có:
- Độ dài đáy là: ........................................................
- Chiều cao tương ứng là .........................................
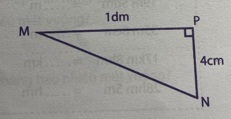
b) Tam giác vuông MNP có:
- Độ dài đáy là: ........................................................
- Chiều cao tương ứng là ...........................................
Phương pháp giải:
- Quan sát hình vẽ để điền thông tin còn thiếu vào chỗ trống.
- Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
Lời giải chi tiết:
a) Tam giác vuông ABC có:
- Độ dài đáy là BC = 7cm
- Chiều cao tương ứng là AC = 4cm
Diện tích tam giác vuông ABC là:
$\frac{{7 \times 4}}{2} = 14$ (cm2)
Đáp số: 14cm2
b) Tam giác vuông MNP có:
- Độ dài đáy là: MP = 1dm = 10 cm
- Chiều cao tương ứng là PN = 4cm
Diện tích tam giác vuông MNP là:
$\frac{{10 \times 4}}{2} = 20$= 2 (cm2)
Đáp số: 2 cm2
Viết tiếp vào chỗ chấm rồi tính diện tích các hình tam giác vuông sau:
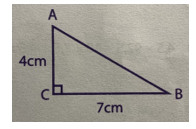
a) Tam giác vuông ABC có:
- Độ dài đáy là: ........................................................
- Chiều cao tương ứng là .........................................
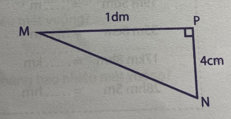
b) Tam giác vuông MNP có:
- Độ dài đáy là: ........................................................
- Chiều cao tương ứng là ...........................................
Phương pháp giải:
- Quan sát hình vẽ để điền thông tin còn thiếu vào chỗ trống.
- Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
Lời giải chi tiết:
a) Tam giác vuông ABC có:
- Độ dài đáy là BC = 7cm
- Chiều cao tương ứng là AC = 4cm
Diện tích tam giác vuông ABC là:
$\frac{{7 \times 4}}{2} = 14$ (cm2)
Đáp số: 14cm2
b) Tam giác vuông MNP có:
- Độ dài đáy là: MP = 1dm = 10 cm
- Chiều cao tương ứng là PN = 4cm
Diện tích tam giác vuông MNP là:
$\frac{{10 \times 4}}{2} = 20$= 2 (cm2)
Đáp số: 2 cm2
Tính bằng cách hợp lí:
a) 3,5 x 4,2 + 3,6 x 3,5 + 3,5 x 2,2
b) 12,6 x 5,05 – 6,3 x 4,7 – 6,3 x 5,3
c)4,5 x 92,5 – 18 x 2,5 + 4,5 x 17,5
Phương pháp giải:
Áp dụng các công thức:
(a + b) x c = a x c + b x c
(a - b) x c = a x c - b x c
Lời giải chi tiết:
a) 3,5 x 4,2 + 3,6 x 3,5 + 3,5 x 2,2
= 3,5 x (4,2 + 3,6 + 2,2)
= 3,5 x 10
= 35
b) 12,6 x 5,05 – 6,3 x 4,7 – 6,3 x 5,3
= 2 x 6,3 x 5,05 – 6,3 x 4,7 – 6,3 x 5,3
= 6,3 x (2 x 5,05 – 4,7 – 5,3)
= 6,3 x 0,1
= 0,63
c) 4,5 x 92,5 – 18 x 2,5 + 4,5 x 17,5
= 4,5 x 92,5 – 4 x 4,5 x 2,5 + 4,5 x 17,5
= 4,5 x (92,5 – 4 x 2,5 + 17,5)
= 4,5 x 100
= 450
Viết số thập phân thích hợp vào chỗ chấm:
19m 5dm = ………… m
35m 8cm = …………. m
17km 8hm = ………… km
28hm 5m = …………… hm
7m2 5dm2 = …………… m2
8 hm2 9dam2 = .......................... hm2
6dm2 15cm2 = ........................... dm2
9m2 12dm2 = ............................. m2
Phương pháp giải:
Xác định mối liên hệ giữa các đơn vị đo độ dài để viết các số đo dưới dạng hỗn số thích hợp, sau đó viết dưới dạng số thập phân.
Lời giải chi tiết:

Một hình tam giác có độ dài đáy là 5dm và chiều cao gấp đôi cạnh đáy. Tính diện tích hình tam giác đó.
Phương pháp giải:
Bước 1: Chiều cao của hình tam giác = độ dài cạnh đáy x 2
Bước 2: Muốn tính diện tích của hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
Lời giải chi tiết:
Chiều cao của tam giác là:
5 x 2 = 10 (dm)
Diện tích hình tam giác đó là:
$\frac{{5 \times 10}}{2} = 25$ (dm2)
Đáp số: 25 dm2
Nếu tăng cạnh một hình vuông thêm 25% thì ta được hình vuông mới có chu vi 25cm. Tính chu vi của hình vuông lúc đầu.
Phương pháp giải:
- Tính độ dài cạnh hình vuông mới
- Cạnh của hình vuông mới bằng 125% độ dài cạnh hình vuông ban đầu.
- Tìm độ dài cạnh của hình vuông ban đầu
- Tính chu vi của hình vuông lúc đầu
Lời giải chi tiết:
Cạnh của hình vuông mới là
25 : 4 = 6,25 (cm)
Cạnh của hình vuông mới bằng 125% độ dài cạnh hình vuông ban đầu.
Cạnh hình vuông ban đầu là
6,25 : 125 x 100 = 5 (cm)
Chu vi của hình vuông lúc đầu là
5 x 4 = 20 (cm)
Đáp số: 20 cm
Bài tập phần B trang 74 Toán 5 Kết nối là một phần quan trọng trong chương trình học, giúp học sinh rèn luyện kỹ năng giải quyết các bài toán thực tế liên quan đến các phép tính với số thập phân. Bài tập này tập trung vào việc vận dụng kiến thức đã học để giải các bài toán có tính ứng dụng cao, giúp học sinh hiểu rõ hơn về mối liên hệ giữa toán học và cuộc sống.
Phần B trang 74 bao gồm các bài tập sau:
Để giải bài tập này, học sinh cần nắm vững công thức tính diện tích hình chữ nhật (chiều dài x chiều rộng) và hình vuông (cạnh x cạnh). Các em cần đọc kỹ đề bài để xác định đúng chiều dài, chiều rộng hoặc cạnh của hình, sau đó áp dụng công thức để tính diện tích.
Ví dụ: Một hình chữ nhật có chiều dài 5cm và chiều rộng 3cm. Diện tích của hình chữ nhật là: 5cm x 3cm = 15cm2
Để giải bài tập này, học sinh cần nắm vững công thức tính chu vi hình chữ nhật (2 x (chiều dài + chiều rộng)) và hình vuông (4 x cạnh). Tương tự như bài tập 1, các em cần đọc kỹ đề bài để xác định đúng chiều dài, chiều rộng hoặc cạnh của hình, sau đó áp dụng công thức để tính chu vi.
Ví dụ: Một hình vuông có cạnh 4cm. Chu vi của hình vuông là: 4cm x 4 = 16cm
Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép tính với số thập phân để tính tổng số tiền phải trả khi mua nhiều sản phẩm với các mức giá khác nhau. Các em cần chú ý đến đơn vị tiền tệ và thực hiện các phép tính cộng, trừ, nhân, chia một cách chính xác.
Ví dụ: An mua 2 bút bi giá 3000 đồng/cái và 1 quyển vở giá 5000 đồng. Tổng số tiền An phải trả là: (2 x 3000) + 5000 = 11000 đồng
Bài tập này yêu cầu học sinh vận dụng kiến thức về mối quan hệ giữa quãng đường, vận tốc và thời gian (quãng đường = vận tốc x thời gian). Các em cần xác định đúng quãng đường và vận tốc, sau đó sử dụng công thức để tính thời gian đi đường.
Ví dụ: Một ô tô đi từ A đến B với vận tốc 60km/giờ và quãng đường là 180km. Thời gian ô tô đi từ A đến B là: 180km / 60km/giờ = 3 giờ
Việc luyện tập thường xuyên là yếu tố quan trọng để học sinh nắm vững kiến thức và kỹ năng giải toán. Các em nên dành thời gian làm thêm các bài tập tương tự để rèn luyện khả năng giải quyết vấn đề và tự tin hơn trong các kỳ thi.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi giải Giải phần B. Kết nối trang 74 Bài tập phát triển năng lực Toán 5. Chúc các em học tập tốt và đạt kết quả cao!