Chào mừng các em học sinh lớp 5 đến với bài giải chi tiết phần A. Tái hiện, củng cố trang 44 trong sách Bài tập phát triển năng lực Toán 5. Bài viết này sẽ giúp các em hiểu rõ phương pháp giải và tự tin làm bài tập.
Giaitoan.edu.vn cung cấp lời giải chính xác, dễ hiểu, cùng với các bài giảng video hướng dẫn chi tiết, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Sử dụng tính chất giao hoán và tính chất kết hợp để tính: a) 38,5 + 47,6 + 31,5 + 24,4. Đặt tính rồi tính: 2,14 x 6
Sử dụng tính chất giao hoán và tính chất kết hợp để tính:
a) 38,5 + 47,6 + 31,5 + 24,4
b) 132,17 + 234,45 + 158,83 + 72,55
c) 43,8 + 135,34 + 27,2 + 253,66
Phương pháp giải:
Sử dụng tính chất giao hoán và tính chất kết hợp để ghép các số có tổng là số tự nhiên.
Lời giải chi tiết:
a) 38,5 + 47,6 + 31,5 + 24,4 = (38,5 + 31,5) + (47,6 + 24,4)
= 70 + 72 = 142
b) 132,17 + 234,45 + 158,83 + 72,55 = (132,17 + 158,83) + (234,45 + 72,55)
= 291 + 307 = 598
c) 43,8 + 135,34 + 27,2 + 253,66 = (43,8 + 27,2) + (135,34 + 253,66)
= 71 + 389 = 460
Một ô tô trong 3 giờ đi được 163km. Giờ thứ nhất đi được 35,4km, giờ thứ hai đi được số ki-lô-mét gấp đôi giờ thứ nhất. Hỏi giờ thứ ba ô tô đó đi được bao nhiêu ki-lô-mét?
Phương pháp giải:
- Tìm số km đi trong giờ thứ hai = Số km đi trong giờ thứ nhất x 2
- Tìm số km đi trong giờ thứ ba = Số km đi trong 3 giờ - (Số km đi trong giờ thứ nhất + Số km đi trong giờ thứ hai)
Lời giải chi tiết:
Giờ thứ hai đi được số ki-lô-mét là:
35,4 x 2 = 70,8 (km)
Giờ thứ ba ô tô đó đi được số ki-lô-mét là:
163 – 35,4 – 70,8 = 56,8 (km)
Đáp số: 56,8km
Viết số thích hợp vào ô trống:

Phương pháp giải:
Áp dụng các công thức:
Hiệu = số bị trừ - số trừ
Số trừ = số bị trừ - hiệu
Số bị trừ = hiệu + số trừ
Lời giải chi tiết:

Đặt tính rồi tính:
2,14 x 6
1,037 x 4
31,2 x 21
Phương pháp giải:
- Nhân như nhân các số tự nhiên
- Đếm xem trong phần thập phân của số thập phân có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.
Lời giải chi tiết:
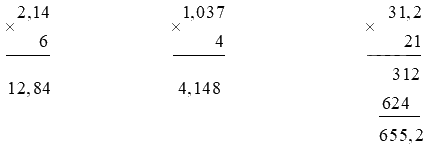
Đặt tính rồi tính:
125,4 – 32,7
655,32 – 217,09
453,312 – 217,16
Phương pháp giải:
- Viết số trừ dưới số bị trừ sao cho các chữ số ở cùng một hàng đặt thẳng cột nhau.
- Thực hiện phép trừ như trừ các số tự nhiên.
- Viết dấu phẩy ở hiệu thẳng cột với các dấu phẩy của số bị trừ và số trừ.
Lời giải chi tiết:
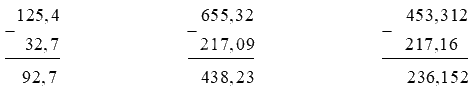
Sử dụng tính chất giao hoán và tính chất kết hợp để tính:
a) 38,5 + 47,6 + 31,5 + 24,4
b) 132,17 + 234,45 + 158,83 + 72,55
c) 43,8 + 135,34 + 27,2 + 253,66
Phương pháp giải:
Sử dụng tính chất giao hoán và tính chất kết hợp để ghép các số có tổng là số tự nhiên.
Lời giải chi tiết:
a) 38,5 + 47,6 + 31,5 + 24,4 = (38,5 + 31,5) + (47,6 + 24,4)
= 70 + 72 = 142
b) 132,17 + 234,45 + 158,83 + 72,55 = (132,17 + 158,83) + (234,45 + 72,55)
= 291 + 307 = 598
c) 43,8 + 135,34 + 27,2 + 253,66 = (43,8 + 27,2) + (135,34 + 253,66)
= 71 + 389 = 460
Viết số thích hợp vào ô trống:

Phương pháp giải:
Áp dụng các công thức:
Hiệu = số bị trừ - số trừ
Số trừ = số bị trừ - hiệu
Số bị trừ = hiệu + số trừ
Lời giải chi tiết:

Đặt tính rồi tính:
125,4 – 32,7
655,32 – 217,09
453,312 – 217,16
Phương pháp giải:
- Viết số trừ dưới số bị trừ sao cho các chữ số ở cùng một hàng đặt thẳng cột nhau.
- Thực hiện phép trừ như trừ các số tự nhiên.
- Viết dấu phẩy ở hiệu thẳng cột với các dấu phẩy của số bị trừ và số trừ.
Lời giải chi tiết:
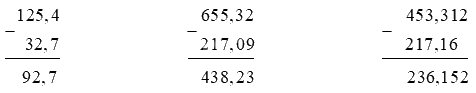
Đặt tính rồi tính:
2,14 x 6
1,037 x 4
31,2 x 21
Phương pháp giải:
- Nhân như nhân các số tự nhiên
- Đếm xem trong phần thập phân của số thập phân có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.
Lời giải chi tiết:
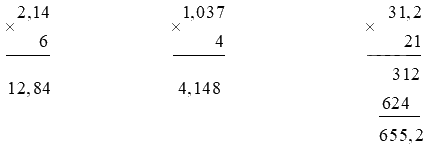
Một ô tô trong 3 giờ đi được 163km. Giờ thứ nhất đi được 35,4km, giờ thứ hai đi được số ki-lô-mét gấp đôi giờ thứ nhất. Hỏi giờ thứ ba ô tô đó đi được bao nhiêu ki-lô-mét?
Phương pháp giải:
- Tìm số km đi trong giờ thứ hai = Số km đi trong giờ thứ nhất x 2
- Tìm số km đi trong giờ thứ ba = Số km đi trong 3 giờ - (Số km đi trong giờ thứ nhất + Số km đi trong giờ thứ hai)
Lời giải chi tiết:
Giờ thứ hai đi được số ki-lô-mét là:
35,4 x 2 = 70,8 (km)
Giờ thứ ba ô tô đó đi được số ki-lô-mét là:
163 – 35,4 – 70,8 = 56,8 (km)
Đáp số: 56,8km
Phần A. Tái hiện, củng cố trang 44 trong Bài tập phát triển năng lực Toán 5 tập trung vào việc ôn lại các kiến thức đã học về các phép tính với số thập phân, các bài toán liên quan đến đo lường thời gian, quãng đường và vận tốc. Mục tiêu của phần này là giúp học sinh củng cố kiến thức nền tảng và rèn luyện kỹ năng giải toán thực tế.
Bài 1 yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia với số thập phân. Để giải bài này, học sinh cần nắm vững quy tắc thực hiện các phép tính với số thập phân, đặc biệt là việc đặt dấu phẩy và cộng, trừ các hàng tương ứng.
Bài 2 đưa ra các bài toán liên quan đến việc tính thời gian, ví dụ như tính thời gian đi hết một quãng đường, tính thời gian làm việc, hoặc tính thời gian nghỉ ngơi. Để giải bài này, học sinh cần nắm vững các đơn vị đo thời gian (giây, phút, giờ, ngày, tuần, tháng, năm) và biết cách chuyển đổi giữa các đơn vị này.
Bài 3 là một bài toán tổng hợp, yêu cầu học sinh vận dụng kiến thức về quãng đường, vận tốc và thời gian để giải quyết. Công thức liên hệ giữa quãng đường (S), vận tốc (V) và thời gian (T) là: S = V x T.
| Đại lượng | Ký hiệu | Đơn vị |
|---|---|---|
| Quãng đường | S | km, m |
| Vận tốc | V | km/giờ, m/giây |
| Thời gian | T | giờ, giây |
| Công thức: S = V x T | ||
Ví dụ: Một ô tô đi từ A đến B với vận tốc 60km/giờ trong 2 giờ. Hỏi quãng đường AB dài bao nhiêu km? Giải: Quãng đường AB = Vận tốc x Thời gian = 60km/giờ x 2 giờ = 120km.
Hy vọng với bài giải chi tiết này, các em học sinh lớp 5 sẽ tự tin hơn khi giải các bài tập trong phần A. Tái hiện, củng cố trang 44 Bài tập phát triển năng lực Toán 5. Chúc các em học tốt!
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức. Hãy truy cập website của chúng tôi để khám phá thêm nhiều bài giải và tài liệu học tập hữu ích.