Chào mừng các em học sinh đến với bài giải chi tiết phần C. Vận dụng, phát triển trang 41 trong sách Bài tập phát triển năng lực Toán 5 tập 2. Bài viết này được thiết kế để giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải toán, đồng thời rèn luyện kỹ năng giải quyết vấn đề.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, cùng với các phương pháp giải khác nhau để các em có thể lựa chọn cách tiếp cận phù hợp nhất với bản thân.
a) Viết 5 số thập phân ở giữa 0,08 và 0,086 ; Cô Tâm có 15kg mơ để làm ô mai. Để làm ô mai mơ gừng chua ngọt ....
a) Viết 5 số thập phân ở giữa 0,08 và 0,086:
b) Tìm chữ số a trong các số thập phân biết:
(1) $\overline {5,6a2} $< 5,612
(2) $\overline {4,2a0} $ > 4,256
(3) 0,123 > $\overline {0,a18} $
(4) $\overline {a,345} $ < 2,001
c) So sánh hai chữ số a và b trong các số thập phân:
(1) $\overline {a,955} $ > $\overline {b,98} $
(2) $\overline {0,a17} $ = $\overline {0,b170} $
(3) $\overline {5,63a} $ < $\overline {5,63b} $
Phương pháp giải:
a) Viết 5 số thập phân lớn hơn 0,08 và bé hơn 0,086
b) Dựa vào cách so sánh hai số thập phân để tìm chữ số a thích hợp.
Lời giải chi tiết:
a) 5 số thập phân ở giữa 0,08 và 0,086 là 0,081; 0,082; 0,083; 0,084; 0,085
b) (1) Ta có 5,602 < 5,612
Vậy a = 0 thì $\overline {5,6a2} $< 5,612
(2) $\overline {4,2a0} $ > 4,256
Vậy a = 6, hoặc a = 7, hoặc a = 8, hoặc a = 9 thì $\overline {4,2a0} $ > 4,256
(3) Ta có 0,123 > 0,018
Vậy a = 0 thì 0,123 > $\overline {0,a18} $
(4) $\overline {a,345} $ < 2,001
Vậy a = 0 hoặc a = 1 thì $\overline {a,345} $ < 2,001
c) (1) Ta có $\overline {a,955} $ > $\overline {b,98} $ nên a > b
(2) Ta có $\overline {0,a17} $ = $\overline {0,b170} $ nên a = b
(3) Ta có $\overline {5,63a} $ < $\overline {5,63b} $ nên a < b
Một lát bánh mì nho có khoảng $\frac{1}{{20}}$khối lượng là nho khô.
a) Ổ bánh mì có khối lượng 500g thì có khoảng bao nhiêu gam nho khô?
b) Cần bao nhiêu ki-lô-gam nho khô để sản xuất được 200 ổ bánh mì như vậy?
Phương pháp giải:
a) Số gam nho khô = Khối lượng ổ bánh mì x $\frac{1}{{20}}$
b) Số gam nho khô để sản xuất 200 ổ bánh mì khối lượng nho khô để sản xuất một ổ bánh mì x 200
Đổi gam sang ki-lô-gam.
Lời giải chi tiết:
a) Số gam nho khô để làm một ổ bánh mì 500g là:
500 x $\frac{1}{{20}}$= 25 (gam)
b) Số ki-lô-gam nho khô cần sản xuất 200 ổ bánh mì là:
25 x 200 = 5000 (gam) = 5 kg
Đáp số: a) 25g
b) 5kg
Cô Tâm có 15kg mơ để làm ô mai. Để làm ô mai mơ gừng chua ngọt, cần cho thêm lượng đường trắng bằng $\frac{1}{2}$ lượng mơ, lượng gừng tươi bằng $\frac{1}{2}$ lượng mơ, lượn muối bằng $\frac{1}{{10}}$lượng mơ, lượng đường phèn bằng $\frac{1}{{10}}$lượng mơ. Tính khối lượng các nguyên liệu cô Tâm cần chuẩn bị thêm.
Phương pháp giải:
Bước 1: Khối lượng đường trắng = số kg mơ x $\frac{1}{2}$
Bước 2: Khối lượng gừng tươi = số kg mơ x $\frac{1}{2}$
Bước 3: Khối lượng muối = số kg mơ x $\frac{1}{{10}}$
Bước 4: Khối lượng đường phèn = số kg mơ x $\frac{1}{{10}}$
Lời giải chi tiết:
Khối lượng đường trắng để làm ô mai là:
15 x $\frac{1}{2}$= 7,5 (kg)
Khối lượng gừng tươi để làm ô mai là:
15 x $\frac{1}{2}$= 7,5 (kg)
Khối lượng muối để làm ô mai là:
15 x $\frac{1}{{10}}$ = 1,5 (kg)
Khối lượng đường phèn để làm ô mai là:
15 x $\frac{1}{{10}}$ = 1,5 (kg)
Đáp số: 7,5 kg đường trắng
7,5 kg gừng tươi
1,5 kg muối
1,5 kg đường phèn

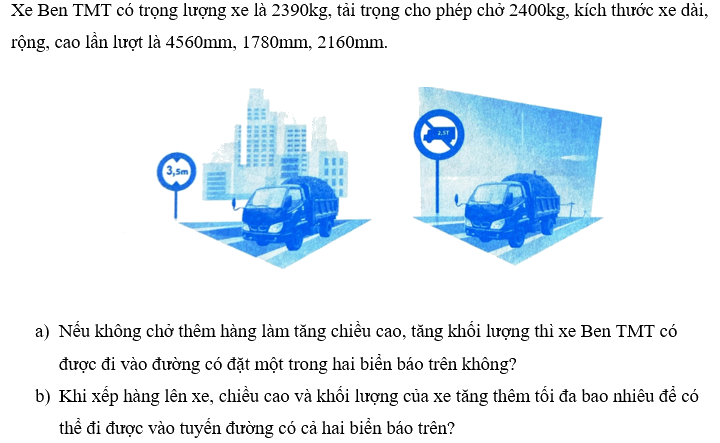
Phương pháp giải:
a) Đổi 2160 mm = ? m ; 2390kg = ? tấn
So sánh chiều cao, khối lượng của xe với thông tin trên biển báo rồi kết luận.
b) Bước 1: Chiều cao của xe tăng thêm tối đa = số chiều cao ghi trên biển – chiều cao xe ben TMT
Bước 2: Trọng lượng xe tăng thêm tối đa = số trọng lượng ghi trên biển – trọng lượng xe ben TMT
Lời giải chi tiết:
a) Đổi 2390kg = 2,39 tấn ; 2160 mm = 2,16m
Vì xe cao 2,16m < 3,5m nên xe đi được vào đường có đặt biển báo hình 1
Vì xe nặng 2,39 tấn < 2,5 tấn nên xe đi được vào đường có đặt biển báo hình 2
Vậy nếu không chở thêm hàng thì xe ben TMT được đi vào đường có đặt hai biển báo nói trên.
b) Chiều cao của xe tăng thêm tối đa là:
3,5 – 2,16 = 1,34 (m)
Trọng lượng xe tăng thêm tối đa là:
2,5 – 2,39 = 0,11 (tấn)
Đáp số: a) Xe được đi qua
b) Chiều cao tăng tối đa: 1,34m
Trọng lượng tăng tối đa: 0,11 tấn
a) Viết 5 số thập phân ở giữa 0,08 và 0,086:
b) Tìm chữ số a trong các số thập phân biết:
(1) $\overline {5,6a2} $< 5,612
(2) $\overline {4,2a0} $ > 4,256
(3) 0,123 > $\overline {0,a18} $
(4) $\overline {a,345} $ < 2,001
c) So sánh hai chữ số a và b trong các số thập phân:
(1) $\overline {a,955} $ > $\overline {b,98} $
(2) $\overline {0,a17} $ = $\overline {0,b170} $
(3) $\overline {5,63a} $ < $\overline {5,63b} $
Phương pháp giải:
a) Viết 5 số thập phân lớn hơn 0,08 và bé hơn 0,086
b) Dựa vào cách so sánh hai số thập phân để tìm chữ số a thích hợp.
Lời giải chi tiết:
a) 5 số thập phân ở giữa 0,08 và 0,086 là 0,081; 0,082; 0,083; 0,084; 0,085
b) (1) Ta có 5,602 < 5,612
Vậy a = 0 thì $\overline {5,6a2} $< 5,612
(2) $\overline {4,2a0} $ > 4,256
Vậy a = 6, hoặc a = 7, hoặc a = 8, hoặc a = 9 thì $\overline {4,2a0} $ > 4,256
(3) Ta có 0,123 > 0,018
Vậy a = 0 thì 0,123 > $\overline {0,a18} $
(4) $\overline {a,345} $ < 2,001
Vậy a = 0 hoặc a = 1 thì $\overline {a,345} $ < 2,001
c) (1) Ta có $\overline {a,955} $ > $\overline {b,98} $ nên a > b
(2) Ta có $\overline {0,a17} $ = $\overline {0,b170} $ nên a = b
(3) Ta có $\overline {5,63a} $ < $\overline {5,63b} $ nên a < b
Cô Tâm có 15kg mơ để làm ô mai. Để làm ô mai mơ gừng chua ngọt, cần cho thêm lượng đường trắng bằng $\frac{1}{2}$ lượng mơ, lượng gừng tươi bằng $\frac{1}{2}$ lượng mơ, lượn muối bằng $\frac{1}{{10}}$lượng mơ, lượng đường phèn bằng $\frac{1}{{10}}$lượng mơ. Tính khối lượng các nguyên liệu cô Tâm cần chuẩn bị thêm.
Phương pháp giải:
Bước 1: Khối lượng đường trắng = số kg mơ x $\frac{1}{2}$
Bước 2: Khối lượng gừng tươi = số kg mơ x $\frac{1}{2}$
Bước 3: Khối lượng muối = số kg mơ x $\frac{1}{{10}}$
Bước 4: Khối lượng đường phèn = số kg mơ x $\frac{1}{{10}}$
Lời giải chi tiết:
Khối lượng đường trắng để làm ô mai là:
15 x $\frac{1}{2}$= 7,5 (kg)
Khối lượng gừng tươi để làm ô mai là:
15 x $\frac{1}{2}$= 7,5 (kg)
Khối lượng muối để làm ô mai là:
15 x $\frac{1}{{10}}$ = 1,5 (kg)
Khối lượng đường phèn để làm ô mai là:
15 x $\frac{1}{{10}}$ = 1,5 (kg)
Đáp số: 7,5 kg đường trắng
7,5 kg gừng tươi
1,5 kg muối
1,5 kg đường phèn
Một lát bánh mì nho có khoảng $\frac{1}{{20}}$khối lượng là nho khô.
a) Ổ bánh mì có khối lượng 500g thì có khoảng bao nhiêu gam nho khô?
b) Cần bao nhiêu ki-lô-gam nho khô để sản xuất được 200 ổ bánh mì như vậy?
Phương pháp giải:
a) Số gam nho khô = Khối lượng ổ bánh mì x $\frac{1}{{20}}$
b) Số gam nho khô để sản xuất 200 ổ bánh mì khối lượng nho khô để sản xuất một ổ bánh mì x 200
Đổi gam sang ki-lô-gam.
Lời giải chi tiết:
a) Số gam nho khô để làm một ổ bánh mì 500g là:
500 x $\frac{1}{{20}}$= 25 (gam)
b) Số ki-lô-gam nho khô cần sản xuất 200 ổ bánh mì là:
25 x 200 = 5000 (gam) = 5 kg
Đáp số: a) 25g
b) 5kg

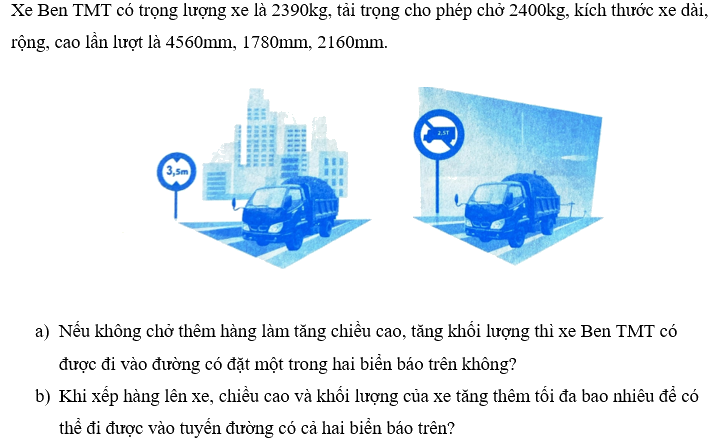
Phương pháp giải:
a) Đổi 2160 mm = ? m ; 2390kg = ? tấn
So sánh chiều cao, khối lượng của xe với thông tin trên biển báo rồi kết luận.
b) Bước 1: Chiều cao của xe tăng thêm tối đa = số chiều cao ghi trên biển – chiều cao xe ben TMT
Bước 2: Trọng lượng xe tăng thêm tối đa = số trọng lượng ghi trên biển – trọng lượng xe ben TMT
Lời giải chi tiết:
a) Đổi 2390kg = 2,39 tấn ; 2160 mm = 2,16m
Vì xe cao 2,16m < 3,5m nên xe đi được vào đường có đặt biển báo hình 1
Vì xe nặng 2,39 tấn < 2,5 tấn nên xe đi được vào đường có đặt biển báo hình 2
Vậy nếu không chở thêm hàng thì xe ben TMT được đi vào đường có đặt hai biển báo nói trên.
b) Chiều cao của xe tăng thêm tối đa là:
3,5 – 2,16 = 1,34 (m)
Trọng lượng xe tăng thêm tối đa là:
2,5 – 2,39 = 0,11 (tấn)
Đáp số: a) Xe được đi qua
b) Chiều cao tăng tối đa: 1,34m
Trọng lượng tăng tối đa: 0,11 tấn
Phần C. Vận dụng, phát triển trang 41 trong sách Bài tập phát triển năng lực Toán 5 tập 2 thường chứa các bài toán đòi hỏi học sinh phải vận dụng kiến thức đã học vào giải quyết các tình huống thực tế, hoặc mở rộng kiến thức để giải quyết các bài toán phức tạp hơn. Các bài toán này không chỉ giúp học sinh củng cố kiến thức mà còn phát triển tư duy logic, khả năng phân tích và giải quyết vấn đề.
Để giúp các em hiểu rõ hơn về nội dung và phương pháp giải các bài toán trong phần C, chúng ta sẽ đi vào phân tích chi tiết từng bài toán:
Đề bài: (Nêu rõ đề bài của bài toán)
Phân tích: Bài toán này yêu cầu chúng ta (Phân tích yêu cầu của bài toán, xác định kiến thức cần sử dụng).
Lời giải: (Trình bày lời giải chi tiết, rõ ràng, dễ hiểu. Có thể sử dụng sơ đồ, hình vẽ minh họa nếu cần thiết).
Kết luận: (Nêu kết quả cuối cùng của bài toán).
Đề bài: (Nêu rõ đề bài của bài toán)
Phân tích: Bài toán này yêu cầu chúng ta (Phân tích yêu cầu của bài toán, xác định kiến thức cần sử dụng).
Lời giải: (Trình bày lời giải chi tiết, rõ ràng, dễ hiểu. Có thể sử dụng sơ đồ, hình vẽ minh họa nếu cần thiết).
Kết luận: (Nêu kết quả cuối cùng của bài toán).
Trong quá trình giải các bài toán phần C, các em có thể gặp một số phương pháp giải toán thường gặp sau:
Ngoài việc giải các bài toán trong sách bài tập, các em cũng nên dành thời gian để mở rộng kiến thức bằng cách:
Để nắm vững kiến thức và kỹ năng giải toán, các em cần luyện tập thường xuyên. Hãy giải các bài toán trong sách bài tập, các đề thi thử, và các bài toán tự luyện. Đồng thời, hãy tự kiểm tra và đánh giá kết quả của mình để tìm ra những điểm cần cải thiện.
Khi gặp khó khăn trong quá trình giải toán, đừng nản lòng. Hãy kiên trì, tìm tòi, và học hỏi từ những người khác. Hãy nhớ rằng, việc giải toán không chỉ là để đạt điểm cao mà còn là để rèn luyện tư duy và phát triển bản thân.
| Kiến thức | Mô tả |
|---|---|
| Phép cộng, trừ, nhân, chia | Các phép toán cơ bản cần nắm vững. |
| Phân số | Khái niệm, tính chất, các phép toán với phân số. |
| Số thập phân | Khái niệm, tính chất, các phép toán với số thập phân. |
| Hình học | Các hình cơ bản, tính diện tích, chu vi. |
Hy vọng rằng bài viết này sẽ giúp các em giải quyết thành công phần C. Vận dụng, phát triển trang 41 Bài tập phát triển năng lực Toán 5 tập 2. Chúc các em học tập tốt!