Chào mừng các em học sinh đến với bài giải chi tiết Giải phần B. Kết nối trang 37 Bài tập phát triển năng lực Toán 5 tập 2. Bài viết này sẽ cung cấp cho các em lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giaitoan.edu.vn là website học toán online uy tín, cung cấp đầy đủ các bài giải Toán 5 tập 1, tập 2 và các lớp học khác. Chúng tôi luôn cập nhật nội dung mới nhất và đảm bảo tính chính xác cao.
Một ô tô đi từ A đến B với vận tốc 65km/giờ. Cùng lúc đó, một xe máy đi từ B đến A với vận tốc 40km/giờ. Quãng đường Hà Nội – Lạng Sơn dài 158,4km ...
Một ô tô đi từ A đến B với vận tốc 65km/giờ. Cùng lúc đó, một xe máy đi từ B đến A với vận tốc 40km/giờ. Ô tô và xe máy gặp nhau tại một địa điểm cách A là 162,5km. Tính quãng đường AB.
Phương pháp giải:
Bước 1: Thời gian hai xe gặp nhau = quãng đường từ điểm gặp nhau đến A : vận tốc ô tô đi từ A
Bước 2: Tổng vận tốc của hai xe = vận tốc của ô tô + vận tốc của xe máy
Bước 3: Quãng đường AB = tổng vận tốc của hai xe x thời gian hai xe gặp nhau
Lời giải chi tiết:
Thời gian để hai xe đi đến chỗ gặp nhau là:
162,5 : 65 = 2,5 (giờ)
Tổng vận tốc của hai xe là:
65 + 40 = 105 (km/giờ)
Quãng đường AB dài là:
105 x 2,5 = 262,5 (km)
Đáp số: 262,5 km
Quãng đường Hà Nội – Lạng Sơn dài 158,4km. Một ô tô đi từ Hà Nội đến Lạng Sơn với vận tốc 48km/giờ, cùng lúc đó một người đi xe máy đi từ Lạng Sơn đến Hà Nội với vận tốc 40km/giờ. Hỏi kể từ lúc bắt đầu đi, sau bao lâu ô tô gặp xe máy?
Phương pháp giải:
Bước 1: Tổng vận tốc của hai xe = vận tốc của ô tô + vận tốc của xe máy
Bước 2: Thời gian để hai xe gặp nhau = Quãng đường Hà Nội – Lạng Sơn : tổng vận tốc của hai xe
Lời giải chi tiết:
Tổng vận tốc của hai xe là:
48 + 40 = 88 (km/giờ)
Thời gian để hai xe gặp nhau là:
158,4 : 88 = 1,8 giờ)
Đáp số: 1,8 giờ
Viết các phân số sau thành phân số thập phân:
Viết các phân số sau thành phân số thập phân:
$\frac{1}{2}$= ..............................
$\frac{{27}}{{150}}$= ...............
$\frac{{1377}}{{2025}}$= .........
$\frac{{5184}}{{20736}}$= .......
Phương pháp giải:
Nhân hoặc chia cả tử số và mẫu số của các phân số đã cho với một số thích hợp để được phân số thập phân có mẫu là 10; 100; 1000; …
Lời giải chi tiết:
$\frac{1}{2}$=$\frac{{1 \times 5}}{{2 \times 5}} = \frac{5}{{10}}$;
$\frac{{27}}{{150}}$= $\frac{{27:3}}{{150:3}} = \frac{9}{{50}} = \frac{{9 \times 2}}{{50 \times 2}} = \frac{{18}}{{100}}$;
$\frac{{1377}}{{2025}}$=$\frac{{1377:81}}{{2025:81}} = \frac{{17}}{{25}} = \frac{{17 \times 4}}{{25 \times 4}} = \frac{{68}}{{100}}$;
$\frac{{5184}}{{20736}}$= $\frac{{5184:5184}}{{20736:5184}} = \frac{1}{4} = \frac{{1 \times 25}}{{4 \times 25}} = \frac{{25}}{{100}}$
Điền chữ số thích hợp vào ô trống để:
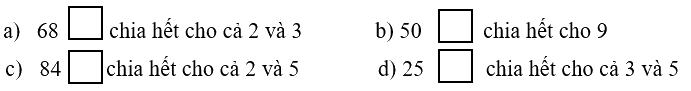
Phương pháp giải:
- Các số có chữ số tận cùng là 0, 2, 4, 6, 8 thì chia hết cho 2.- Các số có chữ số tận cùng là 0, 5 thì chia hết cho 5.- Các số có tổng các chữ số chia hết chia hết cho 3 thì chia hết cho 3.- Các số có tổng các chữ số chia hết chia hết cho 9 thì chia hết cho 9.
Lời giải chi tiết:
a) Để số 68… chia hết cho cả 2 và 3 thì 6 + 8 +… = 14 + …. Chia hết cho cả 2 và 3
Vậy ta có thể viết số 4 vào chỗ chấm
Vậy 684 chia hết cho cả 2 và 3
b) Để số 50… chia hết cho 9 thì 5 + 0 + …. chia hết cho 9
Vậy ta có thể viết số 4 vào chỗ chấm
Vậy 504 chia hết cho 9
c) 84….chia hết cho cả 2 và 5 thì chữ số tạn cùng bằng 0.
Vậy ta viết số 0 vào chỗ chấm
Vậy 840 chia hết cho cả 2 và 5
d) 25….chia hết cho cả 3 và 5 thì 2 + 5 + ….chia hết cho cả 3 và 5
Vậy ta có thể viết số 5 vào chỗ chấm
Vậy 255 chia hết cho cả 3 và 5
Viết vào ô trống (theo mẫu):

Phương pháp giải:
- Muốn tính vận tốc ta lấy quãng đường chia cho thời gian
- Muốn tính quãng đường ta lấy vận tốc nhân với thời gian
- Muốn tính thời gian ta lấy quãng đường chia cho vận tốc
Lời giải chi tiết:
Cột 3: v = 440 : 4 = 110 km/giờ
Cột 4: s = 100 x 30 = 3000 m
Cột 5: t = 90 000 : 12,5 = 7200 giây
Cột 6: Đổi 2 giờ 30 phút = 150 phút
v = 150 : 150 = 1 km/phút

Vậy ta có kết quả sau:
Viết vào ô trống (theo mẫu):

Phương pháp giải:
- Muốn tính vận tốc ta lấy quãng đường chia cho thời gian
- Muốn tính quãng đường ta lấy vận tốc nhân với thời gian
- Muốn tính thời gian ta lấy quãng đường chia cho vận tốc
Lời giải chi tiết:
Cột 3: v = 440 : 4 = 110 km/giờ
Cột 4: s = 100 x 30 = 3000 m
Cột 5: t = 90 000 : 12,5 = 7200 giây
Cột 6: Đổi 2 giờ 30 phút = 150 phút
v = 150 : 150 = 1 km/phút

Vậy ta có kết quả sau:
Một ô tô đi từ A đến B với vận tốc 65km/giờ. Cùng lúc đó, một xe máy đi từ B đến A với vận tốc 40km/giờ. Ô tô và xe máy gặp nhau tại một địa điểm cách A là 162,5km. Tính quãng đường AB.
Phương pháp giải:
Bước 1: Thời gian hai xe gặp nhau = quãng đường từ điểm gặp nhau đến A : vận tốc ô tô đi từ A
Bước 2: Tổng vận tốc của hai xe = vận tốc của ô tô + vận tốc của xe máy
Bước 3: Quãng đường AB = tổng vận tốc của hai xe x thời gian hai xe gặp nhau
Lời giải chi tiết:
Thời gian để hai xe đi đến chỗ gặp nhau là:
162,5 : 65 = 2,5 (giờ)
Tổng vận tốc của hai xe là:
65 + 40 = 105 (km/giờ)
Quãng đường AB dài là:
105 x 2,5 = 262,5 (km)
Đáp số: 262,5 km
Quãng đường Hà Nội – Lạng Sơn dài 158,4km. Một ô tô đi từ Hà Nội đến Lạng Sơn với vận tốc 48km/giờ, cùng lúc đó một người đi xe máy đi từ Lạng Sơn đến Hà Nội với vận tốc 40km/giờ. Hỏi kể từ lúc bắt đầu đi, sau bao lâu ô tô gặp xe máy?
Phương pháp giải:
Bước 1: Tổng vận tốc của hai xe = vận tốc của ô tô + vận tốc của xe máy
Bước 2: Thời gian để hai xe gặp nhau = Quãng đường Hà Nội – Lạng Sơn : tổng vận tốc của hai xe
Lời giải chi tiết:
Tổng vận tốc của hai xe là:
48 + 40 = 88 (km/giờ)
Thời gian để hai xe gặp nhau là:
158,4 : 88 = 1,8 giờ)
Đáp số: 1,8 giờ
Điền chữ số thích hợp vào ô trống để:
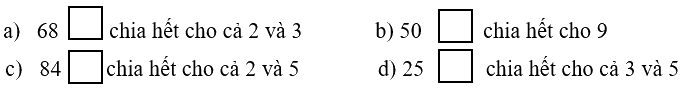
Phương pháp giải:
- Các số có chữ số tận cùng là 0, 2, 4, 6, 8 thì chia hết cho 2.- Các số có chữ số tận cùng là 0, 5 thì chia hết cho 5.- Các số có tổng các chữ số chia hết chia hết cho 3 thì chia hết cho 3.- Các số có tổng các chữ số chia hết chia hết cho 9 thì chia hết cho 9.
Lời giải chi tiết:
a) Để số 68… chia hết cho cả 2 và 3 thì 6 + 8 +… = 14 + …. Chia hết cho cả 2 và 3
Vậy ta có thể viết số 4 vào chỗ chấm
Vậy 684 chia hết cho cả 2 và 3
b) Để số 50… chia hết cho 9 thì 5 + 0 + …. chia hết cho 9
Vậy ta có thể viết số 4 vào chỗ chấm
Vậy 504 chia hết cho 9
c) 84….chia hết cho cả 2 và 5 thì chữ số tạn cùng bằng 0.
Vậy ta viết số 0 vào chỗ chấm
Vậy 840 chia hết cho cả 2 và 5
d) 25….chia hết cho cả 3 và 5 thì 2 + 5 + ….chia hết cho cả 3 và 5
Vậy ta có thể viết số 5 vào chỗ chấm
Vậy 255 chia hết cho cả 3 và 5
Viết các phân số sau thành phân số thập phân:
Viết các phân số sau thành phân số thập phân:
$\frac{1}{2}$= ..............................
$\frac{{27}}{{150}}$= ...............
$\frac{{1377}}{{2025}}$= .........
$\frac{{5184}}{{20736}}$= .......
Phương pháp giải:
Nhân hoặc chia cả tử số và mẫu số của các phân số đã cho với một số thích hợp để được phân số thập phân có mẫu là 10; 100; 1000; …
Lời giải chi tiết:
$\frac{1}{2}$=$\frac{{1 \times 5}}{{2 \times 5}} = \frac{5}{{10}}$;
$\frac{{27}}{{150}}$= $\frac{{27:3}}{{150:3}} = \frac{9}{{50}} = \frac{{9 \times 2}}{{50 \times 2}} = \frac{{18}}{{100}}$;
$\frac{{1377}}{{2025}}$=$\frac{{1377:81}}{{2025:81}} = \frac{{17}}{{25}} = \frac{{17 \times 4}}{{25 \times 4}} = \frac{{68}}{{100}}$;
$\frac{{5184}}{{20736}}$= $\frac{{5184:5184}}{{20736:5184}} = \frac{1}{4} = \frac{{1 \times 25}}{{4 \times 25}} = \frac{{25}}{{100}}$
Bài tập phần B trong sách Toán 5 tập 2, Kết nối tri thức trang 37 tập trung vào việc ôn luyện và củng cố các kiến thức đã học về các phép tính với số thập phân, đặc biệt là các bài toán liên quan đến ứng dụng thực tế. Mục tiêu chính là giúp học sinh rèn luyện kỹ năng giải toán, tư duy logic và khả năng vận dụng kiến thức vào giải quyết các vấn đề trong cuộc sống.
Bài tập phần B bao gồm các dạng toán khác nhau, đòi hỏi học sinh phải nắm vững các kiến thức cơ bản và kỹ năng giải toán. Dưới đây là phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh tính nhẩm nhanh các phép tính với số thập phân. Để làm tốt bài tập này, học sinh cần nắm vững bảng cửu chương, các quy tắc cộng, trừ, nhân, chia số thập phân và luyện tập thường xuyên.
Bài tập này yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia số thập phân. Học sinh cần chú ý đến vị trí của dấu phẩy và thực hiện các phép tính một cách cẩn thận.
Đây là dạng toán phổ biến trong chương trình Toán 5. Để giải bài toán có lời văn, học sinh cần đọc kỹ đề bài, xác định được các dữ kiện và yêu cầu của bài toán, sau đó lập kế hoạch giải và thực hiện các phép tính cần thiết.
Bài toán: Một cửa hàng có 35,5 kg gạo tẻ và 28,7 kg gạo nếp. Hỏi cửa hàng có tất cả bao nhiêu ki-lô-gam gạo?
Giải:
Số ki-lô-gam gạo cửa hàng có tất cả là:
35,5 + 28,7 = 64,2 (kg)
Đáp số: 64,2 kg
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 5:
Giải phần B. Kết nối trang 37 Toán 5 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết và các phương pháp giải hiệu quả trên đây, các em sẽ tự tin giải tốt bài tập này và đạt kết quả cao trong môn Toán.