Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong phần B, trang 20 sách Toán 5 Kết nối tri thức với thực tiễn. Chúng tôi giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán một cách hiệu quả.
Giaitoan.edu.vn là nền tảng học toán online uy tín, cung cấp đầy đủ các bài giải Toán 5 Kết nối, đáp ứng nhu cầu học tập của học sinh.
Viết số thích hợp vào chỗ chấm: 415m = …………hm………...m Trên tuyến đường sắt Thống Nhất, quãng đường Hà Nội – Vinh dài 319km...
Trên tuyến đường sắt Thống Nhất, quãng đường Hà Nội – Vinh dài 319km, Vinh – Nha Trang dài 996km, Nha Trang – Thành phố Hồ Chí Minh dài 411km.
a) Quãng đường sắt Hà Nội – Nha Trang dài bao nhiêu ki-lô-mét?
b) Quãng đường sắt Vinh – Thành Phố Hồ Chí Minh dài bao nhiêu ki-lô-mét?
Phương pháp giải:
a) Quãng đường sắt Hà Nội – Nha Trang = quãng đường Hà Nội – Vinh + quãng đường Vinh – Nha Trang
b) Quãng đường sắt Vinh – Thành Phố Hồ Chí Minh = quãng đường Vinh – Nha Trang + quãng đường Nha Trang – Thành Phố Hồ Chí Minh
Lời giải chi tiết:
Tóm tắt:
Hà Nội – Vinh : 319km
Vinh – Nha Trang : 996km
Nha Trang – Tp Hồ Chí Minh : 411km
a) Hà Nội – Nha Trang : ……km?
b) Vinh – Tp Hồ Chí Minh :…….km?
Bài giải
a) Quãng đường sắt từ Hà Nội – Nha Trang dài:
319 + 996 = 1315 (km)
b) Quãng đường sắt từ Vinh – Thành Phố Hồ Chí Minh dài:
996 + 411 = 1407 (km)
Đáp số: a) Hà Nội – Nha Trang: 1315km
b) Vinh – Tp Hồ Chí Minh: 1407km
Một kho vật liệu xây dựng nhận hàng để giao cho các địa lí. Lần thứ nhất nhận về 35 tấn 28 yến hàng, lần thứ hai nhận về 32 tấn 220kg hàng. Sau đó người ta dùng xe ô tô tải để chuyển hết số hàng đó, biết rằng cứ 4 xe thì chở được 100 tạ. Hỏi cần phải dùng bao nhiêu xe? (Biết các xe chở được số hàng như nhau)
Phương pháp giải:
- Đổi đơn vị sang kg
- Tìm tổng hàng mà đại lí nhận về sau 2 lần
- Tìm 1 xe chở được số tạ hàng = Số tạ 4 xe chở được : 4
- Số xe cần dùng = Tổng số tấn hàng mà đại lí nhận về : số kg hàng 1 xe chở
Lời giải chi tiết:
35 tấn 28 yến = 35 280 kg
32 tấn 220 kg = 32 220 kg
Tổng số tấn hàng mà đại lí nhận về sau 2 lần là:
35 280 + 32 220 = 67500 (kg)
1 xe chở được số ki-lô-gam là
100 : 4 = 25 (tạ) = 2500 kg
Số chiếc xe cần dùng là:
67500 : 2500 = 27 (xe)
Đáp số: 27 xe
Một cửa hàng ngày thứ nhất bán được 120kg gạo, ngày thứ bán được số ki-lô-gam gạo gấp đôi ngày thứ nhất ngày thứ ba bán được số ki-lô-gam gạo bằng trung bình cộng của ngày thứ nhất và ngày thứ hai. Hỏi cửa hàng đó đã bán được tất cả bao nhiêu yến gạo?
Phương pháp giải:
Bước 1: Số gạo bán ngày thứ hai = Số gạo bán ngày thứ nhất x 2
Bước 2: Số gạo ngày thứ ba = (Số gạo bán ngày thứ nhất + số gạo bán ngày thứ hai) : 2
Bước 3: Tìm số kg gạo cửa hàng đó bán được trong 3 ngày
Bước 4: Đổi kg sang yến
Lời giải chi tiết:
Ngày thứ hai bán được số kg gạo là:
120 x 2 = 240 (kg)
Ngày thứ ba bán được số kg là:
(120 + 240) : 2 = 180 (kg)
Của hàng đó bán được tất cả số yến gạo là:
120 + 240 +180 = 540 (kg)
Đổi 540kg = 54 yến
Đáp số: 54 yến gạo
Mảnh vườn nhà bác Nam có diện tích là 2hm2 85m2. Mảnh vườn nhà bác Cường lớn hơn mảnh vườn nhà bác Nam 115m2. Tính diện tích mảnh vườn nhà bác Cường theo đơn vị đo đề-ca-mét-vuông.
Phương pháp giải:
Đổi 2hm2 85m2 = …...m2
Diện tích mảnh vườn nhà bác Cường = Diện tích vườn nhà bác Nam + 115
Đổi sang đơn vị đề-ca-mét vuông
Lời giải chi tiết:
Đổi 2hm2 85m2 = 20 085 m2
Diện tích mảnh vườn nhà bác Cường là:
20085 + 115 = 20200 (m2)
Đổi 20200m2 = 202dam2
Đáp số: 202dam2
Viết số thích hợp vào chỗ chấm:

Phương pháp giải:
Áp dụng các cách đổi:
1kg = 1000g 1kg = 10hg
1kg =100dag 1 tấn = 1000kg
Lời giải chi tiết:
6005g = 6kg 5g 142hg = 14kg 2hg
215dag = 2kg 15dag 3013kg = 3tấn 13kg
Viết số thích hợp vào chỗ chấm:
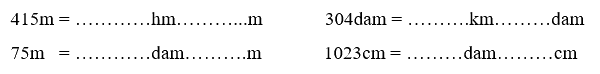
Phương pháp giải:
Áp dụng các cách đổi:
1hm = 100m 1km = 100dam
1dam = 10m 1dam = 1000cm
Lời giải chi tiết:
415m = 4hm 15m 304dam = 3km 4dam
75m = 7dam 5m 1023cm = 1dam 23cm
Viết số thích hợp vào chỗ chấm:
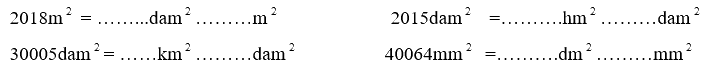
Phương pháp giải:
Áp dụng các cách đổi:
1dam2 = 100m2 1hm2 = 100dam2
1 km2 = 10000dam2 1dm2 = 10000mm2
Lời giải chi tiết:

Viết số thích hợp vào chỗ chấm:
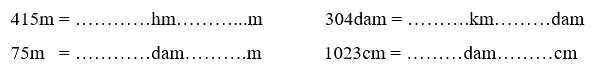
Phương pháp giải:
Áp dụng các cách đổi:
1hm = 100m 1km = 100dam
1dam = 10m 1dam = 1000cm
Lời giải chi tiết:
415m = 4hm 15m 304dam = 3km 4dam
75m = 7dam 5m 1023cm = 1dam 23cm
Trên tuyến đường sắt Thống Nhất, quãng đường Hà Nội – Vinh dài 319km, Vinh – Nha Trang dài 996km, Nha Trang – Thành phố Hồ Chí Minh dài 411km.
a) Quãng đường sắt Hà Nội – Nha Trang dài bao nhiêu ki-lô-mét?
b) Quãng đường sắt Vinh – Thành Phố Hồ Chí Minh dài bao nhiêu ki-lô-mét?
Phương pháp giải:
a) Quãng đường sắt Hà Nội – Nha Trang = quãng đường Hà Nội – Vinh + quãng đường Vinh – Nha Trang
b) Quãng đường sắt Vinh – Thành Phố Hồ Chí Minh = quãng đường Vinh – Nha Trang + quãng đường Nha Trang – Thành Phố Hồ Chí Minh
Lời giải chi tiết:
Tóm tắt:
Hà Nội – Vinh : 319km
Vinh – Nha Trang : 996km
Nha Trang – Tp Hồ Chí Minh : 411km
a) Hà Nội – Nha Trang : ……km?
b) Vinh – Tp Hồ Chí Minh :…….km?
Bài giải
a) Quãng đường sắt từ Hà Nội – Nha Trang dài:
319 + 996 = 1315 (km)
b) Quãng đường sắt từ Vinh – Thành Phố Hồ Chí Minh dài:
996 + 411 = 1407 (km)
Đáp số: a) Hà Nội – Nha Trang: 1315km
b) Vinh – Tp Hồ Chí Minh: 1407km
Viết số thích hợp vào chỗ chấm:

Phương pháp giải:
Áp dụng các cách đổi:
1kg = 1000g 1kg = 10hg
1kg =100dag 1 tấn = 1000kg
Lời giải chi tiết:
6005g = 6kg 5g 142hg = 14kg 2hg
215dag = 2kg 15dag 3013kg = 3tấn 13kg
Một kho vật liệu xây dựng nhận hàng để giao cho các địa lí. Lần thứ nhất nhận về 35 tấn 28 yến hàng, lần thứ hai nhận về 32 tấn 220kg hàng. Sau đó người ta dùng xe ô tô tải để chuyển hết số hàng đó, biết rằng cứ 4 xe thì chở được 100 tạ. Hỏi cần phải dùng bao nhiêu xe? (Biết các xe chở được số hàng như nhau)
Phương pháp giải:
- Đổi đơn vị sang kg
- Tìm tổng hàng mà đại lí nhận về sau 2 lần
- Tìm 1 xe chở được số tạ hàng = Số tạ 4 xe chở được : 4
- Số xe cần dùng = Tổng số tấn hàng mà đại lí nhận về : số kg hàng 1 xe chở
Lời giải chi tiết:
35 tấn 28 yến = 35 280 kg
32 tấn 220 kg = 32 220 kg
Tổng số tấn hàng mà đại lí nhận về sau 2 lần là:
35 280 + 32 220 = 67500 (kg)
1 xe chở được số ki-lô-gam là
100 : 4 = 25 (tạ) = 2500 kg
Số chiếc xe cần dùng là:
67500 : 2500 = 27 (xe)
Đáp số: 27 xe
Một cửa hàng ngày thứ nhất bán được 120kg gạo, ngày thứ bán được số ki-lô-gam gạo gấp đôi ngày thứ nhất ngày thứ ba bán được số ki-lô-gam gạo bằng trung bình cộng của ngày thứ nhất và ngày thứ hai. Hỏi cửa hàng đó đã bán được tất cả bao nhiêu yến gạo?
Phương pháp giải:
Bước 1: Số gạo bán ngày thứ hai = Số gạo bán ngày thứ nhất x 2
Bước 2: Số gạo ngày thứ ba = (Số gạo bán ngày thứ nhất + số gạo bán ngày thứ hai) : 2
Bước 3: Tìm số kg gạo cửa hàng đó bán được trong 3 ngày
Bước 4: Đổi kg sang yến
Lời giải chi tiết:
Ngày thứ hai bán được số kg gạo là:
120 x 2 = 240 (kg)
Ngày thứ ba bán được số kg là:
(120 + 240) : 2 = 180 (kg)
Của hàng đó bán được tất cả số yến gạo là:
120 + 240 +180 = 540 (kg)
Đổi 540kg = 54 yến
Đáp số: 54 yến gạo
Viết số thích hợp vào chỗ chấm:
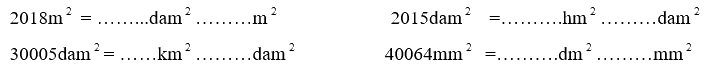
Phương pháp giải:
Áp dụng các cách đổi:
1dam2 = 100m2 1hm2 = 100dam2
1 km2 = 10000dam2 1dm2 = 10000mm2
Lời giải chi tiết:

Mảnh vườn nhà bác Nam có diện tích là 2hm2 85m2. Mảnh vườn nhà bác Cường lớn hơn mảnh vườn nhà bác Nam 115m2. Tính diện tích mảnh vườn nhà bác Cường theo đơn vị đo đề-ca-mét-vuông.
Phương pháp giải:
Đổi 2hm2 85m2 = …...m2
Diện tích mảnh vườn nhà bác Cường = Diện tích vườn nhà bác Nam + 115
Đổi sang đơn vị đề-ca-mét vuông
Lời giải chi tiết:
Đổi 2hm2 85m2 = 20 085 m2
Diện tích mảnh vườn nhà bác Cường là:
20085 + 115 = 20200 (m2)
Đổi 20200m2 = 202dam2
Đáp số: 202dam2
Phần B của bài học trang 20 trong sách Toán 5 Kết nối tri thức tập trung vào việc củng cố kiến thức về các phép tính với phân số, đặc biệt là các bài toán liên quan đến so sánh phân số, rút gọn phân số và thực hiện các phép cộng, trừ phân số với các mẫu số khác nhau. Việc nắm vững kiến thức này là nền tảng quan trọng để học sinh tiếp cận các bài toán phức tạp hơn trong chương trình Toán 5.
Bài 1 yêu cầu học sinh so sánh các phân số khác nhau. Để so sánh phân số, học sinh có thể thực hiện một trong các cách sau:
Ví dụ: So sánh 2/3 và 3/4. Quy đồng mẫu số: 2/3 = 8/12 và 3/4 = 9/12. Vì 8/12 < 9/12 nên 2/3 < 3/4.
Rút gọn phân số là việc chia cả tử số và mẫu số của phân số cho ước chung lớn nhất của chúng. Việc rút gọn phân số giúp phân số trở nên đơn giản hơn, dễ hiểu hơn và dễ dàng thực hiện các phép tính sau này.
Ví dụ: Rút gọn phân số 12/18. Ước chung lớn nhất của 12 và 18 là 6. Chia cả tử số và mẫu số cho 6: 12/6 = 2 và 18/6 = 3. Vậy 12/18 = 2/3.
Để cộng hoặc trừ hai phân số, chúng ta cần quy đồng mẫu số của hai phân số đó. Sau khi quy đồng, ta cộng hoặc trừ các tử số và giữ nguyên mẫu số.
Ví dụ: Tính 1/2 + 1/3. Quy đồng mẫu số: 1/2 = 3/6 và 1/3 = 2/6. Cộng hai phân số: 3/6 + 2/6 = 5/6.
Kiến thức về phân số được ứng dụng rộng rãi trong cuộc sống hàng ngày, ví dụ như khi chia sẻ đồ ăn, đo lường, tính toán tỷ lệ, và nhiều tình huống khác. Việc nắm vững kiến thức này giúp học sinh giải quyết các vấn đề thực tế một cách hiệu quả.
Giaitoan.edu.vn cam kết cung cấp các bài giải Toán 5 Kết nối chính xác, dễ hiểu và phù hợp với trình độ của học sinh. Chúng tôi luôn cập nhật các bài giải mới nhất và cung cấp các công cụ hỗ trợ học tập hữu ích. Hãy truy cập giaitoan.edu.vn để học toán online hiệu quả và đạt kết quả tốt nhất!
| Bước | Nội dung |
|---|---|
| 1 | Đọc kỹ đề bài và xác định yêu cầu. |
| 2 | Quy đồng mẫu số (nếu cần). |
| 3 | Thực hiện phép tính (cộng, trừ, so sánh, rút gọn). |
| 4 | Kiểm tra lại kết quả. |