Chào mừng các em học sinh đến với bài giải chi tiết phần C. Vận dụng, phát triển trang 34 trong sách Bài tập phát triển năng lực Toán 5 tập 2. Bài viết này được thiết kế để giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải toán, đồng thời rèn luyện kỹ năng giải quyết vấn đề.
Giaitoan.edu.vn cung cấp lời giải chính xác, dễ hiểu, cùng với các giải thích chi tiết để các em có thể tự học và nắm vững kiến thức.
Có một loài ve dài chỉ khoảng 0,7mm (bằng 1 hạt vừng) nhưng mỗi giây .... Chúng ta thường được nghe câu thành ngữ "Nhanh như cắt". Vậy chim cắt nhanh đến mức nào?
Chúng ta thường được nghe câu thành ngữ "Nhanh như cắt". Vậy chim cắt nhanh đến mức nào?
Một con chim cắt Bắc Cực – loài chim săn mồi – có thể đạt đến vận tốc 58m/giây. Khi săn mồi, chim cắt có thể tìm đến vị trí rất cao sau đó lợi dụng trọng lực để lao xuống con mồi bên dưới.
a) Nếu lao từ độ cao 522m xuống mặt đất thì con chim này mất bao nhiêu thời gian?
b) Một thử nghiệm khác cho thấy chim cắt còn có thể đạt được tốc độ 82m/giây khi được thả từ độ cao 4182m. Tính thời gian con chim này chạm đến mặt đất khi được thả từ độ cao đó.
Phương pháp giải:
a) Tính thời gian để con chim lao xuống mặt đất = độ cao lao xuống : vận tốc
b) Tính thời gian để con chim chạm mặt đất = độ cao: tốc độ chim cắt đạt được
Lời giải chi tiết:
a) Thời gian để con chim lao xuống mặt đất là:
522 : 58 = 9 (giây)
b) Thời gian để con chim chạm mặt đất là:
4182 : 82 = 51 (giây)
Đáp số: a) 9 giây
b) 51 giây
Loài động vật nhỏ chạy nhanh như thế nào?
Có một loài ve dài chỉ khoảng 0,7mm (bằng 1 hạt vừng) nhưng mỗi giây nó có thể chạy được quãng đường dài gấp 322 lần chiều dài cơ thể.
a) Tính vận tốc chạy của loài ve này.
b) Nếu di chuyển với vận tốc như vậy về phía trước trong 5 phút thì loài ve này đi được quãng đường bao xa?
Phương pháp giải:
a) Bước 2: Tính vận tốc = chiều dài của ve x 322
b) Bước 1: Đổi phút sang giây
Bước 2: Tính quãng đường ve chạy trong 5 phút = vận tốc x thời gian
Lời giải chi tiết:
a) Vận tốc của loài ve này là
0,7 x 322 = 225,4 (mm/giây)
b) Đổi 5 phút = 300 giây
Quãng đường ve chạy trong 5 phút là:
225,4 x 300 = 67 620 (mm)
Đáp số: a) 225,4 mm/giây
b) 67 620 mm
King’s Island là một trong các công viên nước được yêu thích nhất ở Mỹ. Công viên này gây ấn tượng với các đường tàu lượn ngoạn mục. Tàu lượn Banshee được ghi nhận có hành trình dài nhất thế giới: đi hết một vòng lượn có quãng đường dài 1257m với vận tốc lên đến 109km/giờ. Nếu đi với vận tốc 100km/giờ thì tàu lượn Banshee mất bao nhiêu thời gian để đi hết một vòng lượn?
Phương pháp giải:
Bước 1: Đổi mét sang ki-lô-mét
Bước 2: Thời gian để tàu lượn Banshee đi hết một vòng với vận tốc 100km/giờ = quãng đường : vận tốc
Lời giải chi tiết:
Đổi 1257 m = 1,257 km
Nếu đi với vận tốc 100km/giờ thì thời gian để tàu lượn Banshee đi hết một vòng là:
1,257 : 100 = 0,01257 ( giờ )
Đáp số: 0,01257 giờ
Một xe máy chạy từ tỉnh A, nếu chạy mỗi giờ 40km thì đến tỉnh B lúc 18 giờ. Nếu chạy mỗi giờ 30km thì đến tỉnh B lúc 18 giờ 30 phút. Tính quãng đường AB, biết xe không nghỉ trong lúc chạy.
Lời giải chi tiết:
Nếu xe máy chạy mỗi giờ 40km thì đến tỉnh B nhanh hơn chạy mỗi giờ 30km là:
18 giờ 30 phút – 18 giờ = 30 phút = 0,5 giờ
Gọi v1, t1 là vận tốc và thời gian đi với vận tốc 40km/giờ
v2, t2 là vận tốc và thời gian đi với vận tốc 30km/giờ
Trên cùng một quãng đường thì vận tốc và thời gian là 2 đại lượng tỉ lệ nghịch
Suy ra $\frac{{{v_1}}}{{{v_2}}} = \frac{{{t_2}}}{{{t_1}}} = \frac{{40}}{{30}} = \frac{4}{3}$
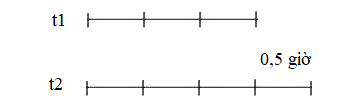
Thời gian khi đi 40km/giờ là:
t1 = 0,5 : (4 – 3) x 3 = 1,5 (giờ)
Quãng đường AB là:
40 x 1,5 = 60 (km)
Đáp số: 60km
Loài động vật nhỏ chạy nhanh như thế nào?
Có một loài ve dài chỉ khoảng 0,7mm (bằng 1 hạt vừng) nhưng mỗi giây nó có thể chạy được quãng đường dài gấp 322 lần chiều dài cơ thể.
a) Tính vận tốc chạy của loài ve này.
b) Nếu di chuyển với vận tốc như vậy về phía trước trong 5 phút thì loài ve này đi được quãng đường bao xa?
Phương pháp giải:
a) Bước 2: Tính vận tốc = chiều dài của ve x 322
b) Bước 1: Đổi phút sang giây
Bước 2: Tính quãng đường ve chạy trong 5 phút = vận tốc x thời gian
Lời giải chi tiết:
a) Vận tốc của loài ve này là
0,7 x 322 = 225,4 (mm/giây)
b) Đổi 5 phút = 300 giây
Quãng đường ve chạy trong 5 phút là:
225,4 x 300 = 67 620 (mm)
Đáp số: a) 225,4 mm/giây
b) 67 620 mm
Chúng ta thường được nghe câu thành ngữ "Nhanh như cắt". Vậy chim cắt nhanh đến mức nào?
Một con chim cắt Bắc Cực – loài chim săn mồi – có thể đạt đến vận tốc 58m/giây. Khi săn mồi, chim cắt có thể tìm đến vị trí rất cao sau đó lợi dụng trọng lực để lao xuống con mồi bên dưới.
a) Nếu lao từ độ cao 522m xuống mặt đất thì con chim này mất bao nhiêu thời gian?
b) Một thử nghiệm khác cho thấy chim cắt còn có thể đạt được tốc độ 82m/giây khi được thả từ độ cao 4182m. Tính thời gian con chim này chạm đến mặt đất khi được thả từ độ cao đó.
Phương pháp giải:
a) Tính thời gian để con chim lao xuống mặt đất = độ cao lao xuống : vận tốc
b) Tính thời gian để con chim chạm mặt đất = độ cao: tốc độ chim cắt đạt được
Lời giải chi tiết:
a) Thời gian để con chim lao xuống mặt đất là:
522 : 58 = 9 (giây)
b) Thời gian để con chim chạm mặt đất là:
4182 : 82 = 51 (giây)
Đáp số: a) 9 giây
b) 51 giây
Một xe máy chạy từ tỉnh A, nếu chạy mỗi giờ 40km thì đến tỉnh B lúc 18 giờ. Nếu chạy mỗi giờ 30km thì đến tỉnh B lúc 18 giờ 30 phút. Tính quãng đường AB, biết xe không nghỉ trong lúc chạy.
Lời giải chi tiết:
Nếu xe máy chạy mỗi giờ 40km thì đến tỉnh B nhanh hơn chạy mỗi giờ 30km là:
18 giờ 30 phút – 18 giờ = 30 phút = 0,5 giờ
Gọi v1, t1 là vận tốc và thời gian đi với vận tốc 40km/giờ
v2, t2 là vận tốc và thời gian đi với vận tốc 30km/giờ
Trên cùng một quãng đường thì vận tốc và thời gian là 2 đại lượng tỉ lệ nghịch
Suy ra $\frac{{{v_1}}}{{{v_2}}} = \frac{{{t_2}}}{{{t_1}}} = \frac{{40}}{{30}} = \frac{4}{3}$
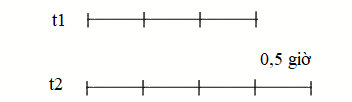
Thời gian khi đi 40km/giờ là:
t1 = 0,5 : (4 – 3) x 3 = 1,5 (giờ)
Quãng đường AB là:
40 x 1,5 = 60 (km)
Đáp số: 60km
King’s Island là một trong các công viên nước được yêu thích nhất ở Mỹ. Công viên này gây ấn tượng với các đường tàu lượn ngoạn mục. Tàu lượn Banshee được ghi nhận có hành trình dài nhất thế giới: đi hết một vòng lượn có quãng đường dài 1257m với vận tốc lên đến 109km/giờ. Nếu đi với vận tốc 100km/giờ thì tàu lượn Banshee mất bao nhiêu thời gian để đi hết một vòng lượn?
Phương pháp giải:
Bước 1: Đổi mét sang ki-lô-mét
Bước 2: Thời gian để tàu lượn Banshee đi hết một vòng với vận tốc 100km/giờ = quãng đường : vận tốc
Lời giải chi tiết:
Đổi 1257 m = 1,257 km
Nếu đi với vận tốc 100km/giờ thì thời gian để tàu lượn Banshee đi hết một vòng là:
1,257 : 100 = 0,01257 ( giờ )
Đáp số: 0,01257 giờ
Phần C của bài tập phát triển năng lực Toán 5 tập 2 trang 34 thường tập trung vào việc vận dụng kiến thức đã học để giải quyết các bài toán thực tế, đòi hỏi học sinh phải có khả năng phân tích, suy luận và tư duy logic. Các bài toán này không chỉ kiểm tra kiến thức mà còn đánh giá khả năng áp dụng kiến thức vào cuộc sống.
Thông thường, phần C trang 34 sẽ bao gồm các dạng bài tập sau:
Để giải tốt các bài tập phần C trang 34, học sinh cần nắm vững các phương pháp sau:
Bài toán: Một mảnh đất hình chữ nhật có chiều dài 20m, chiều rộng 15m. Người ta trồng rau trên mảnh đất đó, mỗi mét vuông thu hoạch được 5kg rau. Hỏi cả mảnh đất thu hoạch được bao nhiêu ki-lô-gam rau?
Giải:
Khi giải bài tập phần C trang 34, học sinh cần lưu ý những điều sau:
Việc giải bài tập phần C trang 34 không chỉ giúp học sinh củng cố kiến thức đã học mà còn rèn luyện kỹ năng giải quyết vấn đề, tư duy logic và khả năng áp dụng kiến thức vào thực tế. Đây là những kỹ năng quan trọng không chỉ trong học tập mà còn trong cuộc sống.
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp đầy đủ các bài giải chi tiết, dễ hiểu cho các bài tập trong sách giáo khoa và sách bài tập Toán 5 tập 2. Chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất, giúp các em học toán một cách hiệu quả và thú vị.
| Dạng bài tập | Mục tiêu |
|---|---|
| Số học | Vận dụng các phép tính, giải bài toán có nhiều bước |
| Hình học | Tính diện tích, chu vi, thể tích |
| Đại lượng và đơn vị đo | Đổi đơn vị, tính vận tốc, thời gian, quãng đường |
| Bài toán thực tế | Áp dụng kiến thức vào giải quyết tình huống |
Hy vọng với bài viết này, các em học sinh sẽ tự tin hơn khi giải các bài tập phần C. Vận dụng, phát triển trang 34 Bài tập phát triển năng lực Toán 5 tập 2. Chúc các em học tốt!