Chào mừng các em học sinh đến với bài giải chi tiết phần A. Tái hiện, củng cố trang 46 trong sách Bài tập phát triển năng lực Toán 5 tập 2. Bài học này giúp các em ôn lại kiến thức đã học và rèn luyện kỹ năng giải toán một cách hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em tự tin chinh phục các bài toán khó.
Tính bằng cách thuận tiện nhất: 55874 – 3593 – 5874 + 7593 Tính nhẩm: 0,125 x 17,81 x 800 = ....
Tính:
a) 12,3 : 10 = ..................................
24,6 : 100 = .................................
35,7 : 1000 = ...............................
1,23 : 0,1 = ..............................
2,46 : 0,01 = .............................
3,57 : 0,001 = ............................
b) 41 : 0,25 = ................................
41 x 4 = ................................
85 : 0,5 = ................................
85 x 2 = ...............................
Phương pháp giải:
- Muốn chia một số thập phân cho 0,1; 0,01; 0,001;.... ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên phải một, hai, ba, ... chữ số
- Muốn chia một số thập phân cho 10; 100; 1000; …. ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba,… chữ số.
- Muốn chia một số cho 0,5 ta chỉ việc nhân số đó với 2
- Muốn chia một số cho 0,25 ta chỉ việc nhân số đó với 4
Lời giải chi tiết:
a) 12,3 : 10 = 1,23
24,6 : 100 = 0,246
35,7 : 1000 = 0,0357
1,23 : 0,1 = 12,3
2,46 : 0,01 = 246
3,57 : 0,001 = 3570
b) 41 : 0,25 = 41 x 4 = 164
41 x 4 = 164
85 : 0,5 = 85 x 2 = 170
85 x 2 = 170
a) Đặt tính rồi tính:
21530 – 1709
9,197 – 2,537
45,8 – 37,74
b) Tính:
$\frac{4}{3} - \frac{5}{9}$
$\frac{2}{3} - \frac{2}{7}$
$2\frac{3}{5} - \frac{4}{{10}}$
Phương pháp giải:
a) Đặt tính sao cho các chữ số ở cùng một hàng thẳng cột với nhau. Thực hiện trừ lần lượt từ phải sang trái.
b) Muốn trừ hai phân số ta quy đồng mẫu số hai phân số rồi trừ hai phân số sau khi quy đồng.
Lời giải chi tiết:
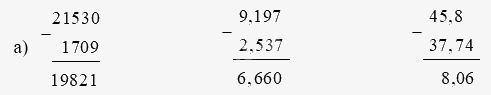
b) $\frac{4}{3} - \frac{5}{9}$ = $\frac{{24}}{{18}} - \frac{{10}}{{18}} = \frac{{14}}{{18}} = \frac{7}{9}$
$\frac{2}{3} - \frac{2}{7}$ = $\frac{{14}}{{21}} - \frac{6}{{21}} = \frac{8}{{21}}$
$2\frac{3}{5} - \frac{4}{{10}}$= $\frac{{13}}{5} - \frac{4}{{10}}$= $\frac{{26}}{{10}} - \frac{4}{{10}}$=$\frac{{22}}{{10}} = \frac{{11}}{5}$
a) Đặt tính rồi tính
5623 x 545
71,9 x 5
21,8 x 0,65
b) Tính:
$\frac{5}{7} \times \frac{{21}}{{25}}$
$\frac{{15}}{{75}} \times \frac{{40}}{{72}}$
$2\frac{1}{4} \times 3\frac{7}{3}$
Phương pháp giải:
a) Đặt tính rồi tính theo các quy tắc đã học
b) Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
Lời giải chi tiết:
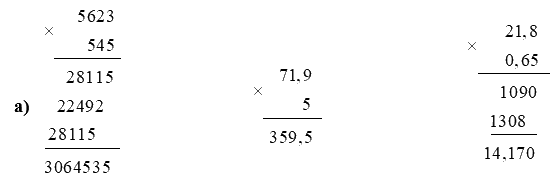
b)$\frac{5}{7} \times \frac{{21}}{{25}}$ = $\frac{{5 \times 7 \times 3}}{{7 \times 5 \times 5}} = \frac{3}{5}$
$\frac{{15}}{{75}} \times \frac{{40}}{{72}}$ = $\frac{{15 \times 8 \times 5}}{{5 \times 15 \times 8 \times 9}}$=$\frac{1}{9}$
$2\frac{1}{4} \times 3\frac{7}{3}$= $\frac{9}{4} \times \frac{{16}}{3}$=$\frac{{3 \times 3 \times 4 \times 4}}{{4 \times 3}}$= 12
a) Đặt tính rồi tính:
1620 : 12
592,8 : 13
125,8 : 1,25
b) Tính:
$\frac{4}{9}$: $\frac{{16}}{{27}}$
$\frac{{18}}{{81}}$ : $\frac{{150}}{{135}}$
$3\frac{5}{6}$ : $2\frac{2}{3}$
Phương pháp giải:
a) Đặt tính rồi tính theo quy tắc đã học.
b) Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Lời giải chi tiết:

b) $\frac{4}{9}$: $\frac{{16}}{{27}}$ = $\frac{4}{9} \times \frac{{27}}{{16}}$= $\frac{{4 \times 9 \times 3}}{{9 \times 4 \times 4}} = \frac{3}{4}$
$\frac{{18}}{{81}}$ : $\frac{{150}}{{135}}$ = $\frac{{18}}{{81}} \times \frac{{135}}{{150}} = \frac{2}{9} \times \frac{9}{{10}}$ = $\frac{{2 \times 9}}{{9 \times 2 \times 5}}$=$\frac{1}{5}$
$3\frac{5}{6}$ : $2\frac{2}{3}$ = $\frac{{23}}{6}:\frac{8}{3}$ = $\frac{{23}}{6}$ x $\frac{3}{8}$ = $\frac{{23 \times 3}}{{2 \times 3 \times 8}}$=$\frac{{23}}{{16}}$
a) Đặt tính rồi tính:
21530 – 1709
9,197 – 2,537
45,8 – 37,74
b) Tính:
$\frac{4}{3} - \frac{5}{9}$
$\frac{2}{3} - \frac{2}{7}$
$2\frac{3}{5} - \frac{4}{{10}}$
Phương pháp giải:
a) Đặt tính sao cho các chữ số ở cùng một hàng thẳng cột với nhau. Thực hiện trừ lần lượt từ phải sang trái.
b) Muốn trừ hai phân số ta quy đồng mẫu số hai phân số rồi trừ hai phân số sau khi quy đồng.
Lời giải chi tiết:
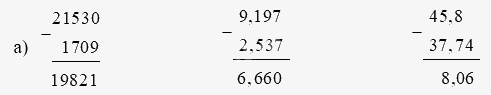
b) $\frac{4}{3} - \frac{5}{9}$ = $\frac{{24}}{{18}} - \frac{{10}}{{18}} = \frac{{14}}{{18}} = \frac{7}{9}$
$\frac{2}{3} - \frac{2}{7}$ = $\frac{{14}}{{21}} - \frac{6}{{21}} = \frac{8}{{21}}$
$2\frac{3}{5} - \frac{4}{{10}}$= $\frac{{13}}{5} - \frac{4}{{10}}$= $\frac{{26}}{{10}} - \frac{4}{{10}}$=$\frac{{22}}{{10}} = \frac{{11}}{5}$
a) Đặt tính rồi tính
5623 x 545
71,9 x 5
21,8 x 0,65
b) Tính:
$\frac{5}{7} \times \frac{{21}}{{25}}$
$\frac{{15}}{{75}} \times \frac{{40}}{{72}}$
$2\frac{1}{4} \times 3\frac{7}{3}$
Phương pháp giải:
a) Đặt tính rồi tính theo các quy tắc đã học
b) Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
Lời giải chi tiết:
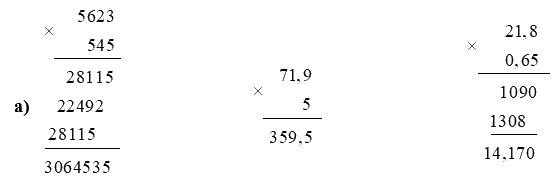
b)$\frac{5}{7} \times \frac{{21}}{{25}}$ = $\frac{{5 \times 7 \times 3}}{{7 \times 5 \times 5}} = \frac{3}{5}$
$\frac{{15}}{{75}} \times \frac{{40}}{{72}}$ = $\frac{{15 \times 8 \times 5}}{{5 \times 15 \times 8 \times 9}}$=$\frac{1}{9}$
$2\frac{1}{4} \times 3\frac{7}{3}$= $\frac{9}{4} \times \frac{{16}}{3}$=$\frac{{3 \times 3 \times 4 \times 4}}{{4 \times 3}}$= 12
Tính:
a) 12,3 : 10 = ..................................
24,6 : 100 = .................................
35,7 : 1000 = ...............................
1,23 : 0,1 = ..............................
2,46 : 0,01 = .............................
3,57 : 0,001 = ............................
b) 41 : 0,25 = ................................
41 x 4 = ................................
85 : 0,5 = ................................
85 x 2 = ...............................
Phương pháp giải:
- Muốn chia một số thập phân cho 0,1; 0,01; 0,001;.... ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên phải một, hai, ba, ... chữ số
- Muốn chia một số thập phân cho 10; 100; 1000; …. ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba,… chữ số.
- Muốn chia một số cho 0,5 ta chỉ việc nhân số đó với 2
- Muốn chia một số cho 0,25 ta chỉ việc nhân số đó với 4
Lời giải chi tiết:
a) 12,3 : 10 = 1,23
24,6 : 100 = 0,246
35,7 : 1000 = 0,0357
1,23 : 0,1 = 12,3
2,46 : 0,01 = 246
3,57 : 0,001 = 3570
b) 41 : 0,25 = 41 x 4 = 164
41 x 4 = 164
85 : 0,5 = 85 x 2 = 170
85 x 2 = 170
a) Đặt tính rồi tính:
1620 : 12
592,8 : 13
125,8 : 1,25
b) Tính:
$\frac{4}{9}$: $\frac{{16}}{{27}}$
$\frac{{18}}{{81}}$ : $\frac{{150}}{{135}}$
$3\frac{5}{6}$ : $2\frac{2}{3}$
Phương pháp giải:
a) Đặt tính rồi tính theo quy tắc đã học.
b) Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Lời giải chi tiết:
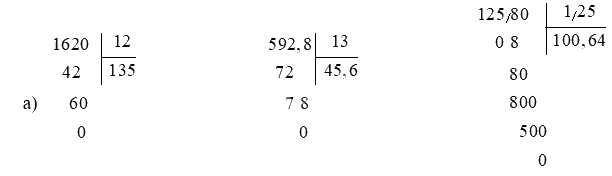
b) $\frac{4}{9}$: $\frac{{16}}{{27}}$ = $\frac{4}{9} \times \frac{{27}}{{16}}$= $\frac{{4 \times 9 \times 3}}{{9 \times 4 \times 4}} = \frac{3}{4}$
$\frac{{18}}{{81}}$ : $\frac{{150}}{{135}}$ = $\frac{{18}}{{81}} \times \frac{{135}}{{150}} = \frac{2}{9} \times \frac{9}{{10}}$ = $\frac{{2 \times 9}}{{9 \times 2 \times 5}}$=$\frac{1}{5}$
$3\frac{5}{6}$ : $2\frac{2}{3}$ = $\frac{{23}}{6}:\frac{8}{3}$ = $\frac{{23}}{6}$ x $\frac{3}{8}$ = $\frac{{23 \times 3}}{{2 \times 3 \times 8}}$=$\frac{{23}}{{16}}$
Phần A. Tái hiện, củng cố trang 46 trong sách Bài tập phát triển năng lực Toán 5 tập 2 tập trung vào việc giúp học sinh ôn tập và củng cố kiến thức về các phép tính cơ bản, các khái niệm hình học đã học. Các bài tập trong phần này thường mang tính ứng dụng cao, giúp học sinh rèn luyện kỹ năng giải quyết vấn đề thực tế.
Bài 1 yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia số thập phân. Để giải bài này, học sinh cần nắm vững các quy tắc về vị trí dấu phẩy, cách thực hiện các phép tính với số thập phân.
Giải: Thực hiện phép cộng như cộng số tự nhiên, sau đó đặt dấu phẩy sao cho số chữ số sau dấu phẩy ở tổng bằng số chữ số sau dấu phẩy ở các số hạng. Đáp án: 6,3
Giải: Thực hiện phép trừ như trừ số tự nhiên, sau đó đặt dấu phẩy. Đáp án: 5,3
Bài 2 yêu cầu học sinh tính diện tích của hình chữ nhật và hình vuông khi biết độ dài các cạnh. Công thức tính diện tích hình chữ nhật là: Diện tích = Chiều dài x Chiều rộng. Công thức tính diện tích hình vuông là: Diện tích = Cạnh x Cạnh.
Ví dụ: Một hình chữ nhật có chiều dài 8cm và chiều rộng 5cm. Tính diện tích của hình chữ nhật đó.
Giải: Diện tích = 8cm x 5cm = 40cm2. Đáp án: 40cm2
Bài 3 thường là một bài toán tổng hợp, yêu cầu học sinh vận dụng kiến thức về số thập phân và diện tích để giải quyết. Để giải bài này, học sinh cần đọc kỹ đề bài, xác định đúng các dữ kiện và công thức cần sử dụng.
Ví dụ: Một mảnh đất hình chữ nhật có chiều dài 15m và chiều rộng 8m. Người ta sử dụng 20% diện tích mảnh đất để trồng rau. Tính diện tích phần đất trồng rau.
Giải:
Đáp án: 24m2
Việc ôn tập và củng cố kiến thức là rất quan trọng trong quá trình học tập. Nó giúp học sinh nắm vững kiến thức đã học, rèn luyện kỹ năng giải toán và chuẩn bị tốt cho các bài kiểm tra, thi cử. giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp các bài giải chi tiết, dễ hiểu và các bài tập luyện tập đa dạng.
Ngoài sách Bài tập phát triển năng lực Toán 5 tập 2, các em có thể tham khảo thêm các tài liệu sau:
Chúc các em học tập tốt và đạt kết quả cao!