Chào mừng các em học sinh đến với bài trắc nghiệm Bài 4: Chu vi và diện tích của một số hình trong thực tiễn (tiếp) môn Toán 6, chương trình Chân trời sáng tạo. Bài trắc nghiệm này được thiết kế để giúp các em ôn luyện và củng cố kiến thức đã học về cách tính chu vi và diện tích của các hình quen thuộc trong thực tế.
Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm đa dạng, bám sát sách giáo khoa, giúp các em tự đánh giá năng lực và chuẩn bị tốt nhất cho các bài kiểm tra sắp tới.
Diện tích hình thang sau bằng:
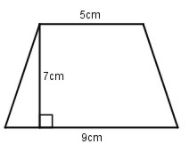
Một hình thang có diện tích 20 m2, đáy lớn 55dm và đáy bé 45dm. Tính chiều cao của hình thang?
Tính trung bình cộng hai đáy của một hình thang, biết rằng diện tích hình thang bằng 7m2 và chiều cao bằng 2m.
Một thửa ruộng hình thang có đáy bé 26m, đáy lớn hơn đáy bé 8m, đáy bé hơn chiều cao 6m. Trung bình cứ 100m2 thu hoạch được 70,5kg thóc. Hỏi thu hoạch được bao nhiêu ki-lô-gam thóc trên thửa ruộng đó?
Cho hình thang có độ dài hai cạnh bên là 5 cm và 7 cm, đáy lớn gấp đôi đáy nhỏ, biết độ dài đáy nhỏ là 6 cm. Chu vi hình thang là:
Diện tích hình thoi có độ dài hai đường chéo là 15cm và 6cm là:
Nếu hình thoi có độ dài 1 cạnh là a thì:
Một mảnh đất dạng hình thoi có độ dài đường chéo bé là 24m, độ dài đường chéo lớn gấp hai lần đường chéo bé. Diện tích của mảnh đất đó là:
Tính diện tích của hình thoi có tổng độ dài hai đường chéo là 30cm và đường chéo lớn hơn đường chéo bé 2cm.
110 cm2
Hình thoi A có độ dài hai đường chéo gấp đôi độ dài hai đường chéo của hình thoi B. Hỏi hình thoi A có diện tích gấp mấy lần diện tích hình thoi B?
Một hình thoi có diện tích 12dm2, độ dài một đường chéo là 3dm. Tính độ dài đường chéo thứ 2.
Một khu đất hình thoi có độ dài cạnh là 12 m. Người ta định xây tường rào xung quanh và bớt lại cửa ra vào rộng 1,5m. Hỏi người ta cần xây bao nhiêu mét tường rào?
Cho hình bình hành có diện tích là 312 m2, độ dài đáy là 24 m, chiều cao hình bình hành đó là:
Cho khu đất hình bình hành độ dài đáy là 300 dm, chiều cao khu đất hình bình hành là 20 m. Diện tích hình bình hành đó là:
6000 cm2
Chọn câu đúng:
Chọn câu đúng:
Chu vi hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
Cho hình bình hành có chu vi là 480cm, có độ dài cạnh đáy gấp 5 lần cạnh kia và gấp 8 lần chiều cao. Tính diện tích hình bình hành
Mảnh đất hình bình hành có cạnh đáy là 47 m, mở rộng mảnh đất bằng cách tăng các cạnh đáy của hình bình hành này thêm 7 m thì được mảnh đất hình bình hành mới có diện tích hơn diện tích mảnh đất ban đầu là 189 m2. Hãy tính diện tích mảnh đất ban đầu.
Cho hình bình hành ABCD có chiều cao hạ xuống cạnh CD là 5 cm, chiều dài CD là 15 cm, diện tích hình bình hành ABCD là:
Lời giải và đáp án
Diện tích hình thang sau bằng:
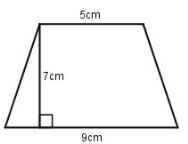
Đáp án : B
- Diện tích của hình thang bằng tổng độ dài hai đáy nhân với chiều cao rồi chia đôi.
\(S = \dfrac{{(a + b).h}}{2}\)
Diện tích hình thang đã cho là: \(\frac{{\left( {5 + 9} \right).7}}{2} = 49\,\,\left( {c{m^2}} \right)\)
Một hình thang có diện tích 20 m2, đáy lớn 55dm và đáy bé 45dm. Tính chiều cao của hình thang?
Đáp án : C
- Đổi các dữ kiện ra cùng đơn vị đo.
- Gọi đáy lớn, đáy nhỏ, chiều cao, diện tích của hình thang lần lượt là:\( a; b; h; S.\)
\(S = \dfrac{{(a + b).h}}{2} \Rightarrow h = 2.S:\left( {a + b} \right)\)
Đổi \(20\,{m^2} = 2000\,\,d{m^2}\)
Chiều cao của hình thang là:
\(2.2000:(55 + 45) = 40\,(dm)\)
Tính trung bình cộng hai đáy của một hình thang, biết rằng diện tích hình thang bằng 7m2 và chiều cao bằng 2m.
Đáp án : A
- Gọi đáy lớn, đáy nhỏ, chiều cao, diện tích của hình thang lần lượt là:\( a; b; h; S.\)
\(S = \dfrac{{(a + b).h}}{2} \Rightarrow \dfrac{{a + b}}{2} = S:h\)
Trung bình cộng hai đáy của hình thang là: \(7:2 = 3,5\) (m)
Một thửa ruộng hình thang có đáy bé 26m, đáy lớn hơn đáy bé 8m, đáy bé hơn chiều cao 6m. Trung bình cứ 100m2 thu hoạch được 70,5kg thóc. Hỏi thu hoạch được bao nhiêu ki-lô-gam thóc trên thửa ruộng đó?
Đáp án : A
- Tính: độ dài đáy lớn = độ dài đáy bé + 8
- Tính chiều cao ta lấy độ dài đáy bé trừ đi 5m.
- Tính diện tích thửa ruộng ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho 2.
- Tìm tỉ số giữa diện tích và 100m2.
- Tính số thóc thu được: diện tích gấp 100m2 bao nhiêu lần thì số thóc thu được gấp 70,5kg bấy nhiêu lần.
Đáy lớn của thửa ruộng hình thang là:
26 + 8 = 34 (m)
Chiều cao của thửa ruộng hình thang là:
26 – 6 = 20 (m)
Diện tích thửa ruộng hình thang là:
\(\dfrac{{\left( {34 + 26} \right).20}}{2} = 600\,\left( {{m^2}} \right)\)
600m2 gấp 6 lần 100m2
Số ki-lô-gam thóc thu hoạch được trên thửa ruộng đó:
6 . 70,5 = 423 (kg)
Cho hình thang có độ dài hai cạnh bên là 5 cm và 7 cm, đáy lớn gấp đôi đáy nhỏ, biết độ dài đáy nhỏ là 6 cm. Chu vi hình thang là:
Đáp án : C
- Tính độ dài đáy lớn.
- Chu vi của hình thang bằng tổng độ dài các cạnh của hình thang đó.
Độ dài đáy lớn là: \(6.2 = 12\) (cm)
Chu vi hình thang là: \(5 + 7 + 6 + 12 = 30\) (cm)
Diện tích hình thoi có độ dài hai đường chéo là 15cm và 6cm là:
Đáp án : C
Diện tích hình thoi bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\)
Diện tích hình thoi là: \(S = \frac{{15.6}}{2} = 45\,\,\left( {c{m^2}} \right)\).
Nếu hình thoi có độ dài 1 cạnh là a thì:
Đáp án : A
Nếu hình thoi có độ dài 1 cạnh là a thì chu vi của hình thoi là 4a.
Một mảnh đất dạng hình thoi có độ dài đường chéo bé là 24m, độ dài đường chéo lớn gấp hai lần đường chéo bé. Diện tích của mảnh đất đó là:
Đáp án : A
- Tính độ dài đường chéo lớn
- Diện tích hình thoi bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\).
- Độ dài đường chéo lớn là: \(24.2 = 48\,\,\left( m \right)\)
=> Diện tích hình thoi là: \(\frac{{24.48}}{2} = 576\,\left( {{m^2}} \right)\)
Tính diện tích của hình thoi có tổng độ dài hai đường chéo là 30cm và đường chéo lớn hơn đường chéo bé 2cm.
110 cm2
Đáp án : B
- Độ dài đường chéo lớn = (Tổng độ dài hai đường chéo + Hiệu độ dài hai đường chéo) : 2
=> Độ dài đường chéo bé = Tổng độ dài hai đường chéo - Độ dài đường chéo lớn
- Diện tích hình thoi bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\).
Độ dài đường chéo lớn là: \(\left( {30 + 2} \right):2 = 16\,\left( {cm} \right)\)
Độ dài đường chéo bé là: \(30 - 16 = 14\left( {cm} \right)\)
Diện tích hình thoi là: \(\frac{{16.14}}{2} = 112\left( {c{m^2}} \right)\)
Hình thoi A có độ dài hai đường chéo gấp đôi độ dài hai đường chéo của hình thoi B. Hỏi hình thoi A có diện tích gấp mấy lần diện tích hình thoi B?
Đáp án : C
- Tính diện tích của hai hình thoi A và B dựa vào công thức:
Diện tích hình thoi bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\).
=> Từ đó kết luận.
Gọi độ dài hai đường chéo của hình thoi B lần lượt là m, n.
=> Độ dài hai đường chéo của hình thoi A lần lượt là 2m, 2n.
Diện tích của hình thoi A là: \(\frac{{2m.2n}}{2} = 2mn\)
Diện tích của hình thoi B là: \(\frac{{m.n}}{2}\)
Vậy hình thoi A có diện tích gấp 4 lần diện tích hình thoi B.
Một hình thoi có diện tích 12dm2, độ dài một đường chéo là 3dm. Tính độ dài đường chéo thứ 2.
Đáp án : C
Độ dài đường chéo thứ 2 = 2.Diện tích hình thoi : Độ dài đường chéo thứ nhất
Độ dài đường chéo thứ 2 là: \(2.12:3 = 8\,\,\left( {dm} \right)\)
Một khu đất hình thoi có độ dài cạnh là 12 m. Người ta định xây tường rào xung quanh và bớt lại cửa ra vào rộng 1,5m. Hỏi người ta cần xây bao nhiêu mét tường rào?
Đáp án : D
- Tính chu vi khu đất hình thoi
- Số mét tường rào phải xây = Chu vi – Độ rộng của ra vào
- Chu vi hình thoi là: \(12.4 = 48\,\,\left( m \right)\)
- Số mét tường phải xây là: \(48 - 1,5 = 46,5\,\,\left( m \right)\)
Cho hình bình hành có diện tích là 312 m2, độ dài đáy là 24 m, chiều cao hình bình hành đó là:
Đáp án : D
Chiều cao hình bình hành = Diện tích : Độ dài cạnh đáy
Hình bình hành đã cho có diện tích là 312 m2 và độ dài đáy là 24 m nên:
Chiều cao hình bình hành là: 312 : 24 = 13 (m)
Cho khu đất hình bình hành độ dài đáy là 300 dm, chiều cao khu đất hình bình hành là 20 m. Diện tích hình bình hành đó là:
6000 cm2
Đáp án : D
- Đổi các độ dài ra cùng đơn vị đo
- Tính diện tích hình bình hành
Diện tích hình bình hành là: \(S = b.h\)
Trong đó \(b\) là cạnh, \(h\) là chiều cao tương ứng.
Đổi 300 dm = 30 m
Diện tích hình bình hành đã cho là: 30 . 20 = 600 (m2)
Chọn câu đúng:
Đáp án : C
Diện tích hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
Chọn câu đúng:
Chu vi hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
Đáp án : D
Sử dụng công thức tính chu vi hình bình hành.
Chu vi của một hình bình hành bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ.
Cho hình bình hành có chu vi là 480cm, có độ dài cạnh đáy gấp 5 lần cạnh kia và gấp 8 lần chiều cao. Tính diện tích hình bình hành
Đáp án : D
- Tính nửa chu vi hình bình hành
- Tính cạnh đáy của hình bình hành
- Tính chiều cao của hình bình hành
=> Diện tích hình bình hành
Diện tích hình bình hành là: \(S = b.h\)
Trong đó \(b\) là cạnh, \(h\) là chiều cao tương ứng.
- Ta có nửa chu vi hình bình hành là: 480 : 2 = 240 (cm)
Cạnh đáy gấp 5 lần cạnh kia nên nửa chu vi sẽ gấp 6 lần cạnh kia.
- Ta có cạnh đáy hình bình hành là: 240 : 6 . 5 = 200 (cm)
- Chiều cao của hình bình hành là: 200 : 8 = 25 (cm)
- Diện tích của hình bình hành là: 200 . 25 = 5000 (cm2)
Mảnh đất hình bình hành có cạnh đáy là 47 m, mở rộng mảnh đất bằng cách tăng các cạnh đáy của hình bình hành này thêm 7 m thì được mảnh đất hình bình hành mới có diện tích hơn diện tích mảnh đất ban đầu là 189 m2. Hãy tính diện tích mảnh đất ban đầu.
Đáp án : D
Phần diện tích tăng thêm chính là diện tích hình bình hành có cạnh đáy 7m và chiều cao là chiều cao của mảnh đất hình bình hành ban đầu.
- Tính chiều cao của mảnh đất hình bình hành:
Chiều cao = Diện tích : Cạnh đáy
- Tính diện tích mảnh đất ban đầu:
Diện tích = Cạnh đáy . Chiều cao.
Phần diện tích tăng thêm chính là diện tích hình bình hành có cạnh đáy 7m và chiều cao là chiều cao của mảnh đất hình bình hành ban đầu.
Chiều cao mảnh đất là: 189 : 7 = 27 (m)
Diện tích mảnh đất hình bình hành ban đầu là: 27 . 47 = 1269 (m2)
Cho hình bình hành ABCD có chiều cao hạ xuống cạnh CD là 5 cm, chiều dài CD là 15 cm, diện tích hình bình hành ABCD là:
Đáp án : D
Diện tích hình bình hành là: \(S = b.h\)
Trong đó \(b\) là cạnh, \(h\) là chiều cao tương ứng.
Hình bình hành ABCD có chiều cao bằng 5 cm và độ dài cạnh đáy bằng 15 cm nên:
Diện tích hình bình hành ABCD là: 5 . 15 = 75 cm2
Diện tích hình thang sau bằng:

Một hình thang có diện tích 20 m2, đáy lớn 55dm và đáy bé 45dm. Tính chiều cao của hình thang?
Tính trung bình cộng hai đáy của một hình thang, biết rằng diện tích hình thang bằng 7m2 và chiều cao bằng 2m.
Một thửa ruộng hình thang có đáy bé 26m, đáy lớn hơn đáy bé 8m, đáy bé hơn chiều cao 6m. Trung bình cứ 100m2 thu hoạch được 70,5kg thóc. Hỏi thu hoạch được bao nhiêu ki-lô-gam thóc trên thửa ruộng đó?
Cho hình thang có độ dài hai cạnh bên là 5 cm và 7 cm, đáy lớn gấp đôi đáy nhỏ, biết độ dài đáy nhỏ là 6 cm. Chu vi hình thang là:
Diện tích hình thoi có độ dài hai đường chéo là 15cm và 6cm là:
Nếu hình thoi có độ dài 1 cạnh là a thì:
Một mảnh đất dạng hình thoi có độ dài đường chéo bé là 24m, độ dài đường chéo lớn gấp hai lần đường chéo bé. Diện tích của mảnh đất đó là:
Tính diện tích của hình thoi có tổng độ dài hai đường chéo là 30cm và đường chéo lớn hơn đường chéo bé 2cm.
110 cm2
Hình thoi A có độ dài hai đường chéo gấp đôi độ dài hai đường chéo của hình thoi B. Hỏi hình thoi A có diện tích gấp mấy lần diện tích hình thoi B?
Một hình thoi có diện tích 12dm2, độ dài một đường chéo là 3dm. Tính độ dài đường chéo thứ 2.
Một khu đất hình thoi có độ dài cạnh là 12 m. Người ta định xây tường rào xung quanh và bớt lại cửa ra vào rộng 1,5m. Hỏi người ta cần xây bao nhiêu mét tường rào?
Cho hình bình hành có diện tích là 312 m2, độ dài đáy là 24 m, chiều cao hình bình hành đó là:
Cho khu đất hình bình hành độ dài đáy là 300 dm, chiều cao khu đất hình bình hành là 20 m. Diện tích hình bình hành đó là:
6000 cm2
Chọn câu đúng:
Chọn câu đúng:
Chu vi hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
Cho hình bình hành có chu vi là 480cm, có độ dài cạnh đáy gấp 5 lần cạnh kia và gấp 8 lần chiều cao. Tính diện tích hình bình hành
Mảnh đất hình bình hành có cạnh đáy là 47 m, mở rộng mảnh đất bằng cách tăng các cạnh đáy của hình bình hành này thêm 7 m thì được mảnh đất hình bình hành mới có diện tích hơn diện tích mảnh đất ban đầu là 189 m2. Hãy tính diện tích mảnh đất ban đầu.
Cho hình bình hành ABCD có chiều cao hạ xuống cạnh CD là 5 cm, chiều dài CD là 15 cm, diện tích hình bình hành ABCD là:
Diện tích hình thang sau bằng:

Đáp án : B
- Diện tích của hình thang bằng tổng độ dài hai đáy nhân với chiều cao rồi chia đôi.
\(S = \dfrac{{(a + b).h}}{2}\)
Diện tích hình thang đã cho là: \(\frac{{\left( {5 + 9} \right).7}}{2} = 49\,\,\left( {c{m^2}} \right)\)
Một hình thang có diện tích 20 m2, đáy lớn 55dm và đáy bé 45dm. Tính chiều cao của hình thang?
Đáp án : C
- Đổi các dữ kiện ra cùng đơn vị đo.
- Gọi đáy lớn, đáy nhỏ, chiều cao, diện tích của hình thang lần lượt là:\( a; b; h; S.\)
\(S = \dfrac{{(a + b).h}}{2} \Rightarrow h = 2.S:\left( {a + b} \right)\)
Đổi \(20\,{m^2} = 2000\,\,d{m^2}\)
Chiều cao của hình thang là:
\(2.2000:(55 + 45) = 40\,(dm)\)
Tính trung bình cộng hai đáy của một hình thang, biết rằng diện tích hình thang bằng 7m2 và chiều cao bằng 2m.
Đáp án : A
- Gọi đáy lớn, đáy nhỏ, chiều cao, diện tích của hình thang lần lượt là:\( a; b; h; S.\)
\(S = \dfrac{{(a + b).h}}{2} \Rightarrow \dfrac{{a + b}}{2} = S:h\)
Trung bình cộng hai đáy của hình thang là: \(7:2 = 3,5\) (m)
Một thửa ruộng hình thang có đáy bé 26m, đáy lớn hơn đáy bé 8m, đáy bé hơn chiều cao 6m. Trung bình cứ 100m2 thu hoạch được 70,5kg thóc. Hỏi thu hoạch được bao nhiêu ki-lô-gam thóc trên thửa ruộng đó?
Đáp án : A
- Tính: độ dài đáy lớn = độ dài đáy bé + 8
- Tính chiều cao ta lấy độ dài đáy bé trừ đi 5m.
- Tính diện tích thửa ruộng ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho 2.
- Tìm tỉ số giữa diện tích và 100m2.
- Tính số thóc thu được: diện tích gấp 100m2 bao nhiêu lần thì số thóc thu được gấp 70,5kg bấy nhiêu lần.
Đáy lớn của thửa ruộng hình thang là:
26 + 8 = 34 (m)
Chiều cao của thửa ruộng hình thang là:
26 – 6 = 20 (m)
Diện tích thửa ruộng hình thang là:
\(\dfrac{{\left( {34 + 26} \right).20}}{2} = 600\,\left( {{m^2}} \right)\)
600m2 gấp 6 lần 100m2
Số ki-lô-gam thóc thu hoạch được trên thửa ruộng đó:
6 . 70,5 = 423 (kg)
Cho hình thang có độ dài hai cạnh bên là 5 cm và 7 cm, đáy lớn gấp đôi đáy nhỏ, biết độ dài đáy nhỏ là 6 cm. Chu vi hình thang là:
Đáp án : C
- Tính độ dài đáy lớn.
- Chu vi của hình thang bằng tổng độ dài các cạnh của hình thang đó.
Độ dài đáy lớn là: \(6.2 = 12\) (cm)
Chu vi hình thang là: \(5 + 7 + 6 + 12 = 30\) (cm)
Diện tích hình thoi có độ dài hai đường chéo là 15cm và 6cm là:
Đáp án : C
Diện tích hình thoi bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\)
Diện tích hình thoi là: \(S = \frac{{15.6}}{2} = 45\,\,\left( {c{m^2}} \right)\).
Nếu hình thoi có độ dài 1 cạnh là a thì:
Đáp án : A
Nếu hình thoi có độ dài 1 cạnh là a thì chu vi của hình thoi là 4a.
Một mảnh đất dạng hình thoi có độ dài đường chéo bé là 24m, độ dài đường chéo lớn gấp hai lần đường chéo bé. Diện tích của mảnh đất đó là:
Đáp án : A
- Tính độ dài đường chéo lớn
- Diện tích hình thoi bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\).
- Độ dài đường chéo lớn là: \(24.2 = 48\,\,\left( m \right)\)
=> Diện tích hình thoi là: \(\frac{{24.48}}{2} = 576\,\left( {{m^2}} \right)\)
Tính diện tích của hình thoi có tổng độ dài hai đường chéo là 30cm và đường chéo lớn hơn đường chéo bé 2cm.
110 cm2
Đáp án : B
- Độ dài đường chéo lớn = (Tổng độ dài hai đường chéo + Hiệu độ dài hai đường chéo) : 2
=> Độ dài đường chéo bé = Tổng độ dài hai đường chéo - Độ dài đường chéo lớn
- Diện tích hình thoi bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\).
Độ dài đường chéo lớn là: \(\left( {30 + 2} \right):2 = 16\,\left( {cm} \right)\)
Độ dài đường chéo bé là: \(30 - 16 = 14\left( {cm} \right)\)
Diện tích hình thoi là: \(\frac{{16.14}}{2} = 112\left( {c{m^2}} \right)\)
Hình thoi A có độ dài hai đường chéo gấp đôi độ dài hai đường chéo của hình thoi B. Hỏi hình thoi A có diện tích gấp mấy lần diện tích hình thoi B?
Đáp án : C
- Tính diện tích của hai hình thoi A và B dựa vào công thức:
Diện tích hình thoi bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\).
=> Từ đó kết luận.
Gọi độ dài hai đường chéo của hình thoi B lần lượt là m, n.
=> Độ dài hai đường chéo của hình thoi A lần lượt là 2m, 2n.
Diện tích của hình thoi A là: \(\frac{{2m.2n}}{2} = 2mn\)
Diện tích của hình thoi B là: \(\frac{{m.n}}{2}\)
Vậy hình thoi A có diện tích gấp 4 lần diện tích hình thoi B.
Một hình thoi có diện tích 12dm2, độ dài một đường chéo là 3dm. Tính độ dài đường chéo thứ 2.
Đáp án : C
Độ dài đường chéo thứ 2 = 2.Diện tích hình thoi : Độ dài đường chéo thứ nhất
Độ dài đường chéo thứ 2 là: \(2.12:3 = 8\,\,\left( {dm} \right)\)
Một khu đất hình thoi có độ dài cạnh là 12 m. Người ta định xây tường rào xung quanh và bớt lại cửa ra vào rộng 1,5m. Hỏi người ta cần xây bao nhiêu mét tường rào?
Đáp án : D
- Tính chu vi khu đất hình thoi
- Số mét tường rào phải xây = Chu vi – Độ rộng của ra vào
- Chu vi hình thoi là: \(12.4 = 48\,\,\left( m \right)\)
- Số mét tường phải xây là: \(48 - 1,5 = 46,5\,\,\left( m \right)\)
Cho hình bình hành có diện tích là 312 m2, độ dài đáy là 24 m, chiều cao hình bình hành đó là:
Đáp án : D
Chiều cao hình bình hành = Diện tích : Độ dài cạnh đáy
Hình bình hành đã cho có diện tích là 312 m2 và độ dài đáy là 24 m nên:
Chiều cao hình bình hành là: 312 : 24 = 13 (m)
Cho khu đất hình bình hành độ dài đáy là 300 dm, chiều cao khu đất hình bình hành là 20 m. Diện tích hình bình hành đó là:
6000 cm2
Đáp án : D
- Đổi các độ dài ra cùng đơn vị đo
- Tính diện tích hình bình hành
Diện tích hình bình hành là: \(S = b.h\)
Trong đó \(b\) là cạnh, \(h\) là chiều cao tương ứng.
Đổi 300 dm = 30 m
Diện tích hình bình hành đã cho là: 30 . 20 = 600 (m2)
Chọn câu đúng:
Đáp án : C
Diện tích hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
Chọn câu đúng:
Chu vi hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
Đáp án : D
Sử dụng công thức tính chu vi hình bình hành.
Chu vi của một hình bình hành bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ.
Cho hình bình hành có chu vi là 480cm, có độ dài cạnh đáy gấp 5 lần cạnh kia và gấp 8 lần chiều cao. Tính diện tích hình bình hành
Đáp án : D
- Tính nửa chu vi hình bình hành
- Tính cạnh đáy của hình bình hành
- Tính chiều cao của hình bình hành
=> Diện tích hình bình hành
Diện tích hình bình hành là: \(S = b.h\)
Trong đó \(b\) là cạnh, \(h\) là chiều cao tương ứng.
- Ta có nửa chu vi hình bình hành là: 480 : 2 = 240 (cm)
Cạnh đáy gấp 5 lần cạnh kia nên nửa chu vi sẽ gấp 6 lần cạnh kia.
- Ta có cạnh đáy hình bình hành là: 240 : 6 . 5 = 200 (cm)
- Chiều cao của hình bình hành là: 200 : 8 = 25 (cm)
- Diện tích của hình bình hành là: 200 . 25 = 5000 (cm2)
Mảnh đất hình bình hành có cạnh đáy là 47 m, mở rộng mảnh đất bằng cách tăng các cạnh đáy của hình bình hành này thêm 7 m thì được mảnh đất hình bình hành mới có diện tích hơn diện tích mảnh đất ban đầu là 189 m2. Hãy tính diện tích mảnh đất ban đầu.
Đáp án : D
Phần diện tích tăng thêm chính là diện tích hình bình hành có cạnh đáy 7m và chiều cao là chiều cao của mảnh đất hình bình hành ban đầu.
- Tính chiều cao của mảnh đất hình bình hành:
Chiều cao = Diện tích : Cạnh đáy
- Tính diện tích mảnh đất ban đầu:
Diện tích = Cạnh đáy . Chiều cao.
Phần diện tích tăng thêm chính là diện tích hình bình hành có cạnh đáy 7m và chiều cao là chiều cao của mảnh đất hình bình hành ban đầu.
Chiều cao mảnh đất là: 189 : 7 = 27 (m)
Diện tích mảnh đất hình bình hành ban đầu là: 27 . 47 = 1269 (m2)
Cho hình bình hành ABCD có chiều cao hạ xuống cạnh CD là 5 cm, chiều dài CD là 15 cm, diện tích hình bình hành ABCD là:
Đáp án : D
Diện tích hình bình hành là: \(S = b.h\)
Trong đó \(b\) là cạnh, \(h\) là chiều cao tương ứng.
Hình bình hành ABCD có chiều cao bằng 5 cm và độ dài cạnh đáy bằng 15 cm nên:
Diện tích hình bình hành ABCD là: 5 . 15 = 75 cm2
Bài 4 trong chương trình Toán 6 Chân trời sáng tạo tiếp tục đi sâu vào ứng dụng thực tế của việc tính chu vi và diện tích các hình. Không chỉ dừng lại ở các hình vuông, chữ nhật đơn giản, bài học này mở rộng ra các hình phức tạp hơn, đòi hỏi học sinh phải vận dụng linh hoạt các công thức và kỹ năng đã học để giải quyết vấn đề.
Để tính chu vi hình chữ nhật, ta sử dụng công thức: P = 2(a + b), trong đó a và b là chiều dài và chiều rộng của hình chữ nhật. Để tính diện tích hình chữ nhật, ta sử dụng công thức: S = a * b.
Ví dụ: Một hình chữ nhật có chiều dài 8cm và chiều rộng 5cm. Tính chu vi và diện tích của hình chữ nhật đó.
Giải:
Chu vi hình vuông được tính bằng công thức: P = 4a, trong đó a là độ dài một cạnh của hình vuông. Diện tích hình vuông được tính bằng công thức: S = a2.
Ví dụ: Một hình vuông có cạnh dài 6cm. Tính chu vi và diện tích của hình vuông đó.
Giải:
Trong các bài tập ứng dụng thực tế, cần đọc kỹ đề bài, xác định đúng hình dạng và các thông số liên quan. Sau đó, áp dụng các công thức phù hợp để giải quyết bài toán.
Ví dụ: Một mảnh đất hình chữ nhật có chiều dài 15m và chiều rộng 10m. Người ta muốn xây một hàng rào xung quanh mảnh đất đó. Hỏi cần bao nhiêu mét rào?
Giải:
Chu vi mảnh đất là: P = 2(15 + 10) = 50m. Vậy cần 50 mét rào để xây hàng rào xung quanh mảnh đất.
Trắc nghiệm Bài 4: Chu vi và diện tích của một số hình trong thực tiễn (tiếp) Toán 6 Chân trời sáng tạo là một phần quan trọng trong chương trình học. Việc nắm vững kiến thức và kỹ năng liên quan đến bài học này sẽ giúp các em giải quyết tốt các bài toán thực tế và đạt kết quả cao trong các kỳ thi.