Chào mừng các em học sinh đến với chuyên mục luyện tập Trắc nghiệm Bài tập ôn tập chương 8: Hình học phẳng. Các hình hình học cơ bản Toán 6 Chân trời sáng tạo của giaitoan.edu.vn. Chương này giúp các em củng cố kiến thức về các khái niệm cơ bản trong hình học phẳng.
Với bộ đề trắc nghiệm được thiết kế khoa học, các em sẽ có cơ hội tự đánh giá năng lực và rèn luyện kỹ năng giải bài tập một cách hiệu quả.
Có bao nhiêu đường thẳng đi qua hai điểm phân biệt A và B?
\(1\)
\(2\)
\(3\)
Vô số
Cho hình vẽ. Em hãy chọn đáp án đúng.

A nằm giữa hai điểm B và C
B nằm giữa hai điểm A và C
C nằm giữa hai điểm A và B
Không có điểm nào nằm giữa hai điểm còn lại
Cho điểm M nằm giữa điểm N và P như hình vẽ. Kết luận nào sau đây là đúng ?

Tia NM trùng với tia MP
Tia MP trùng với tia NP
Tia PM trùng với tia PN
Tia MN trùng với tia MP.
Cho hình vẽ:

Hình vẽ trên có bao nhiêu tia chung gốc B:
$5$
$3$
$4$
$2$
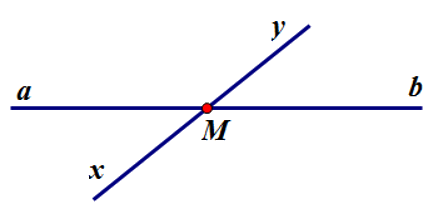
Cho hình vẽ sau. Chọn câu đúng.
Điểm M thuộc đường thẳng xy nhưng không thuộc đường thẳng ab
Hai đường thẳng xy và ab không có điểm chung
Đường thẳng xy cắt đường thẳng ab tại M
Đường thẳng xy và ab có hai điểm chung
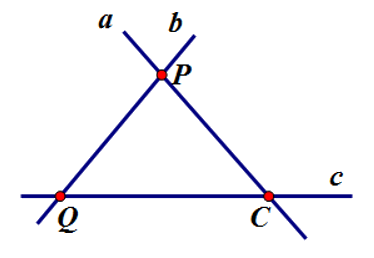
Cho hình vẽ sau. Chọn câu đúng.
\(P \in a;P \in c\)
\(Q \in b;Q \in c\)
Đường thẳng a cắt đường thẳng c tại điểm P
Không có hai đường thẳng nào cắt nhau trên hình vẽ
Cho hai tia Ox và Oy đối nhau. Lấy điểm G trên tia Ox, điểm H trên tia Oy. Ta có:
Điểm G nằm giữa hai điểm O và H
Điểm O nằm giữa hai điểm G và H
Điểm H nằm giữa hai điểm O và G
Không có điểm nào nằm giữa hai điểm còn lại
Vẽ ba đường thẳng phân biệt bất kì, số giao điểm của ba đường thẳng đó không thể là:
$0$
$1$ hoặc $2$
$4$
$3$
Cho hình vẽ. Em hãy chọn khẳng định sai:

NM và NI là hai tia đối nhau
IN và IM là hai tia trùng nhau
MN và MI là hai tia trùng nhau
MN và NI là hai tia trùng nhau
Cho L là điểm nằm giữa hai điểm I và K. Biết $IL = 2cm,{\rm{ }}LK = 5cm.$ Độ dài của đoạn thẳng IK là:
$3cm$
$2cm$
$5cm$
$7cm$
Cho đoạn thẳng $BC = 32cm.$ Gọi G là trung điểm của đoạn thẳng $BC,{\rm{ }}H$ là trung điểm của đoạn thẳng $GC.$ Khi đó, độ dài của đoạn thẳng BH là
$8cm$
$16cm$
$24cm$
$28cm$
Biết $IL = 4cm;{\rm{ }}LK = 5cm$ điều kiện để điểm I nằm giữa hai điểm L và K là:
\(IK=1cm\)
\(IK=9cm\)
\(IK=2cm\)
\(IK=3cm\)
Biết $IL = 4cm;{\rm{ }}LK = 5cm$ điều kiện để điểm I nằm giữa hai điểm L và K là:
\(IK=1cm\)
\(IK=9cm\)
\(IK=2cm\)
\(IK=3cm\)
Cho điểm I thuộc đoạn thẳng AB. Biết $AI = 5cm,AB = 8cm.$ Tính độ dài $BI.$
\(4cm\)
\(5cm\)
\(2cm\)
\(3cm\)
Lấy năm điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng. Cứ qua hai điểm ta vẽ một đường thẳng. Số đường thẳng có thể vẽ được là:
$3$
$10$
$12$
$4$
Cho trước 6 điểm trong đó có 4 điểm thẳng hàng. Vẽ các đoạn thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đoạn thẳng?
$15$
$16$
$14$
$13$
Cho 24 điểm trong đó có 6 điểm thẳng hàng. Qua 2 điểm ta kẻ được một đường thẳng. Hỏi kẻ được tất cả bao nhiêu đường thẳng?
\(276\)
\(290\)
\(262\)
\(226\)
Cho M thuộc đoạn thẳng AB, $AM = 4cm,{\rm{ }}AB = 6cm.$ Gọi O là trung điểm của đoạn AB.
Tính $MO$.
\(MO = 4cm\)
\(MO = 3cm\)
\(MO = 1cm\)
\(MO = 2cm\)
Trên AB lấy điểm I sao cho AI = 3,5cm. Lấy điểm P là trung điểm của AO. Chọn câu đúng.
Điểm I là trung điểm của OM
Điểm O nằm giữa I và P
\(IP = 2cm\)
Cả A, B, C đều đúng.
Lời giải và đáp án
Có bao nhiêu đường thẳng đi qua hai điểm phân biệt A và B?
\(1\)
\(2\)
\(3\)
Vô số
Đáp án : A
Có 1 và chỉ 1 đường thẳng đi qua 2 điểm phân biệt cho trước.
Có 1 và chỉ 1 đường thẳng đi qua 2 điểm phân biệt cho trước. Vậy có duy nhất 1 đường thẳng đi qua hai điểm A và B.
Cho hình vẽ. Em hãy chọn đáp án đúng.

A nằm giữa hai điểm B và C
B nằm giữa hai điểm A và C
C nằm giữa hai điểm A và B
Không có điểm nào nằm giữa hai điểm còn lại
Đáp án : B
Quan sát hình vẽ và xác định điểm nằm giữa hai điểm còn lại
Quan sát hình vẽ ta thấy điểm B nằm giữa hai điểm A và C.
Cho điểm M nằm giữa điểm N và P như hình vẽ. Kết luận nào sau đây là đúng ?

Tia NM trùng với tia MP
Tia MP trùng với tia NP
Tia PM trùng với tia PN
Tia MN trùng với tia MP.
Đáp án : C
Hai tia trùng nhau là hai tia chung gốc và tạo thành nửa đường thẳng.
Nhận xét:
+ Đáp án A: Hai tia NM và MP là hai tia không chung gốc nên loại đáp án A.
+ Đáp án B: Hai tia MP và NP là hai tia không chung gốc nên loại đáp án B.
+ Đáp án C: thấy hai tia PN và PM là hai tia cùng chung gốc P và tạo thành nửa đường thẳng nên hai tia PN và PM là hai tia trùng nhau, do đó chọn đáp án C.
+ Đáp án D: Hai tia MN và MP là hai tia chung gốc nhưng tạo thành một đường thẳng nên hai tia MN và MP là hai tia đối nhau, do đó loại đáp án D.
Cho hình vẽ:

Hình vẽ trên có bao nhiêu tia chung gốc B:
$5$
$3$
$4$
$2$
Đáp án : A
Ta liệt kê tất cả các tia chung gốc B, kể cả các tia trùng nhau.

Hình vẽ trên có các tia chung gốc B là: BA, Bx, By, BC và BD. Vậy có tất cả 5 tia chung gốc B.
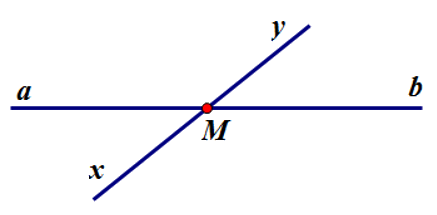
Cho hình vẽ sau. Chọn câu đúng.
Điểm M thuộc đường thẳng xy nhưng không thuộc đường thẳng ab
Hai đường thẳng xy và ab không có điểm chung
Đường thẳng xy cắt đường thẳng ab tại M
Đường thẳng xy và ab có hai điểm chung
Đáp án : C
Quan sát hình vẽ và sử dụng kiến thức về điểm, đường thẳng
Ta thấy hai đường thẳng xy và ab cắt nhau tại M nên đáp án C đúng.
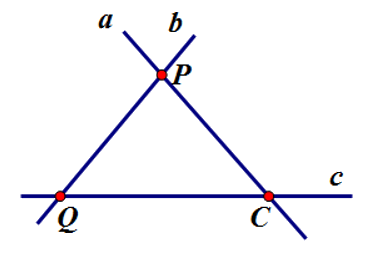
Cho hình vẽ sau. Chọn câu đúng.
\(P \in a;P \in c\)
\(Q \in b;Q \in c\)
Đường thẳng a cắt đường thẳng c tại điểm P
Không có hai đường thẳng nào cắt nhau trên hình vẽ
Đáp án : B
Quan sát hình vẽ và sử dụng kiến thức về điểm và đường thẳng
Từ hình vẽ ta thấy \(P \in a;P \in c\) nên đáp án A sai; \(Q \in b;Q \in c\) nên đáp án B đúng.
Hai đường thẳng a và c cắt nhau tại điểm C nên đáp án C sai.
Đáp án D sai vì ta thấy có ba cặp đường thẳng cắt nhau trên hình vẽ là a và c, a và b, b và c.
Cho hai tia Ox và Oy đối nhau. Lấy điểm G trên tia Ox, điểm H trên tia Oy. Ta có:
Điểm G nằm giữa hai điểm O và H
Điểm O nằm giữa hai điểm G và H
Điểm H nằm giữa hai điểm O và G
Không có điểm nào nằm giữa hai điểm còn lại
Đáp án : B
Dựa vào các dấu hiệu nhận biết một điểm nằm giữa hai điểm.
Nếu hai điểm A, B lần lượt thuộc hai tia đối nhau gốc O thì điểm O nằm giữa hai điểm A và B

Ta có Ox và Oy là hai tia đối nhau \(\left( {O \in xy} \right)\) và G thuộc tia Ox, H thuộc tia Oy nên điểm O nằm giữa hai điểm G và H.
Vẽ ba đường thẳng phân biệt bất kì, số giao điểm của ba đường thẳng đó không thể là:
$0$
$1$ hoặc $2$
$4$
$3$
Đáp án : C
Hai đường thẳng phân biệt bất kì có thể song song, cắt nhau, trùng nhau.
Với 3 đường thẳng phân biệt ta có các trường hợp sau:
+ Không có đường thẳng nào cắt nhau nên không có điểm chung.
+ Hai đường thẳng cắt nhau, đường thẳng còn lại không cắt hai đường thẳng đó, khi đó có 1 điểm chung.
+ Ba đường thẳng đó có đôi một cắt nhau thì có ba điểm chung.
Vậy không thể có trường hợp ba đường thẳng phân biệt bất kì mà có 4 điểm chung.
Cho hình vẽ. Em hãy chọn khẳng định sai:

NM và NI là hai tia đối nhau
IN và IM là hai tia trùng nhau
MN và MI là hai tia trùng nhau
MN và NI là hai tia trùng nhau
Đáp án : D
Dựa vào định nghĩa và tính chất các tia đối nhau và trùng nhau:
+ Hai tia đối nhau phải chung gốc, phải tạo thành 1 đường thẳng.
+ Hai tia trùng nhau là hai tia có chung gốc và có thêm ít nhất 1 điểm chung.
Từ hình vẽ ta thấy các điểm M, N, I cùng thuộc một đường thẳng.
+) Hai tia NM và NI đối nhau vì chúng chung gốc N và tạo thành một đường thẳng, từ đó loại đáp án A.
+) Hai tia IN và IM trùng nhau vì chúng chung gốc I và có thêm điểm chung là N, từ đó loại đáp án B.
+) Hai tia MN và MI trùng nhau vì chúng chung gốc M và có thêm điểm chung là N, từ đó loại đáp án C.
+) Hai tia MN và NI không trùng nhau vì chúng không chung gốc.
Cho L là điểm nằm giữa hai điểm I và K. Biết $IL = 2cm,{\rm{ }}LK = 5cm.$ Độ dài của đoạn thẳng IK là:
$3cm$
$2cm$
$5cm$
$7cm$
Đáp án : D
Vì L nằm giữa I và K nên ta áp dụng công thức cộng đoạn thẳng.

Vì L nằm giữa I và K nên ta có:\(IL + LK = IK \Rightarrow IK = 2 + 5 = 7cm\)
Cho đoạn thẳng $BC = 32cm.$ Gọi G là trung điểm của đoạn thẳng $BC,{\rm{ }}H$ là trung điểm của đoạn thẳng $GC.$ Khi đó, độ dài của đoạn thẳng BH là
$8cm$
$16cm$
$24cm$
$28cm$
Đáp án : C
Dựa vào tính chất trung điểm của đoạn thẳng: Nếu M là trung điểm của đoạn thẳng AB thì
${\rm{MA = MB}} = \dfrac{1}{2}AB$.

Vì G là trung điểm của đoạn thẳng BC nên ${\rm{BG = }}\,GC = \dfrac{1}{2}BC = \dfrac{1}{2} \cdot 32 = 16\,cm$.
Vì H là trung điểm của đoạn thẳng GC nên ${\rm{GH }} = HC = {\rm{ }}\dfrac{1}{2}GC = \dfrac{1}{2} \cdot 16 = 8\,cm$.
Ta có G thuộc đoạn thẳng BC nên GB và GC là hai tia đối nhau. (1)
Vì H là trung điểm của GC nên H thuộc GC (2)
Từ (1) và (2) suy ra G là điểm nằm giữa hai điểm B và H.
\(\begin{array}{l} \Rightarrow BG + GH = BH\\ \Rightarrow 16 + 8 = BH\\ \Rightarrow BH = 24cm\end{array}\)
Biết $IL = 4cm;{\rm{ }}LK = 5cm$ điều kiện để điểm I nằm giữa hai điểm L và K là:
\(IK=1cm\)
\(IK=9cm\)
\(IK=2cm\)
\(IK=3cm\)
Đáp án : A
Để điểm I nằm giữa hai điểm L và K là: $IL + IK = LK$
Điều kiện để điểm I nằm giữa hai điểm L và K là: \(IL + IK = LK\) nên \(4 + IK = 5 \Rightarrow IK = 5 - 4 = 1cm\)
Vậy điều kiện để điểm I nằm giữa hai điểm L và K là $IK = 1cm\;$
Biết $IL = 4cm;{\rm{ }}LK = 5cm$ điều kiện để điểm I nằm giữa hai điểm L và K là:
\(IK=1cm\)
\(IK=9cm\)
\(IK=2cm\)
\(IK=3cm\)
Đáp án : A
Để điểm I nằm giữa hai điểm L và K là: $IL + IK = LK$
Điều kiện để điểm I nằm giữa hai điểm L và K là: \(IL + IK = LK\) nên \(4 + IK = 5 \Rightarrow IK = 5 - 4 = 1cm\)
Vậy điều kiện để điểm I nằm giữa hai điểm L và K là $IK = 1cm\;$
Cho điểm I thuộc đoạn thẳng AB. Biết $AI = 5cm,AB = 8cm.$ Tính độ dài $BI.$
\(4cm\)
\(5cm\)
\(2cm\)
\(3cm\)
Đáp án : D
Bước 1: Chỉ ra điểm I nằm giữa hai điểm A và B Bước 2: Dựa vào tính chất cộng độ dài đoạn thẳng để tính IB
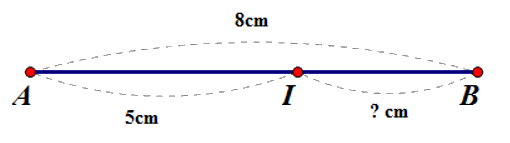
Vì điểm Ihuộc đoạn thẳng AB; $AI = 5cm,{\rm{ }}AB = 8cm$ mà $5cm < 8cm$ nên $AI < AB\;$
Suy ra điểm I nằm giữa hai điểm A và B $ \Rightarrow AI + IB = AB \Rightarrow 4cm + IB = 7cm \Rightarrow IB = 7cm - 4cm = 3cm$
Lấy năm điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng. Cứ qua hai điểm ta vẽ một đường thẳng. Số đường thẳng có thể vẽ được là:
$3$
$10$
$12$
$4$
Đáp án : B
Áp dụng tính chất: Chỉ có duy nhất một đường thẳng đi qua hai điểm phân biệt.
Từ 5 điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng ta có thể vẽ được các đường thẳng đi qua hai điểm bất kì như sau:
+ Với điểm M ta có thể nối với các điểm: N, P, Q, K để tạo thành 4 đường thẳng phân biệt.
+ Với điểm N ta có thể nối với các điểm: P, Q, K để tạo thành 3 đường thẳng phân biệt.
+ Với điểm P ta có thể nối với các điểm: Q, K để tạo thành 2 đường thẳng phân biệt.
+ Với điểm Q ta có thể nối với điểm K để tạo thành 1 đường thẳng .
Vậy từ 5 điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng ta có thể vẽ được tất cả:
4 + 3 + 2 + 1 = 10 đường thẳng phân biệt.
Cho trước 6 điểm trong đó có 4 điểm thẳng hàng. Vẽ các đoạn thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đoạn thẳng?
$15$
$16$
$14$
$13$
Đáp án : A
Vì qua hai điểm phân biệt ta luôn vẽ được một đoạn thẳng nên ta tính số đoạn thẳng tạo thành từ n điểm phân biệt theo công thức: \(\dfrac{{n\left( {n - 1} \right)}}{2}\,\,\left( {n \ge 2} \right)\) đoạn thẳng
Vì qua 2 điểm luôn vẽ được một đoạn thẳng Nên qua 6 điểm vẽ được số đoạn thẳng là: \(\dfrac{{6\left( {6 - 1} \right)}}{2} = 15\) (đoạn thẳng)
Cho 24 điểm trong đó có 6 điểm thẳng hàng. Qua 2 điểm ta kẻ được một đường thẳng. Hỏi kẻ được tất cả bao nhiêu đường thẳng?
\(276\)
\(290\)
\(262\)
\(226\)
Đáp án : C
Ta sử dụng công thức tính số đường thẳng tạo bởi n điểm phân biệt \(\left( {n \ge 2} \right)\) trong đó không có ba điểm nào thảng hàng: \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
+ Giả sử 24 điểm không có 3 điểm nào thẳng hàng. Tính số đường thẳng vẽ được qua 24 điểm + Tính số đường thẳng vẽ được qua 6 điểm (giả sử 6 điểm không có 3 điểm nào thẳng hàng)
+ Số đường thẳng vẽ được qua 6 điểm thẳng hàng+ Tính số đường thẳng vẽ được qua 24 điểm trong đó có 6 điểm thẳng hàng
Giả sử trong 24 điểm không có 3 điểm nào thẳng hàng tất cả vẽ được: $\dfrac{{24.(24 - 1)}}{2} = 276$ (đường thẳng) Qua 6 điểm thẳng hàng vẽ được số đường thẳng là: $\dfrac{{6.(6 - 1)}}{2} = 15$ (đường thẳng) Nhưng qua 6 điểm thẳng hàng chỉ vẽ được một đường thẳng Nên qua 24 điểm trong đó có 6 điểm thẳng hàng vẽ được: $276 - 15 + 1 = 262$ (đường thẳng)
Cho M thuộc đoạn thẳng AB, $AM = 4cm,{\rm{ }}AB = 6cm.$ Gọi O là trung điểm của đoạn AB.
Tính $MO$.
\(MO = 4cm\)
\(MO = 3cm\)
\(MO = 1cm\)
\(MO = 2cm\)
Đáp án: C
Áp dụng tính chất trung điểm của một đoạn thẳng và công thức cộng đoạn thẳng.

+) Vì \(M \in AB\) nên M nằm giữa A và B
\( \Rightarrow AM + MB = AB \Rightarrow BM \)\(= AB - MB = 6 - 4 = 2cm.\)
+) Vì O là trung điểm của AB nên: \(AO = OB = \dfrac{{AB}}{2} \)\(= \dfrac{6}{2} = 3cm\)
Vì \(O \in AB\), \(M \in AB\) và \(AO < AM (3cm < 4cm)\) nên O nằm giữa A và M suy ra:
\(AO + OM = AM \Rightarrow OM\)\( = AM - AO = 4 - 3 = 1cm\)
Trên AB lấy điểm I sao cho AI = 3,5cm. Lấy điểm P là trung điểm của AO. Chọn câu đúng.
Điểm I là trung điểm của OM
Điểm O nằm giữa I và P
\(IP = 2cm\)
Cả A, B, C đều đúng.
Đáp án: D
Áp dụng tính chất trung điểm của một đoạn thẳng và công thức cộng đoạn thẳng.

+ ) Vì \(O \in AB\), \(I \in AB\) và AO < AI (3cm < 3,5cm) nên O nằm giữa A và I suy ra:
\(AO + OI = AI \)\(\Rightarrow OI = AI - AO = 3,5 - 3 = 0,5cm\) (1)
Vì \(I \in AB\), \(M \in AB\) và AI < AM (3,5cm < 4cm) nên I nằm giữa A và M suy ra:
\(AI + IM = AM \Rightarrow IM = AM - AI = 4 - 3,5 = 0,5cm\)(2)
Từ (1) và (2) suy ra $OI = IM$ . (3)
Vì O nằm giữa A và I nên A và O nằm cùng phía đối với I . Mà I nằm giữa A và M nên A và M nằm khác phía đối với I \( \Rightarrow \) O và M nằm khác phía đối với I suy ra I nằm giữa M và O (4)
Từ (3) và (4) suy ra I là trung điểm của OM.
+) Vì P là trung điểm của AO nên: \(OP = AP = \dfrac{{AO}}{2} = \dfrac{3}{2} = 1,5cm\)
Vì $\left\{ \begin{array}{l}O,M \in AB\\AO < AM\left( {3cm < 4cm} \right)\end{array} \right. \Rightarrow $ O nằm giữa A và M
Suy ra A và M nằm khác phía đối với O
Vì P là trung điểm của AO nên A, P cùng phía đối với O.
Vì I là trung điểm của OM nên I, M cùng phía đối với O.
Từ đó suy ra I nằm giữa O và P \( \Rightarrow OP + IO = IP \)\(\Rightarrow IP = 1,5 + 0,5 = 2cm\)
Có bao nhiêu đường thẳng đi qua hai điểm phân biệt A và B?
\(1\)
\(2\)
\(3\)
Vô số
Cho hình vẽ. Em hãy chọn đáp án đúng.

A nằm giữa hai điểm B và C
B nằm giữa hai điểm A và C
C nằm giữa hai điểm A và B
Không có điểm nào nằm giữa hai điểm còn lại
Cho điểm M nằm giữa điểm N và P như hình vẽ. Kết luận nào sau đây là đúng ?

Tia NM trùng với tia MP
Tia MP trùng với tia NP
Tia PM trùng với tia PN
Tia MN trùng với tia MP.
Cho hình vẽ:

Hình vẽ trên có bao nhiêu tia chung gốc B:
$5$
$3$
$4$
$2$
Cho hình vẽ sau. Chọn câu đúng.

Điểm M thuộc đường thẳng xy nhưng không thuộc đường thẳng ab
Hai đường thẳng xy và ab không có điểm chung
Đường thẳng xy cắt đường thẳng ab tại M
Đường thẳng xy và ab có hai điểm chung
Cho hình vẽ sau. Chọn câu đúng.

\(P \in a;P \in c\)
\(Q \in b;Q \in c\)
Đường thẳng a cắt đường thẳng c tại điểm P
Không có hai đường thẳng nào cắt nhau trên hình vẽ
Cho hai tia Ox và Oy đối nhau. Lấy điểm G trên tia Ox, điểm H trên tia Oy. Ta có:
Điểm G nằm giữa hai điểm O và H
Điểm O nằm giữa hai điểm G và H
Điểm H nằm giữa hai điểm O và G
Không có điểm nào nằm giữa hai điểm còn lại
Vẽ ba đường thẳng phân biệt bất kì, số giao điểm của ba đường thẳng đó không thể là:
$0$
$1$ hoặc $2$
$4$
$3$
Cho hình vẽ. Em hãy chọn khẳng định sai:

NM và NI là hai tia đối nhau
IN và IM là hai tia trùng nhau
MN và MI là hai tia trùng nhau
MN và NI là hai tia trùng nhau
Cho L là điểm nằm giữa hai điểm I và K. Biết $IL = 2cm,{\rm{ }}LK = 5cm.$ Độ dài của đoạn thẳng IK là:
$3cm$
$2cm$
$5cm$
$7cm$
Cho đoạn thẳng $BC = 32cm.$ Gọi G là trung điểm của đoạn thẳng $BC,{\rm{ }}H$ là trung điểm của đoạn thẳng $GC.$ Khi đó, độ dài của đoạn thẳng BH là
$8cm$
$16cm$
$24cm$
$28cm$
Biết $IL = 4cm;{\rm{ }}LK = 5cm$ điều kiện để điểm I nằm giữa hai điểm L và K là:
\(IK=1cm\)
\(IK=9cm\)
\(IK=2cm\)
\(IK=3cm\)
Biết $IL = 4cm;{\rm{ }}LK = 5cm$ điều kiện để điểm I nằm giữa hai điểm L và K là:
\(IK=1cm\)
\(IK=9cm\)
\(IK=2cm\)
\(IK=3cm\)
Cho điểm I thuộc đoạn thẳng AB. Biết $AI = 5cm,AB = 8cm.$ Tính độ dài $BI.$
\(4cm\)
\(5cm\)
\(2cm\)
\(3cm\)
Lấy năm điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng. Cứ qua hai điểm ta vẽ một đường thẳng. Số đường thẳng có thể vẽ được là:
$3$
$10$
$12$
$4$
Cho trước 6 điểm trong đó có 4 điểm thẳng hàng. Vẽ các đoạn thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đoạn thẳng?
$15$
$16$
$14$
$13$
Cho 24 điểm trong đó có 6 điểm thẳng hàng. Qua 2 điểm ta kẻ được một đường thẳng. Hỏi kẻ được tất cả bao nhiêu đường thẳng?
\(276\)
\(290\)
\(262\)
\(226\)
Cho M thuộc đoạn thẳng AB, $AM = 4cm,{\rm{ }}AB = 6cm.$ Gọi O là trung điểm của đoạn AB.
Tính $MO$.
\(MO = 4cm\)
\(MO = 3cm\)
\(MO = 1cm\)
\(MO = 2cm\)
Trên AB lấy điểm I sao cho AI = 3,5cm. Lấy điểm P là trung điểm của AO. Chọn câu đúng.
Điểm I là trung điểm của OM
Điểm O nằm giữa I và P
\(IP = 2cm\)
Cả A, B, C đều đúng.
Có bao nhiêu đường thẳng đi qua hai điểm phân biệt A và B?
\(1\)
\(2\)
\(3\)
Vô số
Đáp án : A
Có 1 và chỉ 1 đường thẳng đi qua 2 điểm phân biệt cho trước.
Có 1 và chỉ 1 đường thẳng đi qua 2 điểm phân biệt cho trước. Vậy có duy nhất 1 đường thẳng đi qua hai điểm A và B.
Cho hình vẽ. Em hãy chọn đáp án đúng.

A nằm giữa hai điểm B và C
B nằm giữa hai điểm A và C
C nằm giữa hai điểm A và B
Không có điểm nào nằm giữa hai điểm còn lại
Đáp án : B
Quan sát hình vẽ và xác định điểm nằm giữa hai điểm còn lại
Quan sát hình vẽ ta thấy điểm B nằm giữa hai điểm A và C.
Cho điểm M nằm giữa điểm N và P như hình vẽ. Kết luận nào sau đây là đúng ?

Tia NM trùng với tia MP
Tia MP trùng với tia NP
Tia PM trùng với tia PN
Tia MN trùng với tia MP.
Đáp án : C
Hai tia trùng nhau là hai tia chung gốc và tạo thành nửa đường thẳng.
Nhận xét:
+ Đáp án A: Hai tia NM và MP là hai tia không chung gốc nên loại đáp án A.
+ Đáp án B: Hai tia MP và NP là hai tia không chung gốc nên loại đáp án B.
+ Đáp án C: thấy hai tia PN và PM là hai tia cùng chung gốc P và tạo thành nửa đường thẳng nên hai tia PN và PM là hai tia trùng nhau, do đó chọn đáp án C.
+ Đáp án D: Hai tia MN và MP là hai tia chung gốc nhưng tạo thành một đường thẳng nên hai tia MN và MP là hai tia đối nhau, do đó loại đáp án D.
Cho hình vẽ:

Hình vẽ trên có bao nhiêu tia chung gốc B:
$5$
$3$
$4$
$2$
Đáp án : A
Ta liệt kê tất cả các tia chung gốc B, kể cả các tia trùng nhau.

Hình vẽ trên có các tia chung gốc B là: BA, Bx, By, BC và BD. Vậy có tất cả 5 tia chung gốc B.
Cho hình vẽ sau. Chọn câu đúng.

Điểm M thuộc đường thẳng xy nhưng không thuộc đường thẳng ab
Hai đường thẳng xy và ab không có điểm chung
Đường thẳng xy cắt đường thẳng ab tại M
Đường thẳng xy và ab có hai điểm chung
Đáp án : C
Quan sát hình vẽ và sử dụng kiến thức về điểm, đường thẳng
Ta thấy hai đường thẳng xy và ab cắt nhau tại M nên đáp án C đúng.
Cho hình vẽ sau. Chọn câu đúng.

\(P \in a;P \in c\)
\(Q \in b;Q \in c\)
Đường thẳng a cắt đường thẳng c tại điểm P
Không có hai đường thẳng nào cắt nhau trên hình vẽ
Đáp án : B
Quan sát hình vẽ và sử dụng kiến thức về điểm và đường thẳng
Từ hình vẽ ta thấy \(P \in a;P \in c\) nên đáp án A sai; \(Q \in b;Q \in c\) nên đáp án B đúng.
Hai đường thẳng a và c cắt nhau tại điểm C nên đáp án C sai.
Đáp án D sai vì ta thấy có ba cặp đường thẳng cắt nhau trên hình vẽ là a và c, a và b, b và c.
Cho hai tia Ox và Oy đối nhau. Lấy điểm G trên tia Ox, điểm H trên tia Oy. Ta có:
Điểm G nằm giữa hai điểm O và H
Điểm O nằm giữa hai điểm G và H
Điểm H nằm giữa hai điểm O và G
Không có điểm nào nằm giữa hai điểm còn lại
Đáp án : B
Dựa vào các dấu hiệu nhận biết một điểm nằm giữa hai điểm.
Nếu hai điểm A, B lần lượt thuộc hai tia đối nhau gốc O thì điểm O nằm giữa hai điểm A và B

Ta có Ox và Oy là hai tia đối nhau \(\left( {O \in xy} \right)\) và G thuộc tia Ox, H thuộc tia Oy nên điểm O nằm giữa hai điểm G và H.
Vẽ ba đường thẳng phân biệt bất kì, số giao điểm của ba đường thẳng đó không thể là:
$0$
$1$ hoặc $2$
$4$
$3$
Đáp án : C
Hai đường thẳng phân biệt bất kì có thể song song, cắt nhau, trùng nhau.
Với 3 đường thẳng phân biệt ta có các trường hợp sau:
+ Không có đường thẳng nào cắt nhau nên không có điểm chung.
+ Hai đường thẳng cắt nhau, đường thẳng còn lại không cắt hai đường thẳng đó, khi đó có 1 điểm chung.
+ Ba đường thẳng đó có đôi một cắt nhau thì có ba điểm chung.
Vậy không thể có trường hợp ba đường thẳng phân biệt bất kì mà có 4 điểm chung.
Cho hình vẽ. Em hãy chọn khẳng định sai:

NM và NI là hai tia đối nhau
IN và IM là hai tia trùng nhau
MN và MI là hai tia trùng nhau
MN và NI là hai tia trùng nhau
Đáp án : D
Dựa vào định nghĩa và tính chất các tia đối nhau và trùng nhau:
+ Hai tia đối nhau phải chung gốc, phải tạo thành 1 đường thẳng.
+ Hai tia trùng nhau là hai tia có chung gốc và có thêm ít nhất 1 điểm chung.
Từ hình vẽ ta thấy các điểm M, N, I cùng thuộc một đường thẳng.
+) Hai tia NM và NI đối nhau vì chúng chung gốc N và tạo thành một đường thẳng, từ đó loại đáp án A.
+) Hai tia IN và IM trùng nhau vì chúng chung gốc I và có thêm điểm chung là N, từ đó loại đáp án B.
+) Hai tia MN và MI trùng nhau vì chúng chung gốc M và có thêm điểm chung là N, từ đó loại đáp án C.
+) Hai tia MN và NI không trùng nhau vì chúng không chung gốc.
Cho L là điểm nằm giữa hai điểm I và K. Biết $IL = 2cm,{\rm{ }}LK = 5cm.$ Độ dài của đoạn thẳng IK là:
$3cm$
$2cm$
$5cm$
$7cm$
Đáp án : D
Vì L nằm giữa I và K nên ta áp dụng công thức cộng đoạn thẳng.

Vì L nằm giữa I và K nên ta có:\(IL + LK = IK \Rightarrow IK = 2 + 5 = 7cm\)
Cho đoạn thẳng $BC = 32cm.$ Gọi G là trung điểm của đoạn thẳng $BC,{\rm{ }}H$ là trung điểm của đoạn thẳng $GC.$ Khi đó, độ dài của đoạn thẳng BH là
$8cm$
$16cm$
$24cm$
$28cm$
Đáp án : C
Dựa vào tính chất trung điểm của đoạn thẳng: Nếu M là trung điểm của đoạn thẳng AB thì
${\rm{MA = MB}} = \dfrac{1}{2}AB$.

Vì G là trung điểm của đoạn thẳng BC nên ${\rm{BG = }}\,GC = \dfrac{1}{2}BC = \dfrac{1}{2} \cdot 32 = 16\,cm$.
Vì H là trung điểm của đoạn thẳng GC nên ${\rm{GH }} = HC = {\rm{ }}\dfrac{1}{2}GC = \dfrac{1}{2} \cdot 16 = 8\,cm$.
Ta có G thuộc đoạn thẳng BC nên GB và GC là hai tia đối nhau. (1)
Vì H là trung điểm của GC nên H thuộc GC (2)
Từ (1) và (2) suy ra G là điểm nằm giữa hai điểm B và H.
\(\begin{array}{l} \Rightarrow BG + GH = BH\\ \Rightarrow 16 + 8 = BH\\ \Rightarrow BH = 24cm\end{array}\)
Biết $IL = 4cm;{\rm{ }}LK = 5cm$ điều kiện để điểm I nằm giữa hai điểm L và K là:
\(IK=1cm\)
\(IK=9cm\)
\(IK=2cm\)
\(IK=3cm\)
Đáp án : A
Để điểm I nằm giữa hai điểm L và K là: $IL + IK = LK$
Điều kiện để điểm I nằm giữa hai điểm L và K là: \(IL + IK = LK\) nên \(4 + IK = 5 \Rightarrow IK = 5 - 4 = 1cm\)
Vậy điều kiện để điểm I nằm giữa hai điểm L và K là $IK = 1cm\;$
Biết $IL = 4cm;{\rm{ }}LK = 5cm$ điều kiện để điểm I nằm giữa hai điểm L và K là:
\(IK=1cm\)
\(IK=9cm\)
\(IK=2cm\)
\(IK=3cm\)
Đáp án : A
Để điểm I nằm giữa hai điểm L và K là: $IL + IK = LK$
Điều kiện để điểm I nằm giữa hai điểm L và K là: \(IL + IK = LK\) nên \(4 + IK = 5 \Rightarrow IK = 5 - 4 = 1cm\)
Vậy điều kiện để điểm I nằm giữa hai điểm L và K là $IK = 1cm\;$
Cho điểm I thuộc đoạn thẳng AB. Biết $AI = 5cm,AB = 8cm.$ Tính độ dài $BI.$
\(4cm\)
\(5cm\)
\(2cm\)
\(3cm\)
Đáp án : D
Bước 1: Chỉ ra điểm I nằm giữa hai điểm A và B Bước 2: Dựa vào tính chất cộng độ dài đoạn thẳng để tính IB

Vì điểm Ihuộc đoạn thẳng AB; $AI = 5cm,{\rm{ }}AB = 8cm$ mà $5cm < 8cm$ nên $AI < AB\;$
Suy ra điểm I nằm giữa hai điểm A và B $ \Rightarrow AI + IB = AB \Rightarrow 4cm + IB = 7cm \Rightarrow IB = 7cm - 4cm = 3cm$
Lấy năm điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng. Cứ qua hai điểm ta vẽ một đường thẳng. Số đường thẳng có thể vẽ được là:
$3$
$10$
$12$
$4$
Đáp án : B
Áp dụng tính chất: Chỉ có duy nhất một đường thẳng đi qua hai điểm phân biệt.
Từ 5 điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng ta có thể vẽ được các đường thẳng đi qua hai điểm bất kì như sau:
+ Với điểm M ta có thể nối với các điểm: N, P, Q, K để tạo thành 4 đường thẳng phân biệt.
+ Với điểm N ta có thể nối với các điểm: P, Q, K để tạo thành 3 đường thẳng phân biệt.
+ Với điểm P ta có thể nối với các điểm: Q, K để tạo thành 2 đường thẳng phân biệt.
+ Với điểm Q ta có thể nối với điểm K để tạo thành 1 đường thẳng .
Vậy từ 5 điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng ta có thể vẽ được tất cả:
4 + 3 + 2 + 1 = 10 đường thẳng phân biệt.
Cho trước 6 điểm trong đó có 4 điểm thẳng hàng. Vẽ các đoạn thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đoạn thẳng?
$15$
$16$
$14$
$13$
Đáp án : A
Vì qua hai điểm phân biệt ta luôn vẽ được một đoạn thẳng nên ta tính số đoạn thẳng tạo thành từ n điểm phân biệt theo công thức: \(\dfrac{{n\left( {n - 1} \right)}}{2}\,\,\left( {n \ge 2} \right)\) đoạn thẳng
Vì qua 2 điểm luôn vẽ được một đoạn thẳng Nên qua 6 điểm vẽ được số đoạn thẳng là: \(\dfrac{{6\left( {6 - 1} \right)}}{2} = 15\) (đoạn thẳng)
Cho 24 điểm trong đó có 6 điểm thẳng hàng. Qua 2 điểm ta kẻ được một đường thẳng. Hỏi kẻ được tất cả bao nhiêu đường thẳng?
\(276\)
\(290\)
\(262\)
\(226\)
Đáp án : C
Ta sử dụng công thức tính số đường thẳng tạo bởi n điểm phân biệt \(\left( {n \ge 2} \right)\) trong đó không có ba điểm nào thảng hàng: \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
+ Giả sử 24 điểm không có 3 điểm nào thẳng hàng. Tính số đường thẳng vẽ được qua 24 điểm + Tính số đường thẳng vẽ được qua 6 điểm (giả sử 6 điểm không có 3 điểm nào thẳng hàng)
+ Số đường thẳng vẽ được qua 6 điểm thẳng hàng+ Tính số đường thẳng vẽ được qua 24 điểm trong đó có 6 điểm thẳng hàng
Giả sử trong 24 điểm không có 3 điểm nào thẳng hàng tất cả vẽ được: $\dfrac{{24.(24 - 1)}}{2} = 276$ (đường thẳng) Qua 6 điểm thẳng hàng vẽ được số đường thẳng là: $\dfrac{{6.(6 - 1)}}{2} = 15$ (đường thẳng) Nhưng qua 6 điểm thẳng hàng chỉ vẽ được một đường thẳng Nên qua 24 điểm trong đó có 6 điểm thẳng hàng vẽ được: $276 - 15 + 1 = 262$ (đường thẳng)
Cho M thuộc đoạn thẳng AB, $AM = 4cm,{\rm{ }}AB = 6cm.$ Gọi O là trung điểm của đoạn AB.
Tính $MO$.
\(MO = 4cm\)
\(MO = 3cm\)
\(MO = 1cm\)
\(MO = 2cm\)
Đáp án: C
Áp dụng tính chất trung điểm của một đoạn thẳng và công thức cộng đoạn thẳng.

+) Vì \(M \in AB\) nên M nằm giữa A và B
\( \Rightarrow AM + MB = AB \Rightarrow BM \)\(= AB - MB = 6 - 4 = 2cm.\)
+) Vì O là trung điểm của AB nên: \(AO = OB = \dfrac{{AB}}{2} \)\(= \dfrac{6}{2} = 3cm\)
Vì \(O \in AB\), \(M \in AB\) và \(AO < AM (3cm < 4cm)\) nên O nằm giữa A và M suy ra:
\(AO + OM = AM \Rightarrow OM\)\( = AM - AO = 4 - 3 = 1cm\)
Trên AB lấy điểm I sao cho AI = 3,5cm. Lấy điểm P là trung điểm của AO. Chọn câu đúng.
Điểm I là trung điểm của OM
Điểm O nằm giữa I và P
\(IP = 2cm\)
Cả A, B, C đều đúng.
Đáp án: D
Áp dụng tính chất trung điểm của một đoạn thẳng và công thức cộng đoạn thẳng.

+ ) Vì \(O \in AB\), \(I \in AB\) và AO < AI (3cm < 3,5cm) nên O nằm giữa A và I suy ra:
\(AO + OI = AI \)\(\Rightarrow OI = AI - AO = 3,5 - 3 = 0,5cm\) (1)
Vì \(I \in AB\), \(M \in AB\) và AI < AM (3,5cm < 4cm) nên I nằm giữa A và M suy ra:
\(AI + IM = AM \Rightarrow IM = AM - AI = 4 - 3,5 = 0,5cm\)(2)
Từ (1) và (2) suy ra $OI = IM$ . (3)
Vì O nằm giữa A và I nên A và O nằm cùng phía đối với I . Mà I nằm giữa A và M nên A và M nằm khác phía đối với I \( \Rightarrow \) O và M nằm khác phía đối với I suy ra I nằm giữa M và O (4)
Từ (3) và (4) suy ra I là trung điểm của OM.
+) Vì P là trung điểm của AO nên: \(OP = AP = \dfrac{{AO}}{2} = \dfrac{3}{2} = 1,5cm\)
Vì $\left\{ \begin{array}{l}O,M \in AB\\AO < AM\left( {3cm < 4cm} \right)\end{array} \right. \Rightarrow $ O nằm giữa A và M
Suy ra A và M nằm khác phía đối với O
Vì P là trung điểm của AO nên A, P cùng phía đối với O.
Vì I là trung điểm của OM nên I, M cùng phía đối với O.
Từ đó suy ra I nằm giữa O và P \( \Rightarrow OP + IO = IP \)\(\Rightarrow IP = 1,5 + 0,5 = 2cm\)
Chương 8 Toán 6 Chân trời sáng tạo tập trung vào việc giới thiệu và làm quen với các khái niệm cơ bản của hình học phẳng. Đây là nền tảng quan trọng để học sinh tiếp thu các kiến thức phức tạp hơn ở các lớp trên. Việc nắm vững các khái niệm về điểm, đường thẳng, đoạn thẳng, tia, góc và các loại góc là vô cùng cần thiết.
1. Điểm và đường thẳng: Điểm là một khái niệm cơ bản trong hình học, được hiểu là vị trí xác định. Đường thẳng là tập hợp các điểm liên tiếp nhau, kéo dài vô hạn về hai phía. Hai điểm xác định một đường thẳng duy nhất.
2. Đoạn thẳng: Đoạn thẳng là một phần của đường thẳng, giới hạn bởi hai điểm. Độ dài của đoạn thẳng là khoảng cách giữa hai điểm đó.
3. Tia: Tia là một phần của đường thẳng, có một điểm đầu và kéo dài vô hạn về một phía.
4. Góc: Góc là hình tạo bởi hai tia chung gốc. Góc được đo bằng độ (°).
1. Góc nhọn: Góc có số đo nhỏ hơn 90°.
2. Góc vuông: Góc có số đo bằng 90°.
3. Góc tù: Góc có số đo lớn hơn 90° và nhỏ hơn 180°.
4. Góc bẹt: Góc có số đo bằng 180°.
1. Đường tròn: Đường tròn là tập hợp các điểm cách một điểm cố định (tâm) một khoảng không đổi (bán kính).
2. Tam giác: Tam giác là hình có ba cạnh và ba góc. Có nhiều loại tam giác khác nhau như tam giác đều, tam giác cân, tam giác vuông.
3. Tứ giác: Tứ giác là hình có bốn cạnh và bốn góc. Có nhiều loại tứ giác khác nhau như hình vuông, hình chữ nhật, hình thoi, hình bình hành.
Để nắm vững kiến thức về chương 8, các em cần thực hành giải nhiều bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập trắc nghiệm đa dạng, giúp các em rèn luyện kỹ năng và tự tin hơn trong các kỳ thi.
Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!