Bài tập trắc nghiệm này được thiết kế để giúp học sinh lớp 6 ôn luyện và kiểm tra kiến thức về khái niệm ba điểm thẳng hàng, ba điểm không thẳng hàng. Bài tập bao gồm nhiều dạng câu hỏi khác nhau, từ nhận biết đến vận dụng, giúp học sinh hiểu sâu sắc hơn về chủ đề này.
Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm chất lượng cao, có đáp án chi tiết và giải thích rõ ràng, giúp học sinh tự học hiệu quả và đạt kết quả tốt trong các bài kiểm tra.
Chọn câu đúng.
Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó không thẳng hàng
Nếu ba điểm không cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng
Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng
Cả ba đáp án trên đều sai.
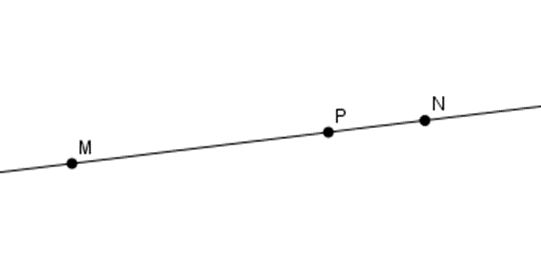
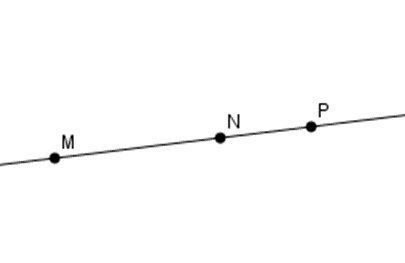
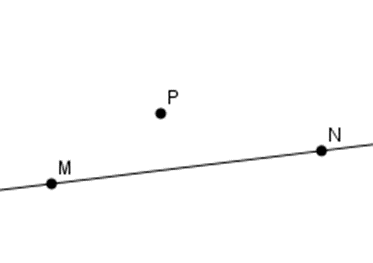
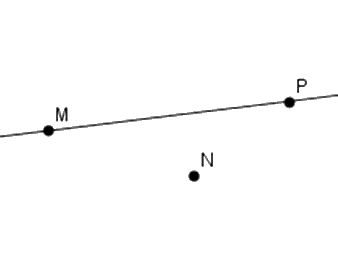
Cho ba điểm \(M;N;P\) thẳng hàng với \(P\) nằm giữa \(M\) và \(N.\) Chọn hình vẽ đúng.
Kể tên bộ ba điểm thẳng hàng trong hình vẽ dưới đây.
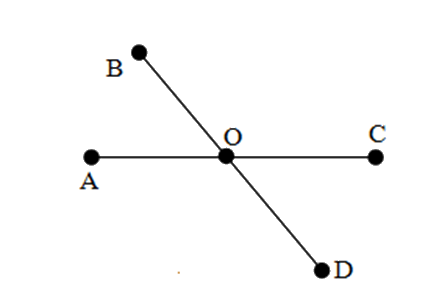
\(A,O,D\) và \(B,O,C\)
\(A,O,B\) và \(C,O,D\)
\(A,O,C\) và \(B,O,D\)
\(A,O,C\) và \(B,O,A\)
Có bao nhiêu bộ ba điểm thẳng hàng trên hình vẽ sau:
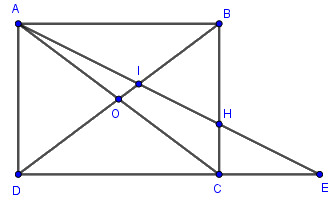
\(10\)
\(11\)
\(12\)
\(13\)
Cho hình vẽ sau. Chọn câu sai.
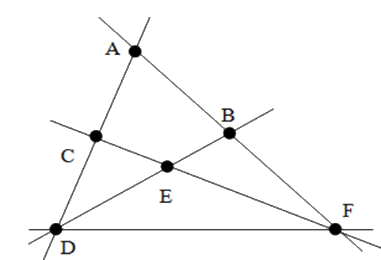
Ba điểm \(D;E;B\) thẳng hàng
Ba điểm \(C;E;A\) không thẳng hàng
Ba điểm \(A;B;F\) thẳng hàng
Ba điểm \(D;E;F\) thẳng hàng
Có bao nhiêu bộ ba điểm thẳng hàng trong hình vẽ dưới đây?
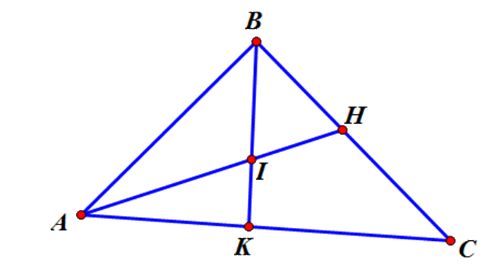
\(7\)
\(4\)
\(5\)
\(6\)
Có bao nhiêu bộ ba điểm không thẳng hàng trong hình vẽ sau
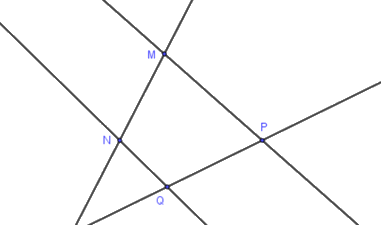
\(3\)
\(5\)
\(4\)
\(6\)
Cho bốn điểm $M;N;P;Q$ cùng nằm trên một đường thẳng và hai điểm $M;N$ nằm cùng phía đối với điểm $Q$ còn hai điểm $N,P$ nằm khác phía đối với điểm $Q.$ Một hình vẽ đúng là:
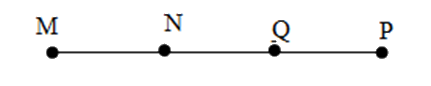
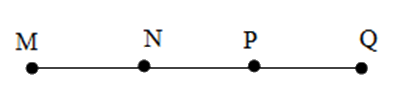
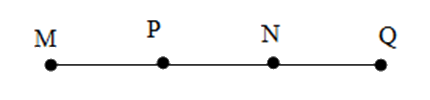
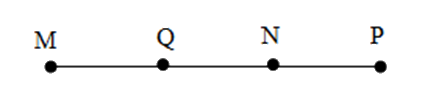
Cho $5$ điểm $A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D,{\rm{ }}O$ sao cho $3$ điểm $A,{\rm{ }}B,{\rm{ }}C$ cùng thuộc đường thẳng $d;$ $3$ điểm $B,{\rm{ }}C,{\rm{ }}D$ thẳng hàng và $3$ điểm $C,{\rm{ }}D,{\rm{ }}O$ không thẳng hàng. Hỏi điểm nào nằm ngoài đường thẳng $d?$
\(O,A\)
\(O\)
\(D\)
\(C,D\)
Cho hình vẽ sau:
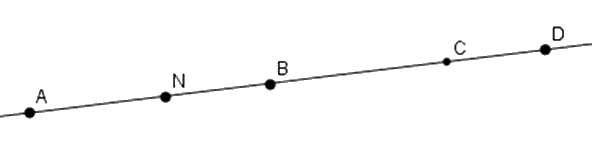
Kể tên các điểm nằm giữa \(A\) và \(D.\)
\(N,B,C\)
\(B,C,D\)
\(N\)
\(B,C\)
Có bao nhiêu điểm nằm giữa \(N\) và \(D?\)
\(3\)
\(1\)
\(2\)
\(0\)
Số cặp điểm nằm cùng phía với điểm \(A\) là:
\(9\)
\(18\)
\(12\)
\(6\)
Trên hình vẽ, điểm \(B\) nằm giữa bao nhiêu cặp điểm?
\(10\)
\(8\)
\(4\)
\(6\)
Cho hình vẽ sau:

Trên hình vẽ, điểm \(B\) và \(D\) nằm khác phía với mấy điểm?
\(0\)
\(3\)
\(4\)
\(1\)
Trên hình vẽ, điểm \(A\) và \(B\) nằm cùng phía với các điểm nào?
điểm \(C\)
điểm \(D\)
điểm \(B\)
Cả điểm \(C\) và điểm \(D\)
Điểm \(A\) và \(C\) nằm cùng phía với điểm nào?
điểm \(D\)
điểm \(B\)
điểm \(A\)
Cả điểm \(D\) và điểm \(B\)
Chọn câu sai.
Điểm \(B\) nằm giữa \(A\) và \(C.\)
Điểm \(B\) nằm giữa \(A\) và \(D.\)
Điểm \(C\) nằm giữa \(A\) và \(B.\)
Điểm \(C\) nằm giữa \(D\) và \(A.\)
Lời giải và đáp án
Chọn câu đúng.
Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó không thẳng hàng
Nếu ba điểm không cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng
Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng
Cả ba đáp án trên đều sai.
Đáp án : C
Định nghĩa ba điểm thẳng hàng, không thẳng hàng:
+ Khi ba điểm cùng thuộc một đường thẳng, ta nói là ba điểm thẳng hàng.
+ Khi ba điểm không cùng thuộc bất kì đường thẳng nào, ta nói chúng không thẳng hàng.
Từ định nghĩa ba điểm thẳng hàng ta thấy đáp án C đúng.
Cho ba điểm \(M;N;P\) thẳng hàng với \(P\) nằm giữa \(M\) và \(N.\) Chọn hình vẽ đúng.
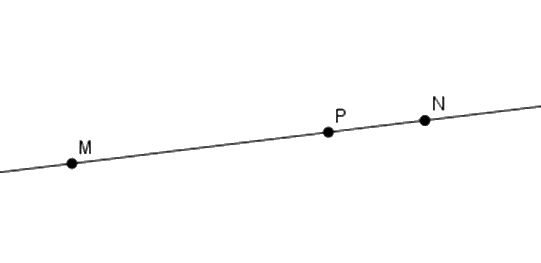
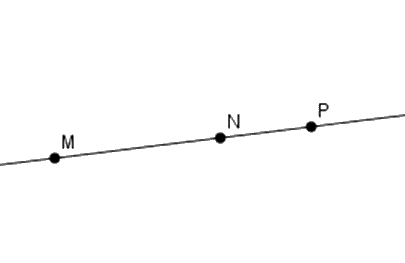
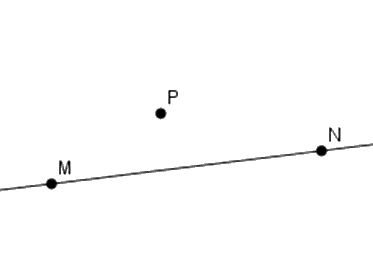
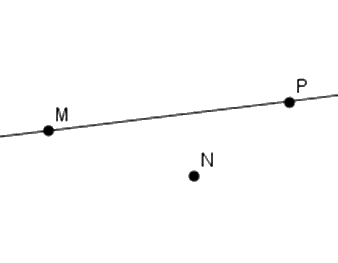
Đáp án : A
Xét từng đáp án:
- Kiểm tra xem ba điểm \(M,N,P\) có thẳng hàng hay không.
- Kiểm tra điểm \(P\) nằm giữa hai điểm \(M,N\)
Đáp án A: Ta thấy ba điểm \(M,N,P\) thẳng hàng và điểm \(P\) nằm giữa hai điểm \(M,N\) nên A đúng.
Đáp án B: Ta thấy ba điểm \(M,N,P\) thẳng hàng và điểm \(P\) không nằm giữa hai điểm \(M,N\) nên B sai.
Đáp án C: Ta thấy ba điểm \(M,N,P\) không thẳng hàng nên C sai.
Đáp án D: Ta thấy ba điểm \(M,N,P\) không thẳng hàng nên D sai.
Kể tên bộ ba điểm thẳng hàng trong hình vẽ dưới đây.
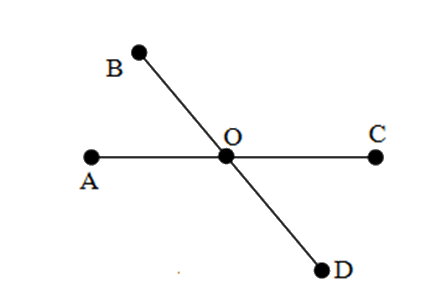
\(A,O,D\) và \(B,O,C\)
\(A,O,B\) và \(C,O,D\)
\(A,O,C\) và \(B,O,D\)
\(A,O,C\) và \(B,O,A\)
Đáp án : C
Ba điểm cùng thuộc một đường thẳng thì chúng thẳng hàng.
Các bộ ba điểm thẳng hàng trong hình vẽ là:
\(A,O,C\) và \(B,O,D\)
Có bao nhiêu bộ ba điểm thẳng hàng trên hình vẽ sau:
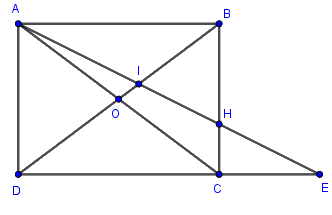
\(10\)
\(11\)
\(12\)
\(13\)
Đáp án : B
Tìm các bộ ba điểm thẳng hàng và kết luận.
Chú ý:
Ba điểm cùng thuộc một đường thẳng thì chúng thẳng hàng.
Các bộ ba điểm thẳng hàng trong hình vẽ là:
\(\left( {A,O,C} \right),\left( {B,O,D} \right),\left( {D,C,E} \right),\) \(\left( {B,H,C} \right),\left( {A,I,H} \right),\left( {A,I,E} \right),\) \(\left( {A,H,E} \right),\left( {I,H,E} \right),\left( {D,O,I} \right),\) \(\left( {D,I,B} \right),\left( {O,I,B} \right)\)
Vậy có tất cả \(11\) bộ ba điểm thẳng hàng trong hình vẽ.
Cho hình vẽ sau. Chọn câu sai.
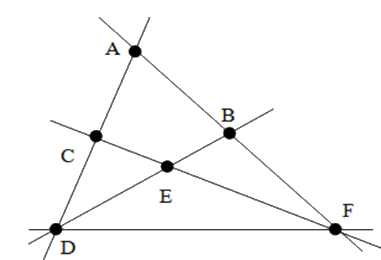
Ba điểm \(D;E;B\) thẳng hàng
Ba điểm \(C;E;A\) không thẳng hàng
Ba điểm \(A;B;F\) thẳng hàng
Ba điểm \(D;E;F\) thẳng hàng
Đáp án : D
Quan sát hình vẽ, nhận xét tính đúng sai của từng đáp án, sử dungj định nghĩa ba điểm thẳng hàng: ba điểm cùng thuộc một đường thẳng thì chúng thẳng hàng.
Đáp án A: Ba điểm \(D,E,B\) thẳng hàng nên A đúng.
Đáp án B: Ba điểm \(C;E;A\) không thẳng hàng nên B đúng.
Đáp án C: Ba điểm \(A;B;F\) thẳng hàng nên C đúng.
Đáp án D: Ba điểm \(D;E;F\) không thẳng hàng nên D sai.
Có bao nhiêu bộ ba điểm thẳng hàng trong hình vẽ dưới đây?
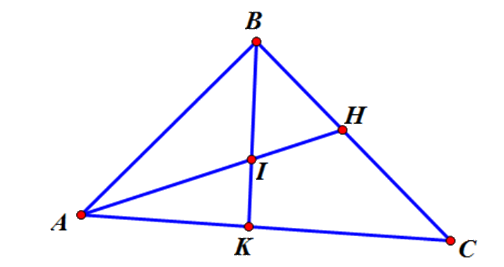
\(7\)
\(4\)
\(5\)
\(6\)
Đáp án : B
Liệt kê các bộ ba điểm thẳng hàng trong hình vẽ và kết luận.
Các bộ ba điểm thẳng hàng trong hình vẽ là:
\(\left( {A,I,H} \right),\left( {B,I,K} \right),\) \(\left( {A,K,C} \right),\left( {B,H,C} \right).\)
Vậy có \(4\) cặp điểm thỏa mãn bài toán.
Có bao nhiêu bộ ba điểm không thẳng hàng trong hình vẽ sau
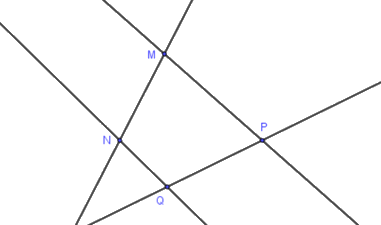
\(3\)
\(5\)
\(4\)
\(6\)
Đáp án : C
Liệt kê các bộ ba điểm không thẳng hàng và kết luận.
Các bộ ba điểm trong hình vẽ là:
\(\left( {M,N,P} \right),\left( {M,N,Q} \right),\) \(\left( {M,P,Q} \right),\left( {N,P,Q} \right)\)
Vậy có \(4\) bộ ba điểm không thẳng hàng.
Cho bốn điểm $M;N;P;Q$ cùng nằm trên một đường thẳng và hai điểm $M;N$ nằm cùng phía đối với điểm $Q$ còn hai điểm $N,P$ nằm khác phía đối với điểm $Q.$ Một hình vẽ đúng là:
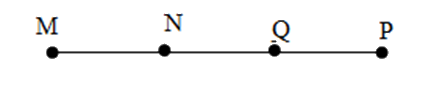
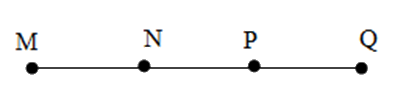
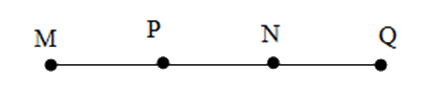
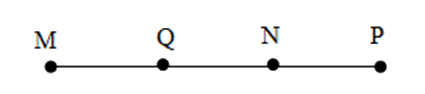
Đáp án : A
Quan sát hình vẽ ở các đáp án, đối chiếu với yêu cầu bài cho rồi kết luận
Đáp án A: Hai điểm \(M,N\) nằm cùng phía so với \(Q\) và hai điểm \(N,P\) khác phía so với \(Q\) nên thỏa mãn, chọn A.
Đáp án B: Hai điểm \(N,P\) cùng phía so với \(Q\) nên không thỏa mãn, loại B.
Đáp án C: Hai điểm \(N,P\) cùng phía so với \(Q\) nên không thỏa mãn, loại C.
Đáp án D: Hai điểm \(M,N\) nằm khác phía so với \(Q\) nên không thỏa mãn, loại D.
Cho $5$ điểm $A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D,{\rm{ }}O$ sao cho $3$ điểm $A,{\rm{ }}B,{\rm{ }}C$ cùng thuộc đường thẳng $d;$ $3$ điểm $B,{\rm{ }}C,{\rm{ }}D$ thẳng hàng và $3$ điểm $C,{\rm{ }}D,{\rm{ }}O$ không thẳng hàng. Hỏi điểm nào nằm ngoài đường thẳng $d?$
\(O,A\)
\(O\)
\(D\)
\(C,D\)
Đáp án : B
Vẽ hình theo yêu cầu bài toán và kết luận dựa vào định nghĩa ba diểm thẳng hàng:
Ba điểm cùng thuộc một đường thẳng thì chúng thẳng hàng hoặc ba điểm thẳng hàng thì cùng thuộc một đường thẳng.
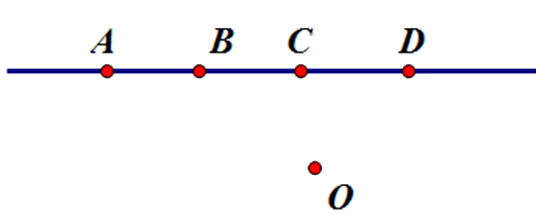
Vì ba điểm \(A,B,C\) thuộc \(d\) và \(B,C,D\) thẳng hàng nên \(D \in d\)
Mà \(C,D \in d\) nên nếu \(C,D,O\) không thẳng hàng thì \(O \notin d\)
Vậy điểm \(O\) không thuộc đường thẳng \(d\)
Cho hình vẽ sau:
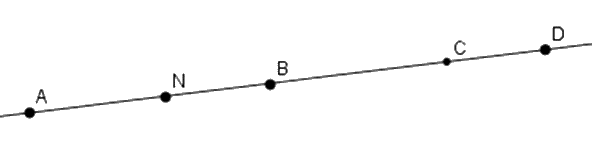
Kể tên các điểm nằm giữa \(A\) và \(D.\)
\(N,B,C\)
\(B,C,D\)
\(N\)
\(B,C\)
Đáp án: A
Quan sát hĩnh vẽ và tìm các điểm nằm giữa \(A\) và \(D\)
Các điểm nằm giữa \(A\) và \(D\) là \(N,B,C\)
Có bao nhiêu điểm nằm giữa \(N\) và \(D?\)
\(3\)
\(1\)
\(2\)
\(0\)
Đáp án: C
Tìm các điểm nằm giữa hai điểm \(N,D\) rồi kết luận.
Các điểm nằm giữa \(N\) và \(D\) là \(B,C\)
Vậy có \(2\) điểm cần tìm.
Số cặp điểm nằm cùng phía với điểm \(A\) là:
\(9\)
\(18\)
\(12\)
\(6\)
Đáp án: D
Liệt kê tất cả các cặp điểm nằm cùng phía với điểm \(A\)
Các cặp điểm nằm cùng phía so với điểm \(A\) là:
\(\left( {N,B} \right),\left( {N,C} \right),\left( {N,D} \right),\) \(\left( {B,C} \right),\left( {B,D} \right),\left( {C,D} \right)\)
Vậy có \(6\) cặp điểm thỏa mãn bài toán.
Trên hình vẽ, điểm \(B\) nằm giữa bao nhiêu cặp điểm?
\(10\)
\(8\)
\(4\)
\(6\)
Đáp án: C
Liệt kê các cặp điểm thỏa mãn điểm \(B\) nằm giữa.
Điểm \(B\) nằm giữa các cặp điểm là:
\(\left( {N,C} \right),\left( {A,D} \right),\left( {A,C} \right),\left( {N,D} \right)\)
Vậy có \(4\) cặp điểm thỏa mãn bài toán.
Cho hình vẽ sau:

Trên hình vẽ, điểm \(B\) và \(D\) nằm khác phía với mấy điểm?
\(0\)
\(3\)
\(4\)
\(1\)
Đáp án: D
Tìm số điểm nằm giữa hai điểm \(B,D\) trong hình vẽ rồi suy ra kết luận.
Sử dụng kiến thức: Nếu điểm \(B\) nằm giữa hai điểm \(A,C\) thì ta nói hai điểm \(A,C\) nằm khác phía so với \(B\).
Trong hình vẽ chỉ có điểm \(C\) nằm giữa hai điểm \(B\) và \(D\) nên chỉ có \(1\) điểm thỏa mãn yêu cầu bài toán.
Trên hình vẽ, điểm \(A\) và \(B\) nằm cùng phía với các điểm nào?
điểm \(C\)
điểm \(D\)
điểm \(B\)
Cả điểm \(C\) và điểm \(D\)
Đáp án: D
Sử dụng kiến thức: Nếu điểm \(B\) nằm giữa hai điểm \(A,C\) thì ta nói hai điểm \(A,B\) nằm cùng phía so với \(C\) và \(B,C\) nằm cùng phía so với \(A\).
Trên hình vẽ, hai điểm \(A,B\) nằm cùng phía so với các điểm \(C,D\).
Điểm \(A\) và \(C\) nằm cùng phía với điểm nào?
điểm \(D\)
điểm \(B\)
điểm \(A\)
Cả điểm \(D\) và điểm \(B\)
Đáp án: A
Sử dụng kiến thức: Nếu điểm \(B\) nằm giữa hai điểm \(A,C\) thì ta nói hai điểm \(A,B\) nằm cùng phía so với \(C\) và \(B,C\) nằm cùng phía so với \(A\).
Trên hình vẽ, hai điểm \(A,C\) nằm cùng phía so với điểm \(D\) và nằm khác phía so với điểm \(B\).
Chọn câu sai.
Điểm \(B\) nằm giữa \(A\) và \(C.\)
Điểm \(B\) nằm giữa \(A\) và \(D.\)
Điểm \(C\) nằm giữa \(A\) và \(B.\)
Điểm \(C\) nằm giữa \(D\) và \(A.\)
Đáp án: C
Quan sát hình vẽ và nhận xét tính đúng sai của từng đáp án.
Chú ý: Trong ba điểm thẳng hàng chỉ có \(1\) điểm nằm giữa hai điểm còn lại.
Đáp án A: Điểm \(B\) nằm giữa \(A\) và \(C\) nên A đúng và C sai.
Đáp án B: Điểm \(B\) nằm giữa \(A\) và \(D\) nên B đúng.
Điểm \(C\) nằm giữa \(D\) và \(A\) nên D đúng.
Chọn câu đúng.
Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó không thẳng hàng
Nếu ba điểm không cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng
Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng
Cả ba đáp án trên đều sai.
Cho ba điểm \(M;N;P\) thẳng hàng với \(P\) nằm giữa \(M\) và \(N.\) Chọn hình vẽ đúng.




Kể tên bộ ba điểm thẳng hàng trong hình vẽ dưới đây.

\(A,O,D\) và \(B,O,C\)
\(A,O,B\) và \(C,O,D\)
\(A,O,C\) và \(B,O,D\)
\(A,O,C\) và \(B,O,A\)
Có bao nhiêu bộ ba điểm thẳng hàng trên hình vẽ sau:

\(10\)
\(11\)
\(12\)
\(13\)
Cho hình vẽ sau. Chọn câu sai.

Ba điểm \(D;E;B\) thẳng hàng
Ba điểm \(C;E;A\) không thẳng hàng
Ba điểm \(A;B;F\) thẳng hàng
Ba điểm \(D;E;F\) thẳng hàng
Có bao nhiêu bộ ba điểm thẳng hàng trong hình vẽ dưới đây?

\(7\)
\(4\)
\(5\)
\(6\)
Có bao nhiêu bộ ba điểm không thẳng hàng trong hình vẽ sau

\(3\)
\(5\)
\(4\)
\(6\)
Cho bốn điểm $M;N;P;Q$ cùng nằm trên một đường thẳng và hai điểm $M;N$ nằm cùng phía đối với điểm $Q$ còn hai điểm $N,P$ nằm khác phía đối với điểm $Q.$ Một hình vẽ đúng là:
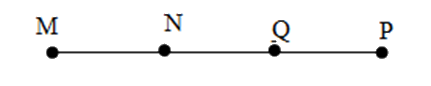


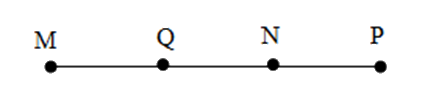
Cho $5$ điểm $A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D,{\rm{ }}O$ sao cho $3$ điểm $A,{\rm{ }}B,{\rm{ }}C$ cùng thuộc đường thẳng $d;$ $3$ điểm $B,{\rm{ }}C,{\rm{ }}D$ thẳng hàng và $3$ điểm $C,{\rm{ }}D,{\rm{ }}O$ không thẳng hàng. Hỏi điểm nào nằm ngoài đường thẳng $d?$
\(O,A\)
\(O\)
\(D\)
\(C,D\)
Cho hình vẽ sau:

Kể tên các điểm nằm giữa \(A\) và \(D.\)
\(N,B,C\)
\(B,C,D\)
\(N\)
\(B,C\)
Có bao nhiêu điểm nằm giữa \(N\) và \(D?\)
\(3\)
\(1\)
\(2\)
\(0\)
Số cặp điểm nằm cùng phía với điểm \(A\) là:
\(9\)
\(18\)
\(12\)
\(6\)
Trên hình vẽ, điểm \(B\) nằm giữa bao nhiêu cặp điểm?
\(10\)
\(8\)
\(4\)
\(6\)
Cho hình vẽ sau:

Trên hình vẽ, điểm \(B\) và \(D\) nằm khác phía với mấy điểm?
\(0\)
\(3\)
\(4\)
\(1\)
Trên hình vẽ, điểm \(A\) và \(B\) nằm cùng phía với các điểm nào?
điểm \(C\)
điểm \(D\)
điểm \(B\)
Cả điểm \(C\) và điểm \(D\)
Điểm \(A\) và \(C\) nằm cùng phía với điểm nào?
điểm \(D\)
điểm \(B\)
điểm \(A\)
Cả điểm \(D\) và điểm \(B\)
Chọn câu sai.
Điểm \(B\) nằm giữa \(A\) và \(C.\)
Điểm \(B\) nằm giữa \(A\) và \(D.\)
Điểm \(C\) nằm giữa \(A\) và \(B.\)
Điểm \(C\) nằm giữa \(D\) và \(A.\)
Chọn câu đúng.
Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó không thẳng hàng
Nếu ba điểm không cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng
Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng
Cả ba đáp án trên đều sai.
Đáp án : C
Định nghĩa ba điểm thẳng hàng, không thẳng hàng:
+ Khi ba điểm cùng thuộc một đường thẳng, ta nói là ba điểm thẳng hàng.
+ Khi ba điểm không cùng thuộc bất kì đường thẳng nào, ta nói chúng không thẳng hàng.
Từ định nghĩa ba điểm thẳng hàng ta thấy đáp án C đúng.
Cho ba điểm \(M;N;P\) thẳng hàng với \(P\) nằm giữa \(M\) và \(N.\) Chọn hình vẽ đúng.




Đáp án : A
Xét từng đáp án:
- Kiểm tra xem ba điểm \(M,N,P\) có thẳng hàng hay không.
- Kiểm tra điểm \(P\) nằm giữa hai điểm \(M,N\)
Đáp án A: Ta thấy ba điểm \(M,N,P\) thẳng hàng và điểm \(P\) nằm giữa hai điểm \(M,N\) nên A đúng.
Đáp án B: Ta thấy ba điểm \(M,N,P\) thẳng hàng và điểm \(P\) không nằm giữa hai điểm \(M,N\) nên B sai.
Đáp án C: Ta thấy ba điểm \(M,N,P\) không thẳng hàng nên C sai.
Đáp án D: Ta thấy ba điểm \(M,N,P\) không thẳng hàng nên D sai.
Kể tên bộ ba điểm thẳng hàng trong hình vẽ dưới đây.

\(A,O,D\) và \(B,O,C\)
\(A,O,B\) và \(C,O,D\)
\(A,O,C\) và \(B,O,D\)
\(A,O,C\) và \(B,O,A\)
Đáp án : C
Ba điểm cùng thuộc một đường thẳng thì chúng thẳng hàng.
Các bộ ba điểm thẳng hàng trong hình vẽ là:
\(A,O,C\) và \(B,O,D\)
Có bao nhiêu bộ ba điểm thẳng hàng trên hình vẽ sau:

\(10\)
\(11\)
\(12\)
\(13\)
Đáp án : B
Tìm các bộ ba điểm thẳng hàng và kết luận.
Chú ý:
Ba điểm cùng thuộc một đường thẳng thì chúng thẳng hàng.
Các bộ ba điểm thẳng hàng trong hình vẽ là:
\(\left( {A,O,C} \right),\left( {B,O,D} \right),\left( {D,C,E} \right),\) \(\left( {B,H,C} \right),\left( {A,I,H} \right),\left( {A,I,E} \right),\) \(\left( {A,H,E} \right),\left( {I,H,E} \right),\left( {D,O,I} \right),\) \(\left( {D,I,B} \right),\left( {O,I,B} \right)\)
Vậy có tất cả \(11\) bộ ba điểm thẳng hàng trong hình vẽ.
Cho hình vẽ sau. Chọn câu sai.

Ba điểm \(D;E;B\) thẳng hàng
Ba điểm \(C;E;A\) không thẳng hàng
Ba điểm \(A;B;F\) thẳng hàng
Ba điểm \(D;E;F\) thẳng hàng
Đáp án : D
Quan sát hình vẽ, nhận xét tính đúng sai của từng đáp án, sử dungj định nghĩa ba điểm thẳng hàng: ba điểm cùng thuộc một đường thẳng thì chúng thẳng hàng.
Đáp án A: Ba điểm \(D,E,B\) thẳng hàng nên A đúng.
Đáp án B: Ba điểm \(C;E;A\) không thẳng hàng nên B đúng.
Đáp án C: Ba điểm \(A;B;F\) thẳng hàng nên C đúng.
Đáp án D: Ba điểm \(D;E;F\) không thẳng hàng nên D sai.
Có bao nhiêu bộ ba điểm thẳng hàng trong hình vẽ dưới đây?

\(7\)
\(4\)
\(5\)
\(6\)
Đáp án : B
Liệt kê các bộ ba điểm thẳng hàng trong hình vẽ và kết luận.
Các bộ ba điểm thẳng hàng trong hình vẽ là:
\(\left( {A,I,H} \right),\left( {B,I,K} \right),\) \(\left( {A,K,C} \right),\left( {B,H,C} \right).\)
Vậy có \(4\) cặp điểm thỏa mãn bài toán.
Có bao nhiêu bộ ba điểm không thẳng hàng trong hình vẽ sau

\(3\)
\(5\)
\(4\)
\(6\)
Đáp án : C
Liệt kê các bộ ba điểm không thẳng hàng và kết luận.
Các bộ ba điểm trong hình vẽ là:
\(\left( {M,N,P} \right),\left( {M,N,Q} \right),\) \(\left( {M,P,Q} \right),\left( {N,P,Q} \right)\)
Vậy có \(4\) bộ ba điểm không thẳng hàng.
Cho bốn điểm $M;N;P;Q$ cùng nằm trên một đường thẳng và hai điểm $M;N$ nằm cùng phía đối với điểm $Q$ còn hai điểm $N,P$ nằm khác phía đối với điểm $Q.$ Một hình vẽ đúng là:
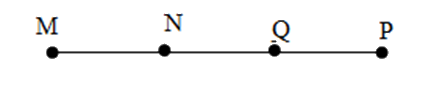


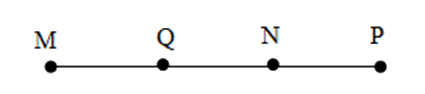
Đáp án : A
Quan sát hình vẽ ở các đáp án, đối chiếu với yêu cầu bài cho rồi kết luận
Đáp án A: Hai điểm \(M,N\) nằm cùng phía so với \(Q\) và hai điểm \(N,P\) khác phía so với \(Q\) nên thỏa mãn, chọn A.
Đáp án B: Hai điểm \(N,P\) cùng phía so với \(Q\) nên không thỏa mãn, loại B.
Đáp án C: Hai điểm \(N,P\) cùng phía so với \(Q\) nên không thỏa mãn, loại C.
Đáp án D: Hai điểm \(M,N\) nằm khác phía so với \(Q\) nên không thỏa mãn, loại D.
Cho $5$ điểm $A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D,{\rm{ }}O$ sao cho $3$ điểm $A,{\rm{ }}B,{\rm{ }}C$ cùng thuộc đường thẳng $d;$ $3$ điểm $B,{\rm{ }}C,{\rm{ }}D$ thẳng hàng và $3$ điểm $C,{\rm{ }}D,{\rm{ }}O$ không thẳng hàng. Hỏi điểm nào nằm ngoài đường thẳng $d?$
\(O,A\)
\(O\)
\(D\)
\(C,D\)
Đáp án : B
Vẽ hình theo yêu cầu bài toán và kết luận dựa vào định nghĩa ba diểm thẳng hàng:
Ba điểm cùng thuộc một đường thẳng thì chúng thẳng hàng hoặc ba điểm thẳng hàng thì cùng thuộc một đường thẳng.

Vì ba điểm \(A,B,C\) thuộc \(d\) và \(B,C,D\) thẳng hàng nên \(D \in d\)
Mà \(C,D \in d\) nên nếu \(C,D,O\) không thẳng hàng thì \(O \notin d\)
Vậy điểm \(O\) không thuộc đường thẳng \(d\)
Cho hình vẽ sau:

Kể tên các điểm nằm giữa \(A\) và \(D.\)
\(N,B,C\)
\(B,C,D\)
\(N\)
\(B,C\)
Đáp án: A
Quan sát hĩnh vẽ và tìm các điểm nằm giữa \(A\) và \(D\)
Các điểm nằm giữa \(A\) và \(D\) là \(N,B,C\)
Có bao nhiêu điểm nằm giữa \(N\) và \(D?\)
\(3\)
\(1\)
\(2\)
\(0\)
Đáp án: C
Tìm các điểm nằm giữa hai điểm \(N,D\) rồi kết luận.
Các điểm nằm giữa \(N\) và \(D\) là \(B,C\)
Vậy có \(2\) điểm cần tìm.
Số cặp điểm nằm cùng phía với điểm \(A\) là:
\(9\)
\(18\)
\(12\)
\(6\)
Đáp án: D
Liệt kê tất cả các cặp điểm nằm cùng phía với điểm \(A\)
Các cặp điểm nằm cùng phía so với điểm \(A\) là:
\(\left( {N,B} \right),\left( {N,C} \right),\left( {N,D} \right),\) \(\left( {B,C} \right),\left( {B,D} \right),\left( {C,D} \right)\)
Vậy có \(6\) cặp điểm thỏa mãn bài toán.
Trên hình vẽ, điểm \(B\) nằm giữa bao nhiêu cặp điểm?
\(10\)
\(8\)
\(4\)
\(6\)
Đáp án: C
Liệt kê các cặp điểm thỏa mãn điểm \(B\) nằm giữa.
Điểm \(B\) nằm giữa các cặp điểm là:
\(\left( {N,C} \right),\left( {A,D} \right),\left( {A,C} \right),\left( {N,D} \right)\)
Vậy có \(4\) cặp điểm thỏa mãn bài toán.
Cho hình vẽ sau:

Trên hình vẽ, điểm \(B\) và \(D\) nằm khác phía với mấy điểm?
\(0\)
\(3\)
\(4\)
\(1\)
Đáp án: D
Tìm số điểm nằm giữa hai điểm \(B,D\) trong hình vẽ rồi suy ra kết luận.
Sử dụng kiến thức: Nếu điểm \(B\) nằm giữa hai điểm \(A,C\) thì ta nói hai điểm \(A,C\) nằm khác phía so với \(B\).
Trong hình vẽ chỉ có điểm \(C\) nằm giữa hai điểm \(B\) và \(D\) nên chỉ có \(1\) điểm thỏa mãn yêu cầu bài toán.
Trên hình vẽ, điểm \(A\) và \(B\) nằm cùng phía với các điểm nào?
điểm \(C\)
điểm \(D\)
điểm \(B\)
Cả điểm \(C\) và điểm \(D\)
Đáp án: D
Sử dụng kiến thức: Nếu điểm \(B\) nằm giữa hai điểm \(A,C\) thì ta nói hai điểm \(A,B\) nằm cùng phía so với \(C\) và \(B,C\) nằm cùng phía so với \(A\).
Trên hình vẽ, hai điểm \(A,B\) nằm cùng phía so với các điểm \(C,D\).
Điểm \(A\) và \(C\) nằm cùng phía với điểm nào?
điểm \(D\)
điểm \(B\)
điểm \(A\)
Cả điểm \(D\) và điểm \(B\)
Đáp án: A
Sử dụng kiến thức: Nếu điểm \(B\) nằm giữa hai điểm \(A,C\) thì ta nói hai điểm \(A,B\) nằm cùng phía so với \(C\) và \(B,C\) nằm cùng phía so với \(A\).
Trên hình vẽ, hai điểm \(A,C\) nằm cùng phía so với điểm \(D\) và nằm khác phía so với điểm \(B\).
Chọn câu sai.
Điểm \(B\) nằm giữa \(A\) và \(C.\)
Điểm \(B\) nằm giữa \(A\) và \(D.\)
Điểm \(C\) nằm giữa \(A\) và \(B.\)
Điểm \(C\) nằm giữa \(D\) và \(A.\)
Đáp án: C
Quan sát hình vẽ và nhận xét tính đúng sai của từng đáp án.
Chú ý: Trong ba điểm thẳng hàng chỉ có \(1\) điểm nằm giữa hai điểm còn lại.
Đáp án A: Điểm \(B\) nằm giữa \(A\) và \(C\) nên A đúng và C sai.
Đáp án B: Điểm \(B\) nằm giữa \(A\) và \(D\) nên B đúng.
Điểm \(C\) nằm giữa \(D\) và \(A\) nên D đúng.
Bài 2 trong chương trình Toán 6 Chân trời sáng tạo tập trung vào việc làm quen với các khái niệm cơ bản trong hình học, đặc biệt là vị trí tương đối của ba điểm trên một đường thẳng. Việc nắm vững kiến thức này là nền tảng quan trọng cho các bài học hình học phức tạp hơn ở các lớp trên.
1. Ba điểm thẳng hàng: Ba điểm được gọi là thẳng hàng khi chúng cùng nằm trên một đường thẳng. Điều này có nghĩa là nếu nối hai trong ba điểm đó, đường thẳng đi qua cả ba điểm.
2. Ba điểm không thẳng hàng: Ba điểm được gọi là không thẳng hàng khi chúng không cùng nằm trên một đường thẳng. Khi đó, chúng tạo thành một tam giác.
3. Cách kiểm tra ba điểm thẳng hàng: Có nhiều cách để kiểm tra ba điểm A, B, C có thẳng hàng hay không:
1. Nhận biết ba điểm thẳng hàng, không thẳng hàng: Dạng bài tập này yêu cầu học sinh xác định xem ba điểm cho trước có thẳng hàng hay không dựa trên hình vẽ hoặc thông tin về vị trí của chúng.
Ví dụ: Cho ba điểm A, B, C. Điểm B nằm giữa A và C. Ba điểm A, B, C có thẳng hàng không?
2. Vận dụng định nghĩa để giải quyết bài toán: Dạng bài tập này yêu cầu học sinh sử dụng định nghĩa về ba điểm thẳng hàng, không thẳng hàng để giải quyết các bài toán thực tế.
Ví dụ: Cho tam giác ABC. Điểm D nằm trên cạnh BC. Ba điểm A, B, D có thẳng hàng không?
3. Bài tập kết hợp: Dạng bài tập này kết hợp kiến thức về ba điểm thẳng hàng, không thẳng hàng với các kiến thức khác trong chương trình Toán 6.
Dưới đây là một số bài tập trắc nghiệm để bạn luyện tập:
Việc nắm vững kiến thức về ba điểm thẳng hàng, ba điểm không thẳng hàng là rất quan trọng trong chương trình Toán 6. Hãy luyện tập thường xuyên với các bài tập trắc nghiệm để củng cố kiến thức và đạt kết quả tốt nhất. Giaitoan.edu.vn hy vọng với bộ đề trắc nghiệm này, các em học sinh sẽ tự tin hơn trong việc học tập và ôn luyện môn Toán.