Chào mừng các em học sinh lớp 6 đến với chuyên mục trắc nghiệm Hình chữ nhật - Hình thoi. Hình bình hành - Hình thang cân. Đây là cơ hội tuyệt vời để các em ôn tập lại kiến thức đã học, rèn luyện kỹ năng giải bài tập và chuẩn bị tốt nhất cho các kỳ kiểm tra sắp tới.
Tại giaitoan.edu.vn, chúng tôi cung cấp hệ thống câu hỏi trắc nghiệm đa dạng, bao gồm nhiều mức độ khó khác nhau, cùng với đáp án chi tiết và lời giải thích rõ ràng.
Trong những khẳng định sau, khẳng định nào sai?
Hình bình hành có hai cạnh đối song song.
Cho hình chữ nhật ABCD, phát biểu nào đúng?
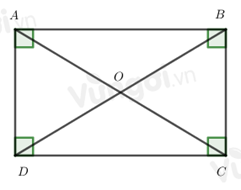
\(AC = BD\)

Độ dài đáy của hình bình hành có chiều cao \(24cm\) và diện tích là \(432c{m^2}\) là:
A. \(16cm\)
B. \(17cm\)
C. \(18cm\)
D. \(19cm\)
Chọn phát biểu sai trong các phát biểu sau?
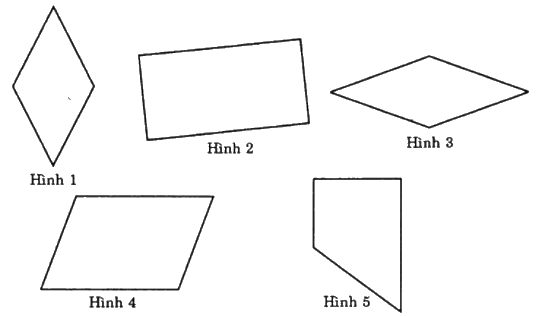
Trong các hình sau, các hình là hình thoi là:
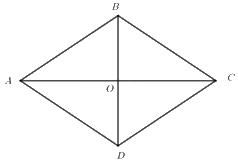
Cho hình thoi \(ABCD\) (\(AC > BD\)) có \(AC = 10\,\,\,cm\), khẳng định nào sau đây đúng:
Trong các hình dưới đây, hình nào là hình thang cân:


Điền số thích hợp vào ô trống:
Một bình hành có diện tích là \(8d{m^2}\) và độ dài cạnh đáy là \(32cm\).
Vậy chiều cao tương ứng với cạnh đáy đó là
\(cm\).
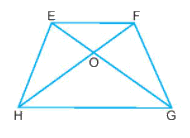
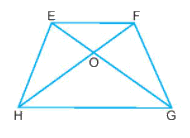
Quan sát hình thang cân EFGH, đoạn EG bằng đoạn:
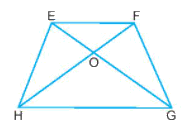
Tên các đỉnh của hình thang cân EFGH dưới đây là

Điền số thích hợp vào ô trống:
Một hình bình hành có diện tích là \(1855d{m^2}\) và độ dài cạnh đáy là \(53dm\).
Vậy chiều cao của hình bình hành đó là
\(dm\).
Hình thang cân có:
1 cạnh bên

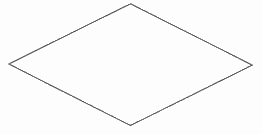
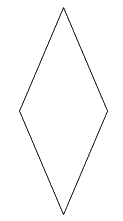
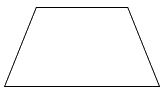
Trong các hình sau, hình nào là hình thoi?

Hình thang cân EFGH có:
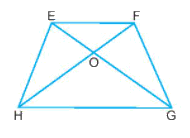
Quan sát hình thang cân EFGH, cạnh EH bằng?
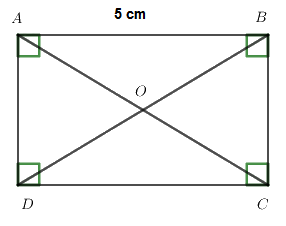
Cho hình chữ nhật ABCD, \(AB = 5cm\), chọn khẳng định đúng:
Chọn đáp án đúng hoặc sai cho mỗi khẳng định bên dưới:
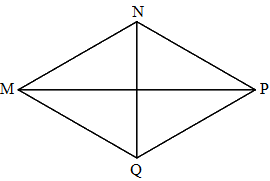
Trong hình thoi MNPQ:
MN và PQ không bằng nhau.
MN không song song với MQ
Các cặp cạnh đối diện song song.
MN = NP = PQ = QM
Chọn phát biểu sai?

Trong các hình sau, hình nào là hình bình hành?

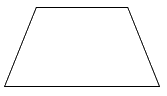
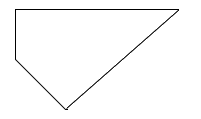
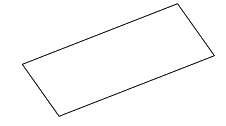
Trong các hình dưới đây, hình nào là hình bình hành?
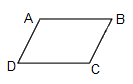
Cho hình bình hành \(ABCD\), cặp cạnh song song với nhau là:
Lời giải và đáp án
Trong những khẳng định sau, khẳng định nào sai?
Hình bình hành có hai cạnh đối song song.
Đáp án : C
Dựa vào cách nhận biết hình bình hành.
Hình bình hành có 4 đỉnh, có bốn cạnh, hai cạnh đối song song => A, B, D đúng
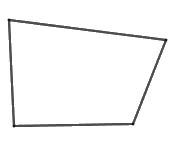
Hình có bốn đỉnh chưa chắc là hình bình hành, ví dụ:
Cho hình chữ nhật ABCD, phát biểu nào đúng?
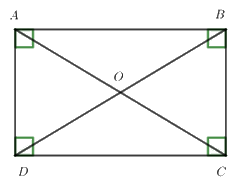
\(AC = BD\)
Đáp án : C
Trong hình chữ nhật hai đường chéo bằng nhau
Trong hình chữ nhật hai đường chéo bằng nhau nên \(AC = BD\) => Đáp án C đúng
Đáp án A sai do AB là cạnh, AC là đường chéo nên chúng không bằng nhau.
Đáp án B sai do AC là đường chéo, DO là một nửa đường chéo còn lại nên chúng không bằng nhau.
Đáp án D sai do OB là một nửa đường chéo, AC là đường chéo còn lại nên chúng không bằng nhau.

Độ dài đáy của hình bình hành có chiều cao \(24cm\) và diện tích là \(432c{m^2}\) là:
A. \(16cm\)
B. \(17cm\)
C. \(18cm\)
D. \(19cm\)
C. \(18cm\)
Từ công thức tính diện tích hình bình hành: \(S = a \times h\), ta có thể suy ra công thức tính độ dài cạnh đáy \(a\) là \(a = S:h\).
Độ dài đáy của hình bình hành đó là:
\(432:24 = 18\,\,(cm)\)
Đáp số: \(18cm\).
Chọn phát biểu sai trong các phát biểu sau?
Đáp án : D
Hình có bốn đỉnh chưa chắc là hình thoi, ví dụ:
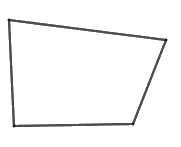
=> D sai
Trong các hình sau, các hình là hình thoi là:
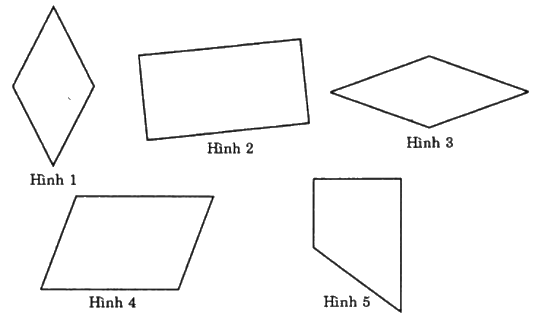
Đáp án : C
Hình thoi là hình tứ giác có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
Hình thoi là hình tứ giác có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
=> Hình 1 và Hình 3 là hình thoi
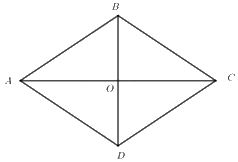
Cho hình thoi \(ABCD\) (\(AC > BD\)) có \(AC = 10\,\,\,cm\), khẳng định nào sau đây đúng:
Đáp án : B
Do hai đường chéo của hình thoi cắt nhau tại trung điểm của mỗi đường nên \(AO = OC = 10:2 = 5\,cm\)
=> B đúng, C sai
Vì \(BD < AC\) nên \(OB = OD < \frac{{10}}{2} = 5\,cm\).
=> A và C sai.
Trong các hình dưới đây, hình nào là hình thang cân:

Đáp án : B
Sử dụng dấu hiệu nhận biết hình thang cân.
Quan sát hình ta thấy Hình b là hình thang cân.

Điền số thích hợp vào ô trống:
Một bình hành có diện tích là \(8d{m^2}\) và độ dài cạnh đáy là \(32cm\).
Vậy chiều cao tương ứng với cạnh đáy đó là
\(cm\).
Một bình hành có diện tích là \(8d{m^2}\) và độ dài cạnh đáy là \(32cm\).
Vậy chiều cao tương ứng với cạnh đáy đó là
25\(cm\).
- Đổi \(8d{m^2}\) sang đơn vị đo là \(c{m^2}\).
- Từ công thức tính diện tích hình bình hành: \(S = a \times h\), ta có thể suy ra công thức tính chiều cao \(h\) là \(h = S\,:\,a\).
Đổi \(8d{m^2} = 800c{m^2}\)
Chiều cao của hình bình hành đó là:
\(800:32 = 25\,\,(cm)\)
Đáp số: \(25cm\).
Vậy đáp án đúng điền vào ô trống là \(25\).
Quan sát hình thang cân EFGH, đoạn EG bằng đoạn:
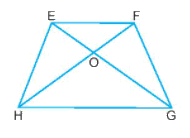
Đáp án : B
Sử dụng: Trong hình thang cân hai đường chéo bằng nhau.
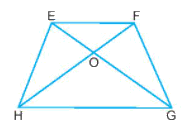
Do góc EG và HF là hai đường chéo của hình thang EFGH nên:
\(EG=HF\).
Tên các đỉnh của hình thang cân EFGH dưới đây là
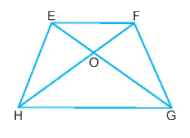
Đáp án : C
Sử dụng dấu hiệu nhận biết hình thang cân.
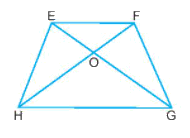
Hình thang cân EFGH có bốn đỉnh là: E, F, G, H.

Điền số thích hợp vào ô trống:
Một hình bình hành có diện tích là \(1855d{m^2}\) và độ dài cạnh đáy là \(53dm\).
Vậy chiều cao của hình bình hành đó là
\(dm\).
Một hình bình hành có diện tích là \(1855d{m^2}\) và độ dài cạnh đáy là \(53dm\).
Vậy chiều cao của hình bình hành đó là
35\(dm\).
Từ công thức tính diện tích hình bình hành: \(S = a \times h\), ta có thể suy ra công thức tính chiều cao \(h\) là \(h = S\,\,:\,\,a\).
Chiều cao của hình bình hành đó là:
\(1855:53 = 35\,\,(dm)\)
Đáp số: \(35dm\).
Vậy đáp án đúng điền vào ô trống là \(35\).
Hình thang cân có:
1 cạnh bên
Đáp án : B
Sử dụng dấu hiệu nhận biết hình thang cân.
Hình thang cân có 2 cạnh bên.

Trong các hình sau, hình nào là hình thoi?
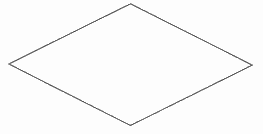
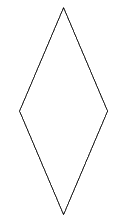
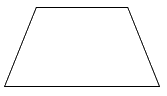

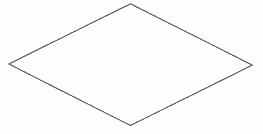
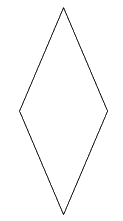
Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
Quan sát các hình đã cho ta thấy hình thứ nhất và thứ hai từ trên xuống là hình thoi.
Hình thứ ba là hình thang và hình thứ tư là hình bình hành.
Hình thang cân EFGH có:
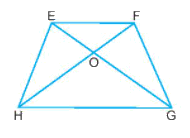
Đáp án : D
Sử dụng dấu hiệu nhận biết hình thang cân.
Hình thang cân EFGH có: EG và HF là đường chéo.
Quan sát hình thang cân EFGH, cạnh EH bằng?
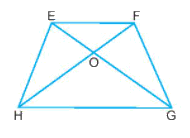
Đáp án : D
Sử dụng: Trong hình thang cân hai cạnh bên bằng nhau.
Do góc EH và FG là cạnh bên của hình thang EFGH nên:
\(EH=FG\)
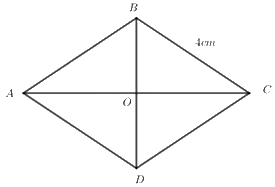
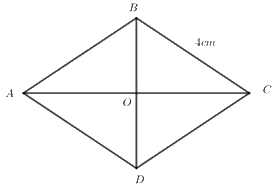
Đáp án : C
Hình thoi có bốn cạnh bằng nhau.
Hình thoi có bốn cạnh bằng nhau nên \(AB = BC = DC = AD = 4\,cm\).
=> \(DC = 4\,\,cm\).
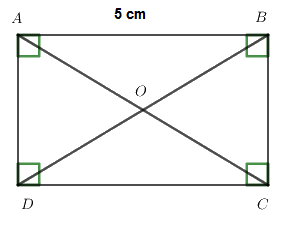
Cho hình chữ nhật ABCD, \(AB = 5cm\), chọn khẳng định đúng:
Đáp án : D
Trong hình chữ nhật hai cạnh đối bằng nhau.
Trong hình chữ nhật ABCD, cạnh đối của cạnh AB là DC nên \(AB = DC = 5\,cm\)
Chọn đáp án đúng hoặc sai cho mỗi khẳng định bên dưới:
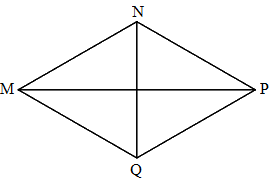
Trong hình thoi MNPQ:
MN và PQ không bằng nhau.
MN không song song với MQ
Các cặp cạnh đối diện song song.
MN = NP = PQ = QM
MN và PQ không bằng nhau.
MN không song song với MQ
Các cặp cạnh đối diện song song.
MN = NP = PQ = QM
Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
Trong hình thoi MNPQ ta có:
- Hai cặp cạnh đối diện song song: MN song song với PQ, NP song song với MQ.
- Bốn cạnh bằng nhau: MN = NP = PQ = QM.
Vậy các khẳng định đúng là b,c, d; khẳng định sai là a.
Chọn phát biểu sai?
Đáp án : A
Sử dụng dấu hiệu nhận biết hình chữ nhật
Hình chữ nhật có bốn đỉnh, hai cặp cạnh đối song song, hai đường chéo bằng nhau.
=> Đáp án B, C, D đúng.
Hình có 4 đỉnh chưa chắc là hình chữ nhật ví dụ:

Trong các hình sau, hình nào là hình bình hành?

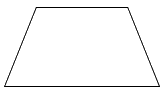
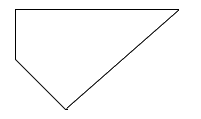
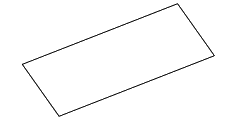

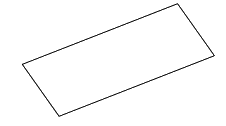
Quan sát các hình đã cho ta thấy hình thứ nhất và hình thứ tư từ trên xuống có hai cặp cạnh đối diện song song và bằng nhau nên các hình đó là hình bình hành.
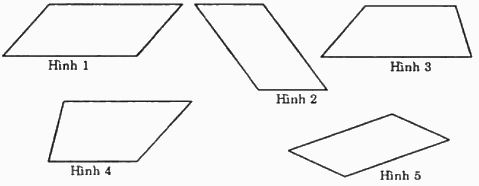
Trong các hình dưới đây, hình nào là hình bình hành?
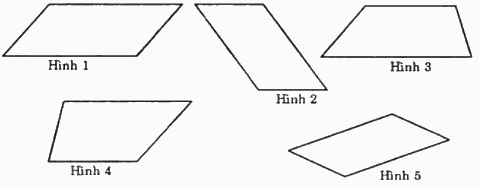
Đáp án : D
Hình bình hành là tứ giác có hai cặp cạnh đối diện song song và bằng nhau.
Các hình là hình bình hành là: Hình 1, hình 2, hình 5
Cho hình bình hành \(ABCD\), cặp cạnh song song với nhau là:
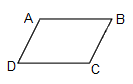
Đáp án : C
Trong hình bình hành hai cặp cạnh đối diện song song với nhau.
Vì trong hình bình hành hai cặp cạnh đối diện song song với nhau nên BC song song với AD
=> C đúng
Trong những khẳng định sau, khẳng định nào sai?
Hình bình hành có hai cạnh đối song song.
Cho hình chữ nhật ABCD, phát biểu nào đúng?

\(AC = BD\)

Độ dài đáy của hình bình hành có chiều cao \(24cm\) và diện tích là \(432c{m^2}\) là:
A. \(16cm\)
B. \(17cm\)
C. \(18cm\)
D. \(19cm\)
Chọn phát biểu sai trong các phát biểu sau?
Trong các hình sau, các hình là hình thoi là:


Cho hình thoi \(ABCD\) (\(AC > BD\)) có \(AC = 10\,\,\,cm\), khẳng định nào sau đây đúng:
Trong các hình dưới đây, hình nào là hình thang cân:


Điền số thích hợp vào ô trống:
Một bình hành có diện tích là \(8d{m^2}\) và độ dài cạnh đáy là \(32cm\).
Vậy chiều cao tương ứng với cạnh đáy đó là
\(cm\).
Quan sát hình thang cân EFGH, đoạn EG bằng đoạn:

Tên các đỉnh của hình thang cân EFGH dưới đây là


Điền số thích hợp vào ô trống:
Một hình bình hành có diện tích là \(1855d{m^2}\) và độ dài cạnh đáy là \(53dm\).
Vậy chiều cao của hình bình hành đó là
\(dm\).
Hình thang cân có:
1 cạnh bên

Trong các hình sau, hình nào là hình thoi?




Hình thang cân EFGH có:

Quan sát hình thang cân EFGH, cạnh EH bằng?



Cho hình chữ nhật ABCD, \(AB = 5cm\), chọn khẳng định đúng:
Chọn đáp án đúng hoặc sai cho mỗi khẳng định bên dưới:

Trong hình thoi MNPQ:
MN và PQ không bằng nhau.
MN không song song với MQ
Các cặp cạnh đối diện song song.
MN = NP = PQ = QM
Chọn phát biểu sai?

Trong các hình sau, hình nào là hình bình hành?




Trong các hình dưới đây, hình nào là hình bình hành?

Cho hình bình hành \(ABCD\), cặp cạnh song song với nhau là:

Trong những khẳng định sau, khẳng định nào sai?
Hình bình hành có hai cạnh đối song song.
Đáp án : C
Dựa vào cách nhận biết hình bình hành.
Hình bình hành có 4 đỉnh, có bốn cạnh, hai cạnh đối song song => A, B, D đúng
Hình có bốn đỉnh chưa chắc là hình bình hành, ví dụ:

Cho hình chữ nhật ABCD, phát biểu nào đúng?

\(AC = BD\)
Đáp án : C
Trong hình chữ nhật hai đường chéo bằng nhau
Trong hình chữ nhật hai đường chéo bằng nhau nên \(AC = BD\) => Đáp án C đúng
Đáp án A sai do AB là cạnh, AC là đường chéo nên chúng không bằng nhau.
Đáp án B sai do AC là đường chéo, DO là một nửa đường chéo còn lại nên chúng không bằng nhau.
Đáp án D sai do OB là một nửa đường chéo, AC là đường chéo còn lại nên chúng không bằng nhau.

Độ dài đáy của hình bình hành có chiều cao \(24cm\) và diện tích là \(432c{m^2}\) là:
A. \(16cm\)
B. \(17cm\)
C. \(18cm\)
D. \(19cm\)
C. \(18cm\)
Từ công thức tính diện tích hình bình hành: \(S = a \times h\), ta có thể suy ra công thức tính độ dài cạnh đáy \(a\) là \(a = S:h\).
Độ dài đáy của hình bình hành đó là:
\(432:24 = 18\,\,(cm)\)
Đáp số: \(18cm\).
Chọn phát biểu sai trong các phát biểu sau?
Đáp án : D
Hình có bốn đỉnh chưa chắc là hình thoi, ví dụ:

=> D sai
Trong các hình sau, các hình là hình thoi là:

Đáp án : C
Hình thoi là hình tứ giác có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
Hình thoi là hình tứ giác có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
=> Hình 1 và Hình 3 là hình thoi

Cho hình thoi \(ABCD\) (\(AC > BD\)) có \(AC = 10\,\,\,cm\), khẳng định nào sau đây đúng:
Đáp án : B
Do hai đường chéo của hình thoi cắt nhau tại trung điểm của mỗi đường nên \(AO = OC = 10:2 = 5\,cm\)
=> B đúng, C sai
Vì \(BD < AC\) nên \(OB = OD < \frac{{10}}{2} = 5\,cm\).
=> A và C sai.
Trong các hình dưới đây, hình nào là hình thang cân:

Đáp án : B
Sử dụng dấu hiệu nhận biết hình thang cân.
Quan sát hình ta thấy Hình b là hình thang cân.

Điền số thích hợp vào ô trống:
Một bình hành có diện tích là \(8d{m^2}\) và độ dài cạnh đáy là \(32cm\).
Vậy chiều cao tương ứng với cạnh đáy đó là
\(cm\).
Một bình hành có diện tích là \(8d{m^2}\) và độ dài cạnh đáy là \(32cm\).
Vậy chiều cao tương ứng với cạnh đáy đó là
25\(cm\).
- Đổi \(8d{m^2}\) sang đơn vị đo là \(c{m^2}\).
- Từ công thức tính diện tích hình bình hành: \(S = a \times h\), ta có thể suy ra công thức tính chiều cao \(h\) là \(h = S\,:\,a\).
Đổi \(8d{m^2} = 800c{m^2}\)
Chiều cao của hình bình hành đó là:
\(800:32 = 25\,\,(cm)\)
Đáp số: \(25cm\).
Vậy đáp án đúng điền vào ô trống là \(25\).
Quan sát hình thang cân EFGH, đoạn EG bằng đoạn:

Đáp án : B
Sử dụng: Trong hình thang cân hai đường chéo bằng nhau.

Do góc EG và HF là hai đường chéo của hình thang EFGH nên:
\(EG=HF\).
Tên các đỉnh của hình thang cân EFGH dưới đây là

Đáp án : C
Sử dụng dấu hiệu nhận biết hình thang cân.

Hình thang cân EFGH có bốn đỉnh là: E, F, G, H.

Điền số thích hợp vào ô trống:
Một hình bình hành có diện tích là \(1855d{m^2}\) và độ dài cạnh đáy là \(53dm\).
Vậy chiều cao của hình bình hành đó là
\(dm\).
Một hình bình hành có diện tích là \(1855d{m^2}\) và độ dài cạnh đáy là \(53dm\).
Vậy chiều cao của hình bình hành đó là
35\(dm\).
Từ công thức tính diện tích hình bình hành: \(S = a \times h\), ta có thể suy ra công thức tính chiều cao \(h\) là \(h = S\,\,:\,\,a\).
Chiều cao của hình bình hành đó là:
\(1855:53 = 35\,\,(dm)\)
Đáp số: \(35dm\).
Vậy đáp án đúng điền vào ô trống là \(35\).
Hình thang cân có:
1 cạnh bên
Đáp án : B
Sử dụng dấu hiệu nhận biết hình thang cân.
Hình thang cân có 2 cạnh bên.

Trong các hình sau, hình nào là hình thoi?






Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
Quan sát các hình đã cho ta thấy hình thứ nhất và thứ hai từ trên xuống là hình thoi.
Hình thứ ba là hình thang và hình thứ tư là hình bình hành.
Hình thang cân EFGH có:

Đáp án : D
Sử dụng dấu hiệu nhận biết hình thang cân.
Hình thang cân EFGH có: EG và HF là đường chéo.
Quan sát hình thang cân EFGH, cạnh EH bằng?

Đáp án : D
Sử dụng: Trong hình thang cân hai cạnh bên bằng nhau.
Do góc EH và FG là cạnh bên của hình thang EFGH nên:
\(EH=FG\)

Đáp án : C
Hình thoi có bốn cạnh bằng nhau.
Hình thoi có bốn cạnh bằng nhau nên \(AB = BC = DC = AD = 4\,cm\).
=> \(DC = 4\,\,cm\).

Cho hình chữ nhật ABCD, \(AB = 5cm\), chọn khẳng định đúng:
Đáp án : D
Trong hình chữ nhật hai cạnh đối bằng nhau.
Trong hình chữ nhật ABCD, cạnh đối của cạnh AB là DC nên \(AB = DC = 5\,cm\)
Chọn đáp án đúng hoặc sai cho mỗi khẳng định bên dưới:

Trong hình thoi MNPQ:
MN và PQ không bằng nhau.
MN không song song với MQ
Các cặp cạnh đối diện song song.
MN = NP = PQ = QM
MN và PQ không bằng nhau.
MN không song song với MQ
Các cặp cạnh đối diện song song.
MN = NP = PQ = QM
Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
Trong hình thoi MNPQ ta có:
- Hai cặp cạnh đối diện song song: MN song song với PQ, NP song song với MQ.
- Bốn cạnh bằng nhau: MN = NP = PQ = QM.
Vậy các khẳng định đúng là b,c, d; khẳng định sai là a.
Chọn phát biểu sai?
Đáp án : A
Sử dụng dấu hiệu nhận biết hình chữ nhật
Hình chữ nhật có bốn đỉnh, hai cặp cạnh đối song song, hai đường chéo bằng nhau.
=> Đáp án B, C, D đúng.
Hình có 4 đỉnh chưa chắc là hình chữ nhật ví dụ:


Trong các hình sau, hình nào là hình bình hành?






Quan sát các hình đã cho ta thấy hình thứ nhất và hình thứ tư từ trên xuống có hai cặp cạnh đối diện song song và bằng nhau nên các hình đó là hình bình hành.
Trong các hình dưới đây, hình nào là hình bình hành?

Đáp án : D
Hình bình hành là tứ giác có hai cặp cạnh đối diện song song và bằng nhau.
Các hình là hình bình hành là: Hình 1, hình 2, hình 5
Cho hình bình hành \(ABCD\), cặp cạnh song song với nhau là:

Đáp án : C
Trong hình bình hành hai cặp cạnh đối diện song song với nhau.
Vì trong hình bình hành hai cặp cạnh đối diện song song với nhau nên BC song song với AD
=> C đúng
Chương trình Toán 6 Chân trời sáng tạo đi sâu vào các kiến thức cơ bản về hình học, đặc biệt là các loại tứ giác. Việc nắm vững đặc điểm, tính chất của từng loại tứ giác là nền tảng quan trọng để giải quyết các bài toán liên quan. Bài viết này sẽ cung cấp một loạt các trắc nghiệm về Hình chữ nhật, Hình thoi, Hình bình hành và Hình thang cân, giúp học sinh củng cố kiến thức và rèn luyện kỹ năng.
Hình chữ nhật là tứ giác có bốn góc vuông. Các tính chất quan trọng của hình chữ nhật bao gồm:
Các dạng bài tập thường gặp về hình chữ nhật:
Hình thoi là tứ giác có bốn cạnh bằng nhau. Các tính chất quan trọng của hình thoi bao gồm:
Các dạng bài tập thường gặp về hình thoi:
Hình bình hành là tứ giác có các cạnh đối song song. Các tính chất quan trọng của hình bình hành bao gồm:
Các dạng bài tập thường gặp về hình bình hành:
Hình thang cân là hình thang có hai cạnh bên bằng nhau. Các tính chất quan trọng của hình thang cân bao gồm:
Các dạng bài tập thường gặp về hình thang cân:
Dưới đây là một số ví dụ về các câu hỏi trắc nghiệm về các loại tứ giác:
Hy vọng với những kiến thức và bài tập trắc nghiệm trên, các em học sinh sẽ tự tin hơn trong việc học tập và ôn luyện môn Toán lớp 6 Chân trời sáng tạo. Chúc các em học tốt!