Chào mừng các em học sinh đến với bài trắc nghiệm Toán 6 Bài 5: Trung điểm của đoạn thẳng, thuộc chương trình Chân trời sáng tạo. Bài trắc nghiệm này được thiết kế để giúp các em ôn luyện và củng cố kiến thức về trung điểm của đoạn thẳng một cách hiệu quả.
Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm đa dạng, bao gồm các câu hỏi từ dễ đến khó, giúp các em tự đánh giá năng lực và chuẩn bị tốt nhất cho các bài kiểm tra trên lớp.
$M$ là trung điểm của đoạn thẳng $AB$ khi và chỉ khi:
$MA = MB$
\(AM = \dfrac{1}{2}AB\)
\(MA + MB = AB\)
$MA + MB = AB$ và $MA = MB$
Nếu ta có \(P\) là trung điểm của \(MN\) thì
\(MP = NP = \dfrac{{MN}}{2}\)
\(MP + NP = 2MN\)
\(MP = NP = \dfrac{{MN}}{4}\)
\(MP = NP = MN\)
Cho đoạn thẳng $AB$ dài $12cm$, $M$ là trung điểm của đoạn thẳng $AB.$ Khi đó, độ dài của đoạn thẳng $MA$ bằng
$3cm$
$15cm$
$6cm$
$20cm$
Cho $I$ là trung điểm của đoạn thẳng $MN.$ Biết $NI = 8cm$. Khi đó, độ dài của đoạn thẳng $MN$ bằng
$4cm$
$16cm$
$21cm$
$24cm$
Trên tia $Ox$ lấy hai điểm $A$ và $B$ sao cho $OA = 3cm,OB = 6cm$. Chọn câu sai.
Điểm \(A\) nằm giữa hai điểm \(O\) và \(B\)
Điểm \(A\) là trung điểm đoạn \(OB\)
Điểm \(O\) là trung điểm đoạn \(AB\)
\(OA = AB = 3cm\)
Cho đoạn thẳng $AB.$Gọi $M$ và $N$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AM.$ Giả sử $AN = 1,5cm$. Đoạn thẳng $AB$ có độ dài là?
$1,5cm$
$3cm$
$4,5cm$
$6cm$
Cho đoạn thẳng $AB = 8cm$. Gọi $I$ và $K$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AI.$ Đoạn thẳng $IK$ có độ dài là?
$8cm$
$4cm$
$2cm$
$6cm$
Trên tia $Ox$ lấy các điểm $M,{\rm{ }}N$ sao cho $OM = 2cm;ON = 3cm.$Trên tia đối của tia $NO$ lấy điểm $P$ sao cho $NP = 1cm.$
Tính độ dài các đoạn thẳng $MN$ và $MP.$
$MN = 1cm;\,MP = 3cm$
$MN = 2cm;\,MP = 3cm$
$MN = 2cm;\,MP = 1cm$
$MN = 1cm;\,MP = 2cm$
Hãy chọn câu đúng nhất
$N$ là trung điểm của đoạn thẳng $MP.$
$M$ là trung điểm của đoạn thẳng $OP.$
$M$ là trung điểm của đoạn thẳng $NP. $
Cả A, B đều đúng.
Cho đoạn thẳng $AB$ dài $14cm.$ Trên tia $AB$ lấy điểm $M$ sao cho $AM = 7cm.$ Chọn câu sai.
\(M\) nằm giữa \(A\) và \(B.\)
\(AM = BM = 7\,cm\)
\(BM = AB\)
\(M\) là trung điểm của \(AB.\)
Trên tia $Ox$ có các điểm $A,{\rm{ }}B$ sao cho $OA = 2cm;OB = 5cm.$ Gọi $M$ là trung điểm của đoạn thẳng $OB.$ Tính độ dài đoạn thẳng $AM.$
$AM = 1,5cm.$
$AM = 0,5cm.$
$AM = 1cm.$
$AM = 2cm.$
Lời giải và đáp án
$M$ là trung điểm của đoạn thẳng $AB$ khi và chỉ khi:
$MA = MB$
\(AM = \dfrac{1}{2}AB\)
\(MA + MB = AB\)
$MA + MB = AB$ và $MA = MB$
Đáp án : D
\(M\) là trung điểm của đoạn thẳng \(AB\)$ \Leftrightarrow \left\{ \begin{array}{l}AM + MB = AB\\{\rm{MA = MB}}\end{array} \right.$
Nếu ta có \(P\) là trung điểm của \(MN\) thì
\(MP = NP = \dfrac{{MN}}{2}\)
\(MP + NP = 2MN\)
\(MP = NP = \dfrac{{MN}}{4}\)
\(MP = NP = MN\)
Đáp án : A
Ta có \(P\) là trung điểm của \(MN\) thì \(MP = NP = \dfrac{{MN}}{2}\)
Cho đoạn thẳng $AB$ dài $12cm$, $M$ là trung điểm của đoạn thẳng $AB.$ Khi đó, độ dài của đoạn thẳng $MA$ bằng
$3cm$
$15cm$
$6cm$
$20cm$
Đáp án : C
Sử dụng kiến thức \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$
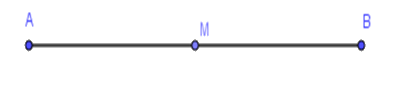
Vì \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = }}\dfrac{1}{2}AB = \dfrac{1}{2}.12 = 6cm$
Vậy $AM = 6cm$.
Cho $I$ là trung điểm của đoạn thẳng $MN.$ Biết $NI = 8cm$. Khi đó, độ dài của đoạn thẳng $MN$ bằng
$4cm$
$16cm$
$21cm$
$24cm$
Đáp án : B
Sử dụng kiến thức \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$
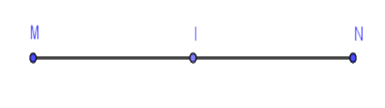
Vì $I$ là trung điểm của đoạn thẳng $MN$ nên $IM = IN = \dfrac{1}{2}MN$ hay $MN = 2.IN = 2.8 = 16cm$.
Trên tia $Ox$ lấy hai điểm $A$ và $B$ sao cho $OA = 3cm,OB = 6cm$. Chọn câu sai.
Điểm \(A\) nằm giữa hai điểm \(O\) và \(B\)
Điểm \(A\) là trung điểm đoạn \(OB\)
Điểm \(O\) là trung điểm đoạn \(AB\)
\(OA = AB = 3cm\)
Đáp án : C
+ Sử dụng kiến thức về điểm nằm giữa hai điểm
+ Sử dụng kiến thức về trung điểm đoạn thẳng
\(M\) là trung điểm của đoạn thẳng \(AB\)
$\Leftrightarrow $${\rm{MA = MB}}$ và \(M\) nằm giữa hai điểm \(A;B.\)

Vì hai điểm $A,B$ cùng thuộc tia $Ox$ mà $OA < OB\,\left( {3cm < 6cm} \right)$ nên điểm $A$ nằm giữa hai điểm $O$ và $B$. (1)
Do đó $OA + AB = OB$$ \Rightarrow AB = OB - OA = 6 - 3 = 3cm$. Suy ra $OA = AB = 3cm$(2)
Từ (1) và (2) suy ra $A$ là trung điểm của đoạn $OB$.
Vậy các đáp án $A;B;D$ đều đúng, $C$ sai.
Cho đoạn thẳng $AB.$Gọi $M$ và $N$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AM.$ Giả sử $AN = 1,5cm$. Đoạn thẳng $AB$ có độ dài là?
$1,5cm$
$3cm$
$4,5cm$
$6cm$
Đáp án : D
Sử dụng kiến thức về trung điểm đoạn thẳng : “\(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$” để tính toán.
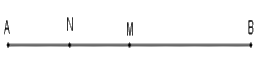
Vì $N$ là trung điểm đoạn $AM$ nên $AN = \dfrac{1}{2}AM$ hay $AM = 2AN = 2.1,5 = 3cm$
Lại có điểm $M$ là trung điểm đoạn thẳng $AB$ nên ta có $AM = \dfrac{1}{2}AB$ hay $AB = 2AM = 2.3 = 6cm$
Vậy $AB = 6cm$.
Cho đoạn thẳng $AB = 8cm$. Gọi $I$ và $K$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AI.$ Đoạn thẳng $IK$ có độ dài là?
$8cm$
$4cm$
$2cm$
$6cm$
Đáp án : C
Sử dụng kiến thức về trung điểm đoạn thẳng : “\(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$” để tính toán.
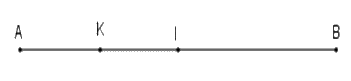
Vì điểm $I$ là trung điểm đoạn thẳng $AB$ nên $AI = \dfrac{1}{2}AB = \dfrac{1}{2}.8 = 4cm$
Vì điểm $K$ là trung điểm đoạn thẳng $AI$ nên $AK = \dfrac{1}{2}AI = \dfrac{1}{2}.4 = 2cm$
Vậy $AI = 2cm$.
Trên tia $Ox$ lấy các điểm $M,{\rm{ }}N$ sao cho $OM = 2cm;ON = 3cm.$Trên tia đối của tia $NO$ lấy điểm $P$ sao cho $NP = 1cm.$
Tính độ dài các đoạn thẳng $MN$ và $MP.$
$MN = 1cm;\,MP = 3cm$
$MN = 2cm;\,MP = 3cm$
$MN = 2cm;\,MP = 1cm$
$MN = 1cm;\,MP = 2cm$
Đáp án: D
Sử dụng công thức cộng đoạn thẳng để tính độ dài các đoạn thẳng.

Vì hai điểm $M;N$ cùng thuộc tia $Ox$ mà $OM < ON\left( {2cm < 3cm} \right)$ nên điểm $M$ nằm giữa hai điểm $O$ và $N$.
Do đó $OM + MN = ON \Rightarrow MN = ON - OM$ $ = 3 - 2 = 1cm$
Vì hai tia $NP$ và $NO$ đối nhau mà $M$ nằm giữa hai điểm $O$ và $N$ nên $N$ là điểm nằm giữa $M$ và $P$
Do đó $MN + NP = MP$ hay $MP = 1 + 1 = 2cm$.
Vậy $MN = 1cm;\,MP = 2cm$.
Hãy chọn câu đúng nhất
$N$ là trung điểm của đoạn thẳng $MP.$
$M$ là trung điểm của đoạn thẳng $OP.$
$M$ là trung điểm của đoạn thẳng $NP. $
Cả A, B đều đúng.
Đáp án: D
Ta sử dụng kiến thức sau:
Nếu \(M\) nằm giữa \(A\) và \(B\) đồng thời \(MA = MB\) thì \(M\) là trung điểm của \(AB.\)

Từ câu trước và đề bài ta có $MN = 1cm;\,MP = 2cm;\,OM = 2cm;NP = 1cm$
Suy ra $MN = NP\left( { = 1cm} \right)\,\,\,\left( 1 \right);\,MP = OM\left( { = 2cm} \right)\,\left( 2 \right)$
Lại có $M$ nằm giữa hai điểm $O$ và $N$ mà $N$ nằm giữa hai điểm $M$ và $P$ nên điểm $M$ nằm giữa hai điểm $O$ và $P$ (3)
Từ (2) và (3) ta có $M$ là trung điểm đoạn $OP.$
Theo câu trước ta có $N$ là điểm nằm giữa $M$ và $P$ nên kết hợp với $\left( 1 \right)$ suy ra $N$ là trung điểm đoạn $MP$.
Nên cả A, B đều đúng.
Cho đoạn thẳng $AB$ dài $14cm.$ Trên tia $AB$ lấy điểm $M$ sao cho $AM = 7cm.$ Chọn câu sai.
\(M\) nằm giữa \(A\) và \(B.\)
\(AM = BM = 7\,cm\)
\(BM = AB\)
\(M\) là trung điểm của \(AB.\)
Đáp án : C
Sử dụng kiến thức về điểm nằm giữa hai điểm và trung điểm của đoạn thẳng: “ Nếu \(M\) nằm giữa \(A\) và \(B\) đồng thời \(MA = MB\) thì \(M\) là trung điểm của \(AB.\)”
Vì điểm $M$ thuộc tia $AB$ mà $AM < AB\left( {7cm < 14cm} \right)$ nên điểm $M$ nằm giữa hai điểm $A$ và $B$. (1)
Do đó $AM + MB = AB$ $ \Rightarrow MB = AB - AM = 14 - 7 = 7cm$. Suy ra $AM = MB = 7cm$ (2)
Từ (1) và (2) suy ra $M$ là trung điểm của đoạn $AB$.
Vậy các đáp án A, B, D đúng và C sai vì $BM = 7cm < 14cm = AB$.
Trên tia $Ox$ có các điểm $A,{\rm{ }}B$ sao cho $OA = 2cm;OB = 5cm.$ Gọi $M$ là trung điểm của đoạn thẳng $OB.$ Tính độ dài đoạn thẳng $AM.$
$AM = 1,5cm.$
$AM = 0,5cm.$
$AM = 1cm.$
$AM = 2cm.$
Đáp án : B
+ Sử dụng tính chất trung điểm của đoạn thẳng: “\(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$” để tính đoạn $OM$.
+ Sử dụng công thức cộng đoạn thẳng để tính đoạn $AM$.

Vì $M$ là trung điểm của đoạn thẳng $OB$ nên ta có $OM = \dfrac{1}{2}OB = \dfrac{1}{2}.5 = 2,5cm$
Vì $A$ và $M$ cùng thuộc tia $Ox$ mà $OA < OM\,\left( {2cm < 2,5cm} \right)$ nên điểm $A$ nằm giữa hai điểm $O$ và $M$.
Do đó $OA + AM = OM$ $ \Rightarrow AM = OM - OA = 2,5 - 2 = 0,5cm$
Vậy $AM = 0,5cm.$
$M$ là trung điểm của đoạn thẳng $AB$ khi và chỉ khi:
$MA = MB$
\(AM = \dfrac{1}{2}AB\)
\(MA + MB = AB\)
$MA + MB = AB$ và $MA = MB$
Nếu ta có \(P\) là trung điểm của \(MN\) thì
\(MP = NP = \dfrac{{MN}}{2}\)
\(MP + NP = 2MN\)
\(MP = NP = \dfrac{{MN}}{4}\)
\(MP = NP = MN\)
Cho đoạn thẳng $AB$ dài $12cm$, $M$ là trung điểm của đoạn thẳng $AB.$ Khi đó, độ dài của đoạn thẳng $MA$ bằng
$3cm$
$15cm$
$6cm$
$20cm$
Cho $I$ là trung điểm của đoạn thẳng $MN.$ Biết $NI = 8cm$. Khi đó, độ dài của đoạn thẳng $MN$ bằng
$4cm$
$16cm$
$21cm$
$24cm$
Trên tia $Ox$ lấy hai điểm $A$ và $B$ sao cho $OA = 3cm,OB = 6cm$. Chọn câu sai.
Điểm \(A\) nằm giữa hai điểm \(O\) và \(B\)
Điểm \(A\) là trung điểm đoạn \(OB\)
Điểm \(O\) là trung điểm đoạn \(AB\)
\(OA = AB = 3cm\)
Cho đoạn thẳng $AB.$Gọi $M$ và $N$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AM.$ Giả sử $AN = 1,5cm$. Đoạn thẳng $AB$ có độ dài là?
$1,5cm$
$3cm$
$4,5cm$
$6cm$
Cho đoạn thẳng $AB = 8cm$. Gọi $I$ và $K$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AI.$ Đoạn thẳng $IK$ có độ dài là?
$8cm$
$4cm$
$2cm$
$6cm$
Trên tia $Ox$ lấy các điểm $M,{\rm{ }}N$ sao cho $OM = 2cm;ON = 3cm.$Trên tia đối của tia $NO$ lấy điểm $P$ sao cho $NP = 1cm.$
Tính độ dài các đoạn thẳng $MN$ và $MP.$
$MN = 1cm;\,MP = 3cm$
$MN = 2cm;\,MP = 3cm$
$MN = 2cm;\,MP = 1cm$
$MN = 1cm;\,MP = 2cm$
Hãy chọn câu đúng nhất
$N$ là trung điểm của đoạn thẳng $MP.$
$M$ là trung điểm của đoạn thẳng $OP.$
$M$ là trung điểm của đoạn thẳng $NP. $
Cả A, B đều đúng.
Cho đoạn thẳng $AB$ dài $14cm.$ Trên tia $AB$ lấy điểm $M$ sao cho $AM = 7cm.$ Chọn câu sai.
\(M\) nằm giữa \(A\) và \(B.\)
\(AM = BM = 7\,cm\)
\(BM = AB\)
\(M\) là trung điểm của \(AB.\)
Trên tia $Ox$ có các điểm $A,{\rm{ }}B$ sao cho $OA = 2cm;OB = 5cm.$ Gọi $M$ là trung điểm của đoạn thẳng $OB.$ Tính độ dài đoạn thẳng $AM.$
$AM = 1,5cm.$
$AM = 0,5cm.$
$AM = 1cm.$
$AM = 2cm.$
$M$ là trung điểm của đoạn thẳng $AB$ khi và chỉ khi:
$MA = MB$
\(AM = \dfrac{1}{2}AB\)
\(MA + MB = AB\)
$MA + MB = AB$ và $MA = MB$
Đáp án : D
\(M\) là trung điểm của đoạn thẳng \(AB\)$ \Leftrightarrow \left\{ \begin{array}{l}AM + MB = AB\\{\rm{MA = MB}}\end{array} \right.$
Nếu ta có \(P\) là trung điểm của \(MN\) thì
\(MP = NP = \dfrac{{MN}}{2}\)
\(MP + NP = 2MN\)
\(MP = NP = \dfrac{{MN}}{4}\)
\(MP = NP = MN\)
Đáp án : A
Ta có \(P\) là trung điểm của \(MN\) thì \(MP = NP = \dfrac{{MN}}{2}\)
Cho đoạn thẳng $AB$ dài $12cm$, $M$ là trung điểm của đoạn thẳng $AB.$ Khi đó, độ dài của đoạn thẳng $MA$ bằng
$3cm$
$15cm$
$6cm$
$20cm$
Đáp án : C
Sử dụng kiến thức \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$

Vì \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = }}\dfrac{1}{2}AB = \dfrac{1}{2}.12 = 6cm$
Vậy $AM = 6cm$.
Cho $I$ là trung điểm của đoạn thẳng $MN.$ Biết $NI = 8cm$. Khi đó, độ dài của đoạn thẳng $MN$ bằng
$4cm$
$16cm$
$21cm$
$24cm$
Đáp án : B
Sử dụng kiến thức \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$

Vì $I$ là trung điểm của đoạn thẳng $MN$ nên $IM = IN = \dfrac{1}{2}MN$ hay $MN = 2.IN = 2.8 = 16cm$.
Trên tia $Ox$ lấy hai điểm $A$ và $B$ sao cho $OA = 3cm,OB = 6cm$. Chọn câu sai.
Điểm \(A\) nằm giữa hai điểm \(O\) và \(B\)
Điểm \(A\) là trung điểm đoạn \(OB\)
Điểm \(O\) là trung điểm đoạn \(AB\)
\(OA = AB = 3cm\)
Đáp án : C
+ Sử dụng kiến thức về điểm nằm giữa hai điểm
+ Sử dụng kiến thức về trung điểm đoạn thẳng
\(M\) là trung điểm của đoạn thẳng \(AB\)
$\Leftrightarrow $${\rm{MA = MB}}$ và \(M\) nằm giữa hai điểm \(A;B.\)

Vì hai điểm $A,B$ cùng thuộc tia $Ox$ mà $OA < OB\,\left( {3cm < 6cm} \right)$ nên điểm $A$ nằm giữa hai điểm $O$ và $B$. (1)
Do đó $OA + AB = OB$$ \Rightarrow AB = OB - OA = 6 - 3 = 3cm$. Suy ra $OA = AB = 3cm$(2)
Từ (1) và (2) suy ra $A$ là trung điểm của đoạn $OB$.
Vậy các đáp án $A;B;D$ đều đúng, $C$ sai.
Cho đoạn thẳng $AB.$Gọi $M$ và $N$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AM.$ Giả sử $AN = 1,5cm$. Đoạn thẳng $AB$ có độ dài là?
$1,5cm$
$3cm$
$4,5cm$
$6cm$
Đáp án : D
Sử dụng kiến thức về trung điểm đoạn thẳng : “\(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$” để tính toán.

Vì $N$ là trung điểm đoạn $AM$ nên $AN = \dfrac{1}{2}AM$ hay $AM = 2AN = 2.1,5 = 3cm$
Lại có điểm $M$ là trung điểm đoạn thẳng $AB$ nên ta có $AM = \dfrac{1}{2}AB$ hay $AB = 2AM = 2.3 = 6cm$
Vậy $AB = 6cm$.
Cho đoạn thẳng $AB = 8cm$. Gọi $I$ và $K$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AI.$ Đoạn thẳng $IK$ có độ dài là?
$8cm$
$4cm$
$2cm$
$6cm$
Đáp án : C
Sử dụng kiến thức về trung điểm đoạn thẳng : “\(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$” để tính toán.

Vì điểm $I$ là trung điểm đoạn thẳng $AB$ nên $AI = \dfrac{1}{2}AB = \dfrac{1}{2}.8 = 4cm$
Vì điểm $K$ là trung điểm đoạn thẳng $AI$ nên $AK = \dfrac{1}{2}AI = \dfrac{1}{2}.4 = 2cm$
Vậy $AI = 2cm$.
Trên tia $Ox$ lấy các điểm $M,{\rm{ }}N$ sao cho $OM = 2cm;ON = 3cm.$Trên tia đối của tia $NO$ lấy điểm $P$ sao cho $NP = 1cm.$
Tính độ dài các đoạn thẳng $MN$ và $MP.$
$MN = 1cm;\,MP = 3cm$
$MN = 2cm;\,MP = 3cm$
$MN = 2cm;\,MP = 1cm$
$MN = 1cm;\,MP = 2cm$
Đáp án: D
Sử dụng công thức cộng đoạn thẳng để tính độ dài các đoạn thẳng.

Vì hai điểm $M;N$ cùng thuộc tia $Ox$ mà $OM < ON\left( {2cm < 3cm} \right)$ nên điểm $M$ nằm giữa hai điểm $O$ và $N$.
Do đó $OM + MN = ON \Rightarrow MN = ON - OM$ $ = 3 - 2 = 1cm$
Vì hai tia $NP$ và $NO$ đối nhau mà $M$ nằm giữa hai điểm $O$ và $N$ nên $N$ là điểm nằm giữa $M$ và $P$
Do đó $MN + NP = MP$ hay $MP = 1 + 1 = 2cm$.
Vậy $MN = 1cm;\,MP = 2cm$.
Hãy chọn câu đúng nhất
$N$ là trung điểm của đoạn thẳng $MP.$
$M$ là trung điểm của đoạn thẳng $OP.$
$M$ là trung điểm của đoạn thẳng $NP. $
Cả A, B đều đúng.
Đáp án: D
Ta sử dụng kiến thức sau:
Nếu \(M\) nằm giữa \(A\) và \(B\) đồng thời \(MA = MB\) thì \(M\) là trung điểm của \(AB.\)

Từ câu trước và đề bài ta có $MN = 1cm;\,MP = 2cm;\,OM = 2cm;NP = 1cm$
Suy ra $MN = NP\left( { = 1cm} \right)\,\,\,\left( 1 \right);\,MP = OM\left( { = 2cm} \right)\,\left( 2 \right)$
Lại có $M$ nằm giữa hai điểm $O$ và $N$ mà $N$ nằm giữa hai điểm $M$ và $P$ nên điểm $M$ nằm giữa hai điểm $O$ và $P$ (3)
Từ (2) và (3) ta có $M$ là trung điểm đoạn $OP.$
Theo câu trước ta có $N$ là điểm nằm giữa $M$ và $P$ nên kết hợp với $\left( 1 \right)$ suy ra $N$ là trung điểm đoạn $MP$.
Nên cả A, B đều đúng.
Cho đoạn thẳng $AB$ dài $14cm.$ Trên tia $AB$ lấy điểm $M$ sao cho $AM = 7cm.$ Chọn câu sai.
\(M\) nằm giữa \(A\) và \(B.\)
\(AM = BM = 7\,cm\)
\(BM = AB\)
\(M\) là trung điểm của \(AB.\)
Đáp án : C
Sử dụng kiến thức về điểm nằm giữa hai điểm và trung điểm của đoạn thẳng: “ Nếu \(M\) nằm giữa \(A\) và \(B\) đồng thời \(MA = MB\) thì \(M\) là trung điểm của \(AB.\)”

Vì điểm $M$ thuộc tia $AB$ mà $AM < AB\left( {7cm < 14cm} \right)$ nên điểm $M$ nằm giữa hai điểm $A$ và $B$. (1)
Do đó $AM + MB = AB$ $ \Rightarrow MB = AB - AM = 14 - 7 = 7cm$. Suy ra $AM = MB = 7cm$ (2)
Từ (1) và (2) suy ra $M$ là trung điểm của đoạn $AB$.
Vậy các đáp án A, B, D đúng và C sai vì $BM = 7cm < 14cm = AB$.
Trên tia $Ox$ có các điểm $A,{\rm{ }}B$ sao cho $OA = 2cm;OB = 5cm.$ Gọi $M$ là trung điểm của đoạn thẳng $OB.$ Tính độ dài đoạn thẳng $AM.$
$AM = 1,5cm.$
$AM = 0,5cm.$
$AM = 1cm.$
$AM = 2cm.$
Đáp án : B
+ Sử dụng tính chất trung điểm của đoạn thẳng: “\(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$” để tính đoạn $OM$.
+ Sử dụng công thức cộng đoạn thẳng để tính đoạn $AM$.

Vì $M$ là trung điểm của đoạn thẳng $OB$ nên ta có $OM = \dfrac{1}{2}OB = \dfrac{1}{2}.5 = 2,5cm$
Vì $A$ và $M$ cùng thuộc tia $Ox$ mà $OA < OM\,\left( {2cm < 2,5cm} \right)$ nên điểm $A$ nằm giữa hai điểm $O$ và $M$.
Do đó $OA + AM = OM$ $ \Rightarrow AM = OM - OA = 2,5 - 2 = 0,5cm$
Vậy $AM = 0,5cm.$
Bài 5 trong chương trình Toán 6 Chân trời sáng tạo tập trung vào khái niệm quan trọng: trung điểm của một đoạn thẳng. Hiểu rõ khái niệm này là nền tảng cho nhiều bài học hình học tiếp theo. Bài viết này sẽ cung cấp một cái nhìn tổng quan về bài học, các định nghĩa, tính chất và hướng dẫn giải các dạng bài tập thường gặp.
Trung điểm M của đoạn thẳng AB là điểm nằm giữa A và B sao cho AM = MB. Nói cách khác, M chia đoạn thẳng AB thành hai đoạn thẳng bằng nhau.
Ví dụ: Cho đoạn thẳng CD có độ dài 10cm. Gọi E là trung điểm của CD. Tính độ dài CE và DE.
Giải: Vì E là trung điểm của CD nên CE = DE = CD/2 = 10cm/2 = 5cm.
Ví dụ: Cho đoạn thẳng MN có trung điểm P. Biết MP = 7cm. Tính độ dài MN.
Giải: Vì P là trung điểm của MN nên MN = 2 * MP = 2 * 7cm = 14cm.
Ví dụ: Trên đoạn thẳng AB dài 12cm, lấy điểm M sao cho AM = 4cm. Gọi I là trung điểm của đoạn thẳng MB. Tính độ dài MI.
Giải:
Trong quá trình giải bài tập, cần chú ý:
Dưới đây là một số câu hỏi trắc nghiệm minh họa để các em luyện tập:
A. 2cm B. 4cm C. 6cm D. 8cm
A. 2.5cm B. 5cm C. 10cm D. 15cm
Bài học về trung điểm của đoạn thẳng là một khái niệm cơ bản nhưng vô cùng quan trọng trong hình học. Việc nắm vững kiến thức và luyện tập thường xuyên sẽ giúp các em giải quyết các bài toán một cách dễ dàng và hiệu quả. Giaitoan.edu.vn hy vọng bài viết này đã cung cấp cho các em những thông tin hữu ích và giúp các em học tốt môn Toán.