Bài tập trắc nghiệm Bài 6: Góc - Toán 6 Chân trời sáng tạo là công cụ hỗ trợ học sinh ôn luyện và kiểm tra kiến thức về góc, các loại góc (nhọn, vuông, tù, bẹt), cách đo góc và so sánh góc. Bài tập được thiết kế đa dạng, bám sát chương trình học, giúp học sinh hiểu rõ lý thuyết và áp dụng vào giải bài tập.
Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm phong phú, kèm đáp án chi tiết và lời giải thích dễ hiểu, giúp học sinh tự học hiệu quả tại nhà.
Chọn câu sai.
Góc là hình gồm hai tia chung gốc
Hai tia chung gốc tạo thành góc bẹt
Hai góc bằng nhau có số đo bằng nhau
Hai góc có số đo bằng nhau thì bằng nhau
Cho hình vẽ sau
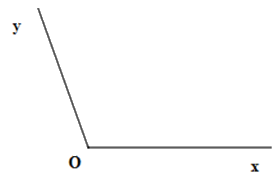
Chọn câu đúng.
\(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xyO}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {Oxy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xOy}\), đỉnh \(y\) , cạnh \(Ox\) và \(Oy\) .
Kể tên các góc có trên hình vẽ
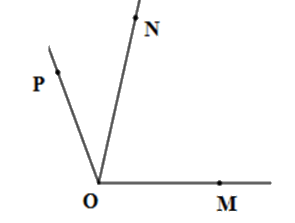
\(\widehat {MON}\)
\(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
\(\widehat {MON};\widehat {NOP}\)
\(\widehat {NOP};\,\widehat {MOP}\)
Kể tên tất cả các góc có một cạnh là \(Om\) có trên hình vẽ sau
\(\widehat {xOm};\,\widehat {mOn}\)
\(\,\widehat {mOn}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy};\widehat {xOy}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\)
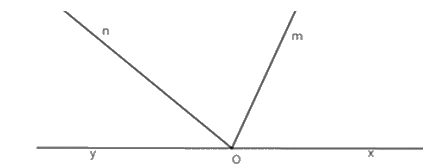
Gọi \(O\) là giao điểm của ba đường thẳng \(xy;zt;uv\). Kể tên các góc bẹt đỉnh \(O.\)
\(\widehat {xOu};\,\widehat {uOt};\,\widehat {tOx}\)
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\)
\(\widehat {xOy};\,\widehat {uOv}\)
\(\,\widehat {uOv};\,\widehat {zOt}\)
Cho \(n\left( {n \ge 2} \right)\) tia chung gốc, trong đó không có hai tia nào trùng nhau. Nếu có \(28\) góc tạo thành thì \(n\) bằng bao nhiêu?
\(8\)
\(7\)
\(6\)
\(9\)
Cho trước \(4\) tia chung gốc \(O.\) Vẽ thêm \(3\) tia gốc \(O\) không trùng với các tia cho trước. Hỏi đã tăng thêm bao nhiêu góc đỉnh \(O?\)
\(3\)
\(6\)
\(15\)
\(18\)
Giả sử có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) thì số góc tạo thành là
\(2n\left( {n - 1} \right)\)
\(\dfrac{{n\left( {n - 1} \right)}}{2}\)
\(2n\left( {2n - 1} \right)\)
\(n\left( {2n - 1} \right)\)
Cho góc \(xOy\) khác góc bẹt, tia \(Oz\) nằm giữa hai tia \(Ox;Oy\). Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\). Lấy điểm \(A \in Ox;\,B \in Oy\), đường thẳng \(AB\) cắt tia \(Oz;Ot\) theo thứ tự tại \(M;N\). Chọn câu sai.
Điểm \(N\) nằm trong góc \(xOz.\)
Điểm \(M\) nằm trong góc \(yOt.\)
Điểm \(A\) nằm trong góc \(tOz.\)
Cả A, B đều đúng.
Cho \(9\) tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là
\(16\)
\(72\)
\(36\)
\(42\)
Lời giải và đáp án
Chọn câu sai.
Góc là hình gồm hai tia chung gốc
Hai tia chung gốc tạo thành góc bẹt
Hai góc bằng nhau có số đo bằng nhau
Hai góc có số đo bằng nhau thì bằng nhau
Đáp án : B
Sử dụng kiến thức về góc và so sánh hai góc
Để so sánh hai góc ta so sánh số đo của chúng
Ta có:
+ Góc là hình gồm hai tia chung gốc nên A đúng
+ Góc bẹt là góc có hai cạnh là hai tia đối nhau nên B sai vì hai tia chung gốc chưa chắc đã đối nhau
+ Hai góc bằng nhau có số đo bằng nhau nên C đúng
+ Hai góc có số đo bằng nhau thì bằng nhau nên D đúng
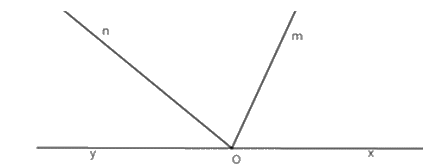
Cho hình vẽ sau
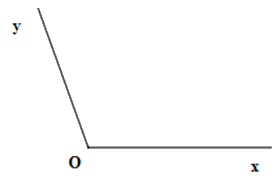
Chọn câu đúng.
\(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xyO}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {Oxy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xOy}\), đỉnh \(y\) , cạnh \(Ox\) và \(Oy\) .
Đáp án : A
Áp dụng cách đọc góc, phân biệt được đỉnh và cạnh của góc.
Góc trên hình là góc \(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
Kể tên các góc có trên hình vẽ
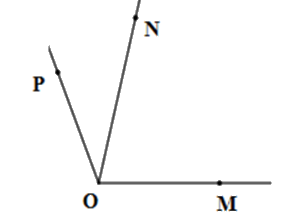
\(\widehat {MON}\)
\(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
\(\widehat {MON};\widehat {NOP}\)
\(\widehat {NOP};\,\widehat {MOP}\)
Đáp án : B
Quan sát hình vẽ, xác định các tia phân biệt chung gốc \(O\) từ đó tìm các góc tạo thành.
Các góc tạo thành là: \(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
Kể tên tất cả các góc có một cạnh là \(Om\) có trên hình vẽ sau
\(\widehat {xOm};\,\widehat {mOn}\)
\(\,\widehat {mOn}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy};\widehat {xOy}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\)
Đáp án : D
Xác định các tia chung gốc \(O\) từ đó xác định các góc có một cạnh là \(Om.\)
Các góc cần tìm là \(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\) .
Gọi \(O\) là giao điểm của ba đường thẳng \(xy;zt;uv\). Kể tên các góc bẹt đỉnh \(O.\)
\(\widehat {xOu};\,\widehat {uOt};\,\widehat {tOx}\)
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\)
\(\widehat {xOy};\,\widehat {uOv}\)
\(\,\widehat {uOv};\,\widehat {zOt}\)
Đáp án : B
Xác định các tia phân biệt đối nhau từ đó kể tên các góc bẹt.
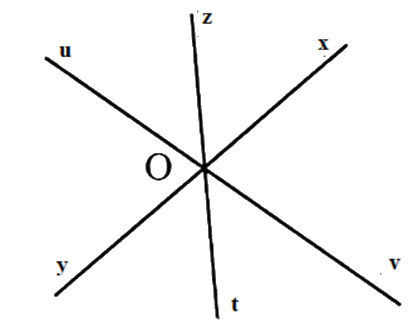
Các tia \(Ox\) và \(Oy;\) \(Oz\) và \(Ot;Ou\) và \(Ov\) là hai tia đối nhau nên các góc bẹt có đỉnh \(O\) tạo thành là
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\) .
Cho \(n\left( {n \ge 2} \right)\) tia chung gốc, trong đó không có hai tia nào trùng nhau. Nếu có \(28\) góc tạo thành thì \(n\) bằng bao nhiêu?
\(8\)
\(7\)
\(6\)
\(9\)
Đáp án : A
Sử dụng:
Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Từ đó tìm ra \(n.\)
Từ đề bài ta có \(\dfrac{{n\left( {n - 1} \right)}}{2} = 28\) nên \(n\left( {n - 1} \right) = 56\) mà \(56 = 8.7\), lại có $(n-1)$ và $n$ là hai số tự nhiên liên tiếp nên \(n = 8.\)
Vậy \(n = 8.\)
Cho trước \(4\) tia chung gốc \(O.\) Vẽ thêm \(3\) tia gốc \(O\) không trùng với các tia cho trước. Hỏi đã tăng thêm bao nhiêu góc đỉnh \(O?\)
\(3\)
\(6\)
\(15\)
\(18\)
Đáp án : C
Ta sử dụng công thức: Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
+ Tính số góc ban đầu
+ Tính số góc sau khi thêm
+ Tính số góc tăng thêm
Số góc tạo thành khi có \(4\) tia chung gốc là \(\dfrac{{4.\left( {4 - 1} \right)}}{2} = 6\) góc
Số góc tạo thành khi có thêm ba tia chung gốc \(O\) nữa là \(\dfrac{{7.\left( {7 - 1} \right)}}{2} = 21\) góc
Số góc tăng thêm là \(21 - 6 = 15\) góc
Giả sử có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) thì số góc tạo thành là
\(2n\left( {n - 1} \right)\)
\(\dfrac{{n\left( {n - 1} \right)}}{2}\)
\(2n\left( {2n - 1} \right)\)
\(n\left( {2n - 1} \right)\)
Đáp án : D
+ Xác định số lượng các tia phân biệt chung gốc \(O.\)
+ Tính góc theo công thức: Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Vì có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) nên số các tia chung gốc tạo thành là \(2n\) tia.
Số góc tạo thành là \(\dfrac{{2n\left( {2n - 1} \right)}}{2} = n\left( {2n - 1} \right)\) góc.
Cho góc \(xOy\) khác góc bẹt, tia \(Oz\) nằm giữa hai tia \(Ox;Oy\). Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\). Lấy điểm \(A \in Ox;\,B \in Oy\), đường thẳng \(AB\) cắt tia \(Oz;Ot\) theo thứ tự tại \(M;N\). Chọn câu sai.
Điểm \(N\) nằm trong góc \(xOz.\)
Điểm \(M\) nằm trong góc \(yOt.\)
Điểm \(A\) nằm trong góc \(tOz.\)
Cả A, B đều đúng.
Đáp án : C
Sử dụng: Khi hai tia \(Ox;Oy\) không đối nhau, điểm \(M\) là điểm nằm bên trong góc \(xOy\) nếu tia \(OM\) nằm giữa hai tia \(Ox;Oy\).
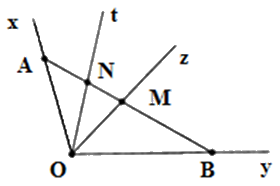
Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) mà điểm \(N\) thuộc tia \(Ot\) nên điểm \(N\) nằm trong góc \(xOz\). Do đó A đúng.
Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) nên điểm \(N\) và điểm \(A\) nằm cùng phía đối với điểm \(M.\)
Tia \(Oz\) nằm giữa hai tia \(Ox;Oy\) nên điểm \(A;B\) nằm khác phía đối với điểm \(M.\) Suy ra điểm \(N\) và điểm \(B\) nằm khác phía đối với điểm \(M\), do đó điểm \(M\) nằm trong góc \(yOt.\) Do đó B đúng, D đúng.
Vì \(A \in Ox\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) nên điểm \(A\) không nằm trong góc \(tOz.\) Do đó C sai.
Cho \(9\) tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là
\(16\)
\(72\)
\(36\)
\(42\)
Đáp án : C
Ta sử dụng kiến thức:
Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Số góc tạo thành là \(\dfrac{{9.\left( {9 - 1} \right)}}{2} = 36\) góc.
Chọn câu sai.
Góc là hình gồm hai tia chung gốc
Hai tia chung gốc tạo thành góc bẹt
Hai góc bằng nhau có số đo bằng nhau
Hai góc có số đo bằng nhau thì bằng nhau
Cho hình vẽ sau

Chọn câu đúng.
\(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xyO}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {Oxy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xOy}\), đỉnh \(y\) , cạnh \(Ox\) và \(Oy\) .
Kể tên các góc có trên hình vẽ

\(\widehat {MON}\)
\(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
\(\widehat {MON};\widehat {NOP}\)
\(\widehat {NOP};\,\widehat {MOP}\)
Kể tên tất cả các góc có một cạnh là \(Om\) có trên hình vẽ sau

\(\widehat {xOm};\,\widehat {mOn}\)
\(\,\widehat {mOn}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy};\widehat {xOy}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\)
Gọi \(O\) là giao điểm của ba đường thẳng \(xy;zt;uv\). Kể tên các góc bẹt đỉnh \(O.\)
\(\widehat {xOu};\,\widehat {uOt};\,\widehat {tOx}\)
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\)
\(\widehat {xOy};\,\widehat {uOv}\)
\(\,\widehat {uOv};\,\widehat {zOt}\)
Cho \(n\left( {n \ge 2} \right)\) tia chung gốc, trong đó không có hai tia nào trùng nhau. Nếu có \(28\) góc tạo thành thì \(n\) bằng bao nhiêu?
\(8\)
\(7\)
\(6\)
\(9\)
Cho trước \(4\) tia chung gốc \(O.\) Vẽ thêm \(3\) tia gốc \(O\) không trùng với các tia cho trước. Hỏi đã tăng thêm bao nhiêu góc đỉnh \(O?\)
\(3\)
\(6\)
\(15\)
\(18\)
Giả sử có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) thì số góc tạo thành là
\(2n\left( {n - 1} \right)\)
\(\dfrac{{n\left( {n - 1} \right)}}{2}\)
\(2n\left( {2n - 1} \right)\)
\(n\left( {2n - 1} \right)\)
Cho góc \(xOy\) khác góc bẹt, tia \(Oz\) nằm giữa hai tia \(Ox;Oy\). Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\). Lấy điểm \(A \in Ox;\,B \in Oy\), đường thẳng \(AB\) cắt tia \(Oz;Ot\) theo thứ tự tại \(M;N\). Chọn câu sai.
Điểm \(N\) nằm trong góc \(xOz.\)
Điểm \(M\) nằm trong góc \(yOt.\)
Điểm \(A\) nằm trong góc \(tOz.\)
Cả A, B đều đúng.
Cho \(9\) tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là
\(16\)
\(72\)
\(36\)
\(42\)
Chọn câu sai.
Góc là hình gồm hai tia chung gốc
Hai tia chung gốc tạo thành góc bẹt
Hai góc bằng nhau có số đo bằng nhau
Hai góc có số đo bằng nhau thì bằng nhau
Đáp án : B
Sử dụng kiến thức về góc và so sánh hai góc
Để so sánh hai góc ta so sánh số đo của chúng
Ta có:
+ Góc là hình gồm hai tia chung gốc nên A đúng
+ Góc bẹt là góc có hai cạnh là hai tia đối nhau nên B sai vì hai tia chung gốc chưa chắc đã đối nhau
+ Hai góc bằng nhau có số đo bằng nhau nên C đúng
+ Hai góc có số đo bằng nhau thì bằng nhau nên D đúng
Cho hình vẽ sau

Chọn câu đúng.
\(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xyO}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {Oxy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
\(\widehat {xOy}\), đỉnh \(y\) , cạnh \(Ox\) và \(Oy\) .
Đáp án : A
Áp dụng cách đọc góc, phân biệt được đỉnh và cạnh của góc.
Góc trên hình là góc \(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
Kể tên các góc có trên hình vẽ

\(\widehat {MON}\)
\(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
\(\widehat {MON};\widehat {NOP}\)
\(\widehat {NOP};\,\widehat {MOP}\)
Đáp án : B
Quan sát hình vẽ, xác định các tia phân biệt chung gốc \(O\) từ đó tìm các góc tạo thành.
Các góc tạo thành là: \(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
Kể tên tất cả các góc có một cạnh là \(Om\) có trên hình vẽ sau

\(\widehat {xOm};\,\widehat {mOn}\)
\(\,\widehat {mOn}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy};\widehat {xOy}\)
\(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\)
Đáp án : D
Xác định các tia chung gốc \(O\) từ đó xác định các góc có một cạnh là \(Om.\)
Các góc cần tìm là \(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\) .
Gọi \(O\) là giao điểm của ba đường thẳng \(xy;zt;uv\). Kể tên các góc bẹt đỉnh \(O.\)
\(\widehat {xOu};\,\widehat {uOt};\,\widehat {tOx}\)
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\)
\(\widehat {xOy};\,\widehat {uOv}\)
\(\,\widehat {uOv};\,\widehat {zOt}\)
Đáp án : B
Xác định các tia phân biệt đối nhau từ đó kể tên các góc bẹt.

Các tia \(Ox\) và \(Oy;\) \(Oz\) và \(Ot;Ou\) và \(Ov\) là hai tia đối nhau nên các góc bẹt có đỉnh \(O\) tạo thành là
\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\) .
Cho \(n\left( {n \ge 2} \right)\) tia chung gốc, trong đó không có hai tia nào trùng nhau. Nếu có \(28\) góc tạo thành thì \(n\) bằng bao nhiêu?
\(8\)
\(7\)
\(6\)
\(9\)
Đáp án : A
Sử dụng:
Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Từ đó tìm ra \(n.\)
Từ đề bài ta có \(\dfrac{{n\left( {n - 1} \right)}}{2} = 28\) nên \(n\left( {n - 1} \right) = 56\) mà \(56 = 8.7\), lại có $(n-1)$ và $n$ là hai số tự nhiên liên tiếp nên \(n = 8.\)
Vậy \(n = 8.\)
Cho trước \(4\) tia chung gốc \(O.\) Vẽ thêm \(3\) tia gốc \(O\) không trùng với các tia cho trước. Hỏi đã tăng thêm bao nhiêu góc đỉnh \(O?\)
\(3\)
\(6\)
\(15\)
\(18\)
Đáp án : C
Ta sử dụng công thức: Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
+ Tính số góc ban đầu
+ Tính số góc sau khi thêm
+ Tính số góc tăng thêm
Số góc tạo thành khi có \(4\) tia chung gốc là \(\dfrac{{4.\left( {4 - 1} \right)}}{2} = 6\) góc
Số góc tạo thành khi có thêm ba tia chung gốc \(O\) nữa là \(\dfrac{{7.\left( {7 - 1} \right)}}{2} = 21\) góc
Số góc tăng thêm là \(21 - 6 = 15\) góc
Giả sử có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) thì số góc tạo thành là
\(2n\left( {n - 1} \right)\)
\(\dfrac{{n\left( {n - 1} \right)}}{2}\)
\(2n\left( {2n - 1} \right)\)
\(n\left( {2n - 1} \right)\)
Đáp án : D
+ Xác định số lượng các tia phân biệt chung gốc \(O.\)
+ Tính góc theo công thức: Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Vì có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) nên số các tia chung gốc tạo thành là \(2n\) tia.
Số góc tạo thành là \(\dfrac{{2n\left( {2n - 1} \right)}}{2} = n\left( {2n - 1} \right)\) góc.
Cho góc \(xOy\) khác góc bẹt, tia \(Oz\) nằm giữa hai tia \(Ox;Oy\). Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\). Lấy điểm \(A \in Ox;\,B \in Oy\), đường thẳng \(AB\) cắt tia \(Oz;Ot\) theo thứ tự tại \(M;N\). Chọn câu sai.
Điểm \(N\) nằm trong góc \(xOz.\)
Điểm \(M\) nằm trong góc \(yOt.\)
Điểm \(A\) nằm trong góc \(tOz.\)
Cả A, B đều đúng.
Đáp án : C
Sử dụng: Khi hai tia \(Ox;Oy\) không đối nhau, điểm \(M\) là điểm nằm bên trong góc \(xOy\) nếu tia \(OM\) nằm giữa hai tia \(Ox;Oy\).

Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) mà điểm \(N\) thuộc tia \(Ot\) nên điểm \(N\) nằm trong góc \(xOz\). Do đó A đúng.
Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) nên điểm \(N\) và điểm \(A\) nằm cùng phía đối với điểm \(M.\)
Tia \(Oz\) nằm giữa hai tia \(Ox;Oy\) nên điểm \(A;B\) nằm khác phía đối với điểm \(M.\) Suy ra điểm \(N\) và điểm \(B\) nằm khác phía đối với điểm \(M\), do đó điểm \(M\) nằm trong góc \(yOt.\) Do đó B đúng, D đúng.
Vì \(A \in Ox\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) nên điểm \(A\) không nằm trong góc \(tOz.\) Do đó C sai.
Cho \(9\) tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là
\(16\)
\(72\)
\(36\)
\(42\)
Đáp án : C
Ta sử dụng kiến thức:
Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\)
Số góc tạo thành là \(\dfrac{{9.\left( {9 - 1} \right)}}{2} = 36\) góc.
Bài 6 trong chương trình Toán 6 Chân trời sáng tạo tập trung vào khái niệm cơ bản về góc, các loại góc và cách đo góc. Việc nắm vững kiến thức này là nền tảng quan trọng cho các bài học tiếp theo về hình học.
Góc là hình tạo bởi hai tia chung gốc. Gốc của hai tia đó là đỉnh của góc, hai tia là hai cạnh của góc. Để xác định một góc, ta thường dùng ký hiệu ∠ (góc). Ví dụ: ∠ABC là góc có đỉnh B và hai cạnh là BA và BC.
Có bốn loại góc chính:
Góc được đo bằng độ (°). Để đo góc, ta sử dụng thước đo góc. Cách sử dụng thước đo góc:
Để so sánh hai góc, ta so sánh số đo của chúng. Góc nào có số đo lớn hơn thì góc đó lớn hơn.
Dưới đây là một số bài tập trắc nghiệm minh họa để giúp bạn hiểu rõ hơn về bài học:
Câu 1: Góc nào sau đây là góc nhọn?
Câu 2: Góc vuông có số đo bằng bao nhiêu?
Để củng cố kiến thức về bài 6, bạn nên thực hành giải nhiều bài tập trắc nghiệm khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập đa dạng, được phân loại theo mức độ khó, giúp bạn luyện tập hiệu quả.
Ngoài các kiến thức cơ bản về góc, bạn có thể tìm hiểu thêm về:
Kiến thức về góc có ứng dụng rộng rãi trong thực tế, chẳng hạn như trong kiến trúc, xây dựng, hàng hải, và nhiều lĩnh vực khác.
Đối với các bài tập nâng cao, bạn cần vận dụng linh hoạt các kiến thức đã học và kết hợp với các kỹ năng tư duy logic để tìm ra lời giải chính xác.
Bài 6: Góc - Toán 6 Chân trời sáng tạo là một bài học quan trọng, giúp học sinh làm quen với các khái niệm cơ bản về hình học. Việc luyện tập thường xuyên và nắm vững kiến thức là chìa khóa để thành công trong môn Toán.