Bài viết này cung cấp bộ câu hỏi trắc nghiệm giúp học sinh lớp 6 ôn luyện và kiểm tra kiến thức về số nguyên âm và tập hợp các số nguyên, thuộc chương trình Toán 6 Chân trời sáng tạo. Các câu hỏi được thiết kế đa dạng, bám sát nội dung sách giáo khoa, giúp học sinh rèn luyện kỹ năng giải bài tập một cách hiệu quả.
Với đáp án chi tiết đi kèm, các em có thể tự đánh giá năng lực của mình và tìm ra những điểm cần cải thiện.
Tập hợp các số nguyên kí hiệu là
$N$
${N^*}$
$Z$
${Z^*}$
Số đối của số \( - 3\) là
$3$
$ - 3$
$2$
$4$

Cho số nguyên \(a\), biết điểm \(a\) cách điểm \(0\) là \(6\) đơn vị. Có bao nhiêu số như vậy?

Cho trục số:
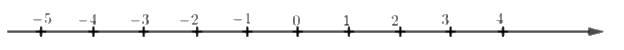
Điểm \( - 4\) cách điểm \(3\) bao nhiêu đơn vị?
Tập hợp nào dưới đây gồm các số nguyên âm
\(\left\{ { - 3;\,\, - 2;\,\,1} \right\}\)
\(\left\{ { - 9;\, - 2;\, - 1} \right\}\)
Cách viết nào sau đây là đúng:
Một tàu ngầm đang ở vị trí dưới mực nước biển 120 m. Số nguyên âm biểu thị độ cao của tàu so với mực nước biển là:
Hãy đọc số nguyên âm chỉ nhiệt độ dưới \({0^o}C\) sau đây: \( - {4^o}C\).
Bốn độ C
Âm bốn độ C
Lời giải và đáp án
Tập hợp các số nguyên kí hiệu là
$N$
${N^*}$
$Z$
${Z^*}$
Đáp án : C
Tập hợp các số nguyên kí hiệu là $Z.$
Số đối của số \( - 3\) là
$3$
$ - 3$
$2$
$4$
Đáp án : A
- Sử dụng: Số đối của \(a\) là \( - a.\)
Ta có số đối của số \( - 3\) là \(3.\)

Đáp án : B
Cho số nguyên \(a\), biết điểm \(a\) cách điểm \(0\) là \(6\) đơn vị. Có bao nhiêu số như vậy?
Đáp án : B

Đáp án : B
Hai vạch liên tiếp của nhiệt kế cách nhau 1 đơn vị.
Coi nhiệt kế như trục số thẳng đứng, chiều dương từ dưới lên trên.
Cho trục số:
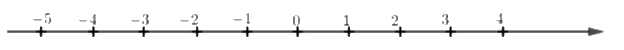
Điểm \( - 4\) cách điểm \(3\) bao nhiêu đơn vị?
Đáp án : C
Đếm xem điểm \( - 4\) cách điểm \(3\) bao nhiêu khoảng, mỗi khoảng là 1 đơn vị.
Ta thấy điểm \( - 4\) cách điểm \(3\) bảy đơn vị.
Tập hợp nào dưới đây gồm các số nguyên âm
\(\left\{ { - 3;\,\, - 2;\,\,1} \right\}\)
\(\left\{ { - 9;\, - 2;\, - 1} \right\}\)
Đáp án : B
Các số \( - 1,\,\, - 2,\,\, - 3,\,...\) gọi là các số nguyên âm.
Đáp án A: Số \(1\) không là số nguyên âm
Đáp án B: Tất cả các số đều là số nguyên âm
Đáp án C: Số \(1;\,\,4\) không là số nguyên âm
Đáp án D: Cả ba số đều không là số nguyên âm.
Cách viết nào sau đây là đúng:
Đáp án : C
\(\begin{array}{l}\mathbb{N} = \left\{ {0;\,\,1;\,\,2;\,\,3;\,...} \right\}\\\mathbb{Z} = \left\{ {...;\, - 2;\, - 1;\,0;\,\,1;\,\,2;...} \right\}\end{array}\)
\( - 2\) không là số tự nhiên => Asai.
\(1,5\) và \(1\dfrac{1}{2}\) không là số nguyên => B, Dsai.
\( - 31\) là số nguyên => Cđúng.
Một tàu ngầm đang ở vị trí dưới mực nước biển 120 m. Số nguyên âm biểu thị độ cao của tàu so với mực nước biển là:
Đáp án : B
Số nguyên âm biểu thị vị trí dưới mực nước biển \(a\,\,\left( m \right)\) là: \( - a\,\,\left( m \right)\).
Số nguyên âm biểu thị độ cao của tàu so với mực nước biển là: \( - 120\,\,m\).
Hãy đọc số nguyên âm chỉ nhiệt độ dưới \({0^o}C\) sau đây: \( - {4^o}C\).
Bốn độ C
Âm bốn độ C
Đáp án : D
Dấu “\( - \)” đọc là “âm”, đọc “âm” rồi đọc số tự nhiên.
\(^\circ C\): độ C
\( - 4^\circ C\): đọc là “âm bốn độ C” hoặc “trừ bốn độ C”.
Đáp án : C
Phương án A sai. Ví dụ \( - 2 > - 4\) nhưng \( - 2\) là số nguyên âm.
Phương án B sai. Ví dụ \(1 < 3\) nhưng 1 là số dương.
Phương án D sai vì các số nguyên nhỏ hơn \(0\) là các số nguyên âm.
Phương án C đúng.
Tập hợp các số nguyên kí hiệu là
$N$
${N^*}$
$Z$
${Z^*}$
Số đối của số \( - 3\) là
$3$
$ - 3$
$2$
$4$

Cho số nguyên \(a\), biết điểm \(a\) cách điểm \(0\) là \(6\) đơn vị. Có bao nhiêu số như vậy?

Cho trục số:
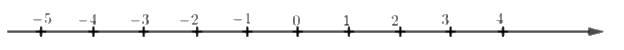
Điểm \( - 4\) cách điểm \(3\) bao nhiêu đơn vị?
Tập hợp nào dưới đây gồm các số nguyên âm
\(\left\{ { - 3;\,\, - 2;\,\,1} \right\}\)
\(\left\{ { - 9;\, - 2;\, - 1} \right\}\)
Cách viết nào sau đây là đúng:
Một tàu ngầm đang ở vị trí dưới mực nước biển 120 m. Số nguyên âm biểu thị độ cao của tàu so với mực nước biển là:
Hãy đọc số nguyên âm chỉ nhiệt độ dưới \({0^o}C\) sau đây: \( - {4^o}C\).
Bốn độ C
Âm bốn độ C
Tập hợp các số nguyên kí hiệu là
$N$
${N^*}$
$Z$
${Z^*}$
Đáp án : C
Tập hợp các số nguyên kí hiệu là $Z.$
Số đối của số \( - 3\) là
$3$
$ - 3$
$2$
$4$
Đáp án : A
- Sử dụng: Số đối của \(a\) là \( - a.\)
Ta có số đối của số \( - 3\) là \(3.\)

Đáp án : B
Cho số nguyên \(a\), biết điểm \(a\) cách điểm \(0\) là \(6\) đơn vị. Có bao nhiêu số như vậy?
Đáp án : B

Đáp án : B
Hai vạch liên tiếp của nhiệt kế cách nhau 1 đơn vị.
Coi nhiệt kế như trục số thẳng đứng, chiều dương từ dưới lên trên.
Cho trục số:
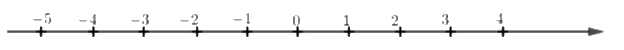
Điểm \( - 4\) cách điểm \(3\) bao nhiêu đơn vị?
Đáp án : C
Đếm xem điểm \( - 4\) cách điểm \(3\) bao nhiêu khoảng, mỗi khoảng là 1 đơn vị.
Ta thấy điểm \( - 4\) cách điểm \(3\) bảy đơn vị.
Tập hợp nào dưới đây gồm các số nguyên âm
\(\left\{ { - 3;\,\, - 2;\,\,1} \right\}\)
\(\left\{ { - 9;\, - 2;\, - 1} \right\}\)
Đáp án : B
Các số \( - 1,\,\, - 2,\,\, - 3,\,...\) gọi là các số nguyên âm.
Đáp án A: Số \(1\) không là số nguyên âm
Đáp án B: Tất cả các số đều là số nguyên âm
Đáp án C: Số \(1;\,\,4\) không là số nguyên âm
Đáp án D: Cả ba số đều không là số nguyên âm.
Cách viết nào sau đây là đúng:
Đáp án : C
\(\begin{array}{l}\mathbb{N} = \left\{ {0;\,\,1;\,\,2;\,\,3;\,...} \right\}\\\mathbb{Z} = \left\{ {...;\, - 2;\, - 1;\,0;\,\,1;\,\,2;...} \right\}\end{array}\)
\( - 2\) không là số tự nhiên => Asai.
\(1,5\) và \(1\dfrac{1}{2}\) không là số nguyên => B, Dsai.
\( - 31\) là số nguyên => Cđúng.
Một tàu ngầm đang ở vị trí dưới mực nước biển 120 m. Số nguyên âm biểu thị độ cao của tàu so với mực nước biển là:
Đáp án : B
Số nguyên âm biểu thị vị trí dưới mực nước biển \(a\,\,\left( m \right)\) là: \( - a\,\,\left( m \right)\).
Số nguyên âm biểu thị độ cao của tàu so với mực nước biển là: \( - 120\,\,m\).
Hãy đọc số nguyên âm chỉ nhiệt độ dưới \({0^o}C\) sau đây: \( - {4^o}C\).
Bốn độ C
Âm bốn độ C
Đáp án : D
Dấu “\( - \)” đọc là “âm”, đọc “âm” rồi đọc số tự nhiên.
\(^\circ C\): độ C
\( - 4^\circ C\): đọc là “âm bốn độ C” hoặc “trừ bốn độ C”.
Đáp án : C
Phương án A sai. Ví dụ \( - 2 > - 4\) nhưng \( - 2\) là số nguyên âm.
Phương án B sai. Ví dụ \(1 < 3\) nhưng 1 là số dương.
Phương án D sai vì các số nguyên nhỏ hơn \(0\) là các số nguyên âm.
Phương án C đúng.
Bài 1 trong chương trình Toán 6 Chân trời sáng tạo giới thiệu về số nguyên âm và tập hợp các số nguyên. Đây là nền tảng quan trọng để học sinh hiểu rõ hơn về số, thứ tự trên trục số và các phép toán trên số nguyên. Việc nắm vững kiến thức này sẽ giúp các em giải quyết các bài toán phức tạp hơn trong các chương tiếp theo.
Số nguyên âm là các số thực nhỏ hơn 0. Chúng được biểu diễn bằng dấu trừ (-) phía trước số. Ví dụ: -1, -2, -3, ... Số nguyên âm dùng để biểu diễn các đại lượng có ý nghĩa ngược lại với một đại lượng cho trước, ví dụ như nhiệt độ dưới 0 độ C, độ sâu dưới mực nước biển, hay nợ tiền.
Tập hợp các số nguyên bao gồm các số nguyên dương (1, 2, 3, ...), số 0 và các số nguyên âm (-1, -2, -3, ...). Tập hợp các số nguyên được ký hiệu là ℤ. Tập hợp các số nguyên được biểu diễn trên trục số, với số 0 là điểm gốc, các số nguyên dương nằm bên phải 0 và các số nguyên âm nằm bên trái 0.
Để so sánh hai số nguyên, ta thực hiện theo các quy tắc sau:
Dưới đây là một số câu hỏi trắc nghiệm minh họa để giúp các em làm quen với dạng bài tập này:
Đáp án: C
Đáp án: -5, -1, 0, 2, 3
Đáp án: B
Để nắm vững kiến thức về số nguyên âm và tập hợp các số nguyên, các em nên luyện tập thêm nhiều bài tập khác nhau. Các em có thể tìm thấy các bài tập này trong sách giáo khoa, sách bài tập, hoặc trên các trang web học toán online như giaitoan.edu.vn.
Số nguyên âm được ứng dụng rộng rãi trong thực tế, ví dụ như:
Hi vọng với bộ câu hỏi trắc nghiệm và các kiến thức được trình bày trong bài viết này, các em học sinh lớp 6 sẽ có thêm công cụ để ôn luyện và nắm vững kiến thức về số nguyên âm và tập hợp các số nguyên. Chúc các em học tốt!