Chào mừng các em học sinh lớp 6 đến với bài tập trắc nghiệm về các dạng toán liên quan đến phép nhân và phép chia hết hai số nguyên. Bài tập này được thiết kế theo chương trình Toán 6 Chân trời sáng tạo, giúp các em củng cố kiến thức và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm đa dạng, phong phú, bao gồm nhiều mức độ khó khác nhau, đáp ứng nhu cầu học tập của mọi đối tượng học sinh.
Chọn câu sai.
\(\left( { - 19} \right).\left( { - 7} \right) > 0\)
\(3.\left( { - 121} \right) < 0\)
\(45.\left( { - 11} \right) < - 500\)
\(46.\left( { - 11} \right) < - 500\)
Có bao nhiêu số nguyên \(x\) thỏa mãn \(\left( {x - 7} \right)\left( {x + 5} \right) < 0\)?
\(4\)
\(11\)
\(5\)
Không tồn tại \(x\)
Tập hợp các ước của $ - 8$ là:
\(A = \left\{ {1; - 1;2; - 2;4; - 4;8; - 8} \right\}\)
\(A = \left\{ {0; \pm 1; \pm 2 \pm 4 \pm 8} \right\}\)
\(A = \left\{ {1;2;4;8} \right\}\)
\(A = \left\{ {0;1;2;4;8} \right\}\)
Có bao nhiêu ước của \( - 24.\)
$9$
$17$
$8$
$16$
Giá trị lớn nhất của $a$ thỏa mãn $a + 4$ là ước của $9$ là:
$a = 5$
$a = 13$
$a = - 13$
$a = 9$
Cho \(x \in \mathbb{Z}\) và \(\left( { - 154 + x} \right) \vdots \, 3\) thì:
$x$ chia $3$ dư $1$
\(x \, \vdots \, 3\)
$x$ chia $3$ dư $2$
không kết luận được tính chia hết cho $3$ của \(x\)
Tìm $n \in Z,$ biết: $\left( {n{\rm{ }} + 5} \right) \vdots \left( {n{\rm{ }} + 1} \right)$
\(n \in \left\{ { \pm 1; \pm 2 \pm 4} \right\}\)
\(n \in \left\{ { - 5; - 3; - 2;0;1;3} \right\}\)
\(n \in \left\{ {0;1;3} \right\}\)
\(n \in \left\{ { \pm 1; \pm 5} \right\}\)
Có bao nhiêu số nguyên $a < 5$ biết: $10$ là bội của $\left( {2a + 5} \right)$
\(4\)
\(5\)
\(8\)
\(6\)
Tìm $x,$ biết: $x \, \vdots \, 6$ và $24 \, \vdots \, x$
\(x \in \left\{ { \pm 6; \pm 24} \right\}\)
\(x \in \left\{ { \pm 6; \pm 12; \pm 24} \right\}\)
\(x \in \left\{ { \pm 6; \pm 12} \right\}\)
\(\left\{ { \pm 6; \pm 12; \pm 8; \pm 24} \right\}\)
Cho \(a\) và \(b\) là hai số nguyên khác \(0.\) Biết \(a \, \vdots \, b\) và \(b \, \vdots \, a.\) Khi đó
\(a = b\)
\(a = - b\)
\(a = 2b\)
Cả A, B đều đúng
Gọi \(A\) là tập hợp các giá trị $n \in Z$ để \(\left( {{n^2} - 7} \right)\) là bội của \(\left( {n + 3} \right)\). Tổng các phần tử của \(A\) bằng:
\( - 12\)
\( - 10\)
\(0\)
\( - 8\)
Cho \(x;\,y \in \mathbb{Z}\). Nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) chia hết cho
\(6\)
\(46\)
\(16\)
\(5\)
Có bao nhiêu số nguyên \(n\) thỏa mãn \(\left( {n - 1} \right)\) là bội của \(\left( {n + 5} \right)\) và \(\left( {n + 5} \right)\) là bội của \(\left( {n - 1} \right)?\)
\(0\)
\(2\)
\(1\)
\(3\)
Trong các phát biểu sau đây, phát biểu nào đúng?
Lời giải và đáp án
Chọn câu sai.
\(\left( { - 19} \right).\left( { - 7} \right) > 0\)
\(3.\left( { - 121} \right) < 0\)
\(45.\left( { - 11} \right) < - 500\)
\(46.\left( { - 11} \right) < - 500\)
Đáp án : C
- Tính và kiểm tra các đáp án, sử dụng quy tắc nhân hai số nguyên cùng dấu, khác dấu.
Đáp án A: \(\left( { - 19} \right).\left( { - 7} \right) > 0\) đúng vì tích hai số nguyên cùng dấu là một số nguyên dương.
Đáp án B: \(3.\left( { - 121} \right) < 0\) đúng vì tích hai số nguyên khác dấu là một số nguyên âm.
Đáp án C: \(45.\left( { - 11} \right) = - 495 > - 500\) nên C sai.
Đáp án D: \(46.\left( { - 11} \right) = - 506 < - 500\) nên D đúng.
Có bao nhiêu số nguyên \(x\) thỏa mãn \(\left( {x - 7} \right)\left( {x + 5} \right) < 0\)?
\(4\)
\(11\)
\(5\)
Không tồn tại \(x\)
Đáp án : B
Sử dụng kiến thức \(A.B < 0\) thì \(A\) và \(B\) trái dấu.
\(\left( {x - 7} \right)\left( {x + 5} \right) < 0\) nên \(x - 7\) và \(x + 5\) khác dấu.
Mà \(x + 5 > x - 7\) nên \(x + 5 > 0\) và \(x - 7 < 0\)
Suy ra \(x > - 5\) và \(x < 7\)
Do đó \(x \in \left\{ { - 4, - 3, - 2, - 1,0,1,2,3,4,5,6} \right\}\)
Vậy có \(11\) giá trị nguyên của \(x\) thỏa mãn bài toán.
Tập hợp các ước của $ - 8$ là:
\(A = \left\{ {1; - 1;2; - 2;4; - 4;8; - 8} \right\}\)
\(A = \left\{ {0; \pm 1; \pm 2 \pm 4 \pm 8} \right\}\)
\(A = \left\{ {1;2;4;8} \right\}\)
\(A = \left\{ {0;1;2;4;8} \right\}\)
Đáp án : A
Sử dụng khái niệm bội và ước của một số nguyên:
Nếu $a,b,x \in Z$ và $a = b.x$ thì $a \vdots b$ và $a$ là một bội của $b;b$ là một ước của $a$
Ta có: \( - 8 = - 1.8 = 1.\left( { - 8} \right) = - 2.4 = 2.\left( { - 4} \right)\)
Tập hợp các ước của \( - 8\) là: \(A = \left\{ {1; - 1;2; - 2;4; - 4;8; - 8} \right\}\)
Có bao nhiêu ước của \( - 24.\)
$9$
$17$
$8$
$16$
Đáp án : D
Để tìm tất cả các ước của một số nguyên âm ta chỉ cần tìm tất cả các ước của số đối của số nguyên âm đó. Trước tiên ta tìm ước tự nhiên rồi thêm các ước đối của chúng.
Có \(8\) ước tự nhiên của \(24\) là: \(1;2;3;4;6;8;12;24\)
Có \(8\) ước nguyên âm của \(24\) là: \(-1;-2;-3;-4;-6;-8;-12;-24\)
Vậy có \(8.2 = 16\) ước của \( 24\) nên cũng có $16$ ước của $-24.$
Giá trị lớn nhất của $a$ thỏa mãn $a + 4$ là ước của $9$ là:
$a = 5$
$a = 13$
$a = - 13$
$a = 9$
Đáp án : A
+ Bước 1: Tìm ước của \(9\) + Bước 2: Tìm $a$ và kết luận giá trị lớn nhất của \(a\)
$a + 4$ là ước của $9$ nên $\left( {a + 4} \right) \in Ư\left( 9 \right) = \left\{ { \pm 1; \pm 3; \pm 9} \right\}\;$ Ta có bảng giá trị như sau:

Vậy giá trị lớn nhất của \(a\) là \(a = 5\)
Cho \(x \in \mathbb{Z}\) và \(\left( { - 154 + x} \right) \vdots \, 3\) thì:
$x$ chia $3$ dư $1$
\(x \, \vdots \, 3\)
$x$ chia $3$ dư $2$
không kết luận được tính chia hết cho $3$ của \(x\)
Đáp án : A
Sử dụng tính chất chia hết trong tập hợp các số nguyên $a \, \vdots \, m;b \, \vdots \, m \Rightarrow (a + b) \, \vdots \, m$
Ta có:
\(\left( { - 154 + x} \right) \, \vdots \, 3\)
\(\left( { - 153 - 1 + x} \right) \, \vdots \, 3\)
Suy ra \(\left( {x - 1} \right) \, \vdots \, 3\) (do \( - 153 \, \vdots \, 3\))
Do đó \(x - 1 = 3k \Rightarrow x = 3k + 1\)
Vậy \(x\) chia cho \(3\) dư \(1.\)
Tìm $n \in Z,$ biết: $\left( {n{\rm{ }} + 5} \right) \vdots \left( {n{\rm{ }} + 1} \right)$
\(n \in \left\{ { \pm 1; \pm 2 \pm 4} \right\}\)
\(n \in \left\{ { - 5; - 3; - 2;0;1;3} \right\}\)
\(n \in \left\{ {0;1;3} \right\}\)
\(n \in \left\{ { \pm 1; \pm 5} \right\}\)
Đáp án : B
Bước 1: Phân tích $n + 5$ về dạng $a.\left( {n + 1} \right) + b{\rm{ }}\left( {a,b\; \in \;Z,a \ne 0} \right)$ Bước 2: Tìm $n$
$\left( {n{\rm{ }} + 5} \right) \vdots \left( {n{\rm{ }} + 1} \right)$$ \Rightarrow \left( {n + 1} \right) + 4 \, \vdots \, \left( {n{\rm{ }} + 1} \right)$
Vì \(n + 1 \, \vdots \, n + 1\) và \(n \in Z\) nên để \(n + 5 \, \vdots \, n + 1\) thì \(4 \, \vdots \, n + 1\)
Hay \(n + 1 \in Ư\left( 4 \right) = \left\{ { \pm 1; \pm 2; \pm 4} \right\}\)
Ta có bảng:

Vậy \(n \in \left\{ { - 5; - 3; - 2;0;1;3} \right\}\)
Có bao nhiêu số nguyên $a < 5$ biết: $10$ là bội của $\left( {2a + 5} \right)$
\(4\)
\(5\)
\(8\)
\(6\)
Đáp án : A
\(10\) là bội của \(2a + 5\) nghĩa là \(2a + 5\) là ước của \(10\)
- Tìm các ước của \(10\)
- Lập bảng tìm \(a,\) đối chiếu điều kiện và kết luận.
Vì \(10\) là bội của \(2a + 5\) nên \(2a + 5\) là ước của \(10\)
\(U\left( {10} \right) = \left\{ { \pm 1; \pm 2; \pm 5; \pm 10} \right\}\)
Ta có bảng:
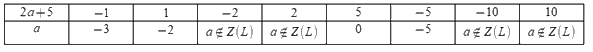
Mà \(a < 5\) nên \(a \in \left\{ { - 3; - 2;0; - 5} \right\}\)
Vậy có \(4\) giá trị nguyên của \(a\) thỏa mãn bài toán.
Tìm $x,$ biết: $x \, \vdots \, 6$ và $24 \, \vdots \, x$
\(x \in \left\{ { \pm 6; \pm 24} \right\}\)
\(x \in \left\{ { \pm 6; \pm 12; \pm 24} \right\}\)
\(x \in \left\{ { \pm 6; \pm 12} \right\}\)
\(\left\{ { \pm 6; \pm 12; \pm 8; \pm 24} \right\}\)
Đáp án : B
- Tìm tập hợp các bội của \(6\)
- Tìm tập hợp các ước của \(24\)
- Lấy giao hai tập trên ta được đáp án.
Ta có:
\(A = B\left( 6 \right) = \left\{ {0; \pm 6; \pm 12; \pm 18; \pm 24;...} \right\}\)
\(B = Ư\left( {24} \right) = \left\{ { \pm 1; \pm 2; \pm 3; \pm 4; \pm 6; \pm 8; \pm 12; \pm 24} \right\}\)
Vậy \(x \in A \cap B = \left\{ { \pm 6; \pm 12; \pm 24} \right\}\)
Cho \(a\) và \(b\) là hai số nguyên khác \(0.\) Biết \(a \, \vdots \, b\) và \(b \, \vdots \, a.\) Khi đó
\(a = b\)
\(a = - b\)
\(a = 2b\)
Cả A, B đều đúng
Đáp án : D
Sử dụng định nghĩa chia hết: \(a \, \vdots \, b\) nếu và chỉ nếu tồn tại số \(q \in Z\) sao cho \(a = b.q\)
Ta có:
\(\begin{array}{l}a \, \vdots \, b \Rightarrow a = b.{q_1}\left( {{q_1} \in Z} \right)\\b \, \vdots \, a \Rightarrow b = a.{q_2}\left( {{q_2} \in Z} \right)\end{array}\)
Suy ra \(a = b.{q_1} = \left( {a.{q_2}} \right).{q_1} = a.\left( {{q_1}{q_2}} \right)\)
Vì \(a \ne 0\) nên \(a = a\left( {{q_1}{q_2}} \right) \Rightarrow 1 = {q_1}{q_2}\)
Mà \({q_1},{q_2} \in Z\) nên \({q_1} = {q_2} = 1\) hoặc \({q_1} = {q_2} = - 1\)
Do đó \(a = b\) hoặc \(a = - b\)
Gọi \(A\) là tập hợp các giá trị $n \in Z$ để \(\left( {{n^2} - 7} \right)\) là bội của \(\left( {n + 3} \right)\). Tổng các phần tử của \(A\) bằng:
\( - 12\)
\( - 10\)
\(0\)
\( - 8\)
Đáp án : A
Biến đổi biểu thức \({n^2} - 7\) về dạng \(a.\left( {n + 3} \right) + b\) với \(b \in Z\) rồi suy ra \(n + 3\) là ước của \(b\)
Ta có:\({n^2} - 7 = {n^2} + 3n - 3n - 9 + 2\)\( = n\left( {n + 3} \right) - 3\left( {n + 3} \right) + 2\)\( = \left( {n - 3} \right)\left( {n + 3} \right) + 2\)
Vì \(n \in Z\) nên để \({n^2} - 7\) là bội của \(n + 3\) thì \(2\) là bội của \(n + 3\) hay \(n + 3\) là ước của \(2\)
\(Ư\left( 2 \right) = \left\{ { \pm 1; \pm 2} \right\}\) nên \(n + 3 \in \left\{ { \pm 1; \pm 2} \right\}\)
Ta có bảng:

Vậy \(n \in A = \left\{ { - 5; - 4; - 2; - 1} \right\}\)
Do đó tổng các phần tử của \(A\) là \(\left( { - 5} \right) + \left( { - 4} \right) + \left( { - 2} \right) + \left( { - 1} \right) = - 12\)
Cho \(x;\,y \in \mathbb{Z}\). Nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) chia hết cho
\(6\)
\(46\)
\(16\)
\(5\)
Đáp án : C
+ Biến đổi để tách \(5x + 46y\) thành tổng của hai số, trong đó một số chia hết cho $16$ và một số chứa nhân tử \(x + 6y\)
+ Sử dụng tính chất chia hết trên tập hợp các số nguyên để chứng minh.
Ta có:
\(\begin{array}{l}5x + 46y = 5x + 30y + 16y\\ = \left( {5x + 30y} \right) + 16y\\ = 5\left( {x + 6y} \right) + 16y\end{array}\)
Vì \(5x + 46y\) chia hết cho $16$ và $16y$ chia hết cho $16$ nên suy ra \(5\left( {x + 6y} \right)\) chia hết cho $16.$
Mà $5$ không chia hết cho $16$ nên suy ra \(x + 6y\) chia hết cho $16$
Vậy nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) cũng chia hết cho $16.$
Có bao nhiêu số nguyên \(n\) thỏa mãn \(\left( {n - 1} \right)\) là bội của \(\left( {n + 5} \right)\) và \(\left( {n + 5} \right)\) là bội của \(\left( {n - 1} \right)?\)
\(0\)
\(2\)
\(1\)
\(3\)
Đáp án : C
Áp dụng: \(b\) chia hết cho \(a\) và \(a\) chia hết cho \(b\) thì \(a\),\(b\) là hai số đối nhau (đã chứng minh từ bài tập trước), từ đó suy ra \(n\).
Vì \(\left( {n - 1} \right)\) là bội của \(\left( {n + 5} \right)\) và \(\left( {n + 5} \right)\) là bội của \(n - 1\),
Nên \(n - 1\) khác \(0\) và \(n + 5\) khác \(0\)
Nên \(n + 5,n - 1\) là hai số đối nhau
Do đó:
\((n + 5) + (n - 1) = 0\)
\(2n + 5 - 1 = 0\)
\(2n + 4 = 0\)
\(2n = -4\)
\(n=-2\)
Vậy có 1 số nguyên n thỏa mãn bài toán.
Trong các phát biểu sau đây, phát biểu nào đúng?
Đáp án : C
Cho \(a,b \in \mathbb{Z}\) và \(b \ne 0\). Nếu có số nguyên \(q\) sao cho \(a = bq\) thì:
Ta nói \(a\) chia hết cho \(b\), kí hiệu là \(a \vdots b\).
Ta có: \( - 18 = \left( { - 6} \right).3\) nên \( - 18\) chia hết cho \( - 6\) => C đúng
Chọn câu sai.
\(\left( { - 19} \right).\left( { - 7} \right) > 0\)
\(3.\left( { - 121} \right) < 0\)
\(45.\left( { - 11} \right) < - 500\)
\(46.\left( { - 11} \right) < - 500\)
Có bao nhiêu số nguyên \(x\) thỏa mãn \(\left( {x - 7} \right)\left( {x + 5} \right) < 0\)?
\(4\)
\(11\)
\(5\)
Không tồn tại \(x\)
Tập hợp các ước của $ - 8$ là:
\(A = \left\{ {1; - 1;2; - 2;4; - 4;8; - 8} \right\}\)
\(A = \left\{ {0; \pm 1; \pm 2 \pm 4 \pm 8} \right\}\)
\(A = \left\{ {1;2;4;8} \right\}\)
\(A = \left\{ {0;1;2;4;8} \right\}\)
Có bao nhiêu ước của \( - 24.\)
$9$
$17$
$8$
$16$
Giá trị lớn nhất của $a$ thỏa mãn $a + 4$ là ước của $9$ là:
$a = 5$
$a = 13$
$a = - 13$
$a = 9$
Cho \(x \in \mathbb{Z}\) và \(\left( { - 154 + x} \right) \vdots \, 3\) thì:
$x$ chia $3$ dư $1$
\(x \, \vdots \, 3\)
$x$ chia $3$ dư $2$
không kết luận được tính chia hết cho $3$ của \(x\)
Tìm $n \in Z,$ biết: $\left( {n{\rm{ }} + 5} \right) \vdots \left( {n{\rm{ }} + 1} \right)$
\(n \in \left\{ { \pm 1; \pm 2 \pm 4} \right\}\)
\(n \in \left\{ { - 5; - 3; - 2;0;1;3} \right\}\)
\(n \in \left\{ {0;1;3} \right\}\)
\(n \in \left\{ { \pm 1; \pm 5} \right\}\)
Có bao nhiêu số nguyên $a < 5$ biết: $10$ là bội của $\left( {2a + 5} \right)$
\(4\)
\(5\)
\(8\)
\(6\)
Tìm $x,$ biết: $x \, \vdots \, 6$ và $24 \, \vdots \, x$
\(x \in \left\{ { \pm 6; \pm 24} \right\}\)
\(x \in \left\{ { \pm 6; \pm 12; \pm 24} \right\}\)
\(x \in \left\{ { \pm 6; \pm 12} \right\}\)
\(\left\{ { \pm 6; \pm 12; \pm 8; \pm 24} \right\}\)
Cho \(a\) và \(b\) là hai số nguyên khác \(0.\) Biết \(a \, \vdots \, b\) và \(b \, \vdots \, a.\) Khi đó
\(a = b\)
\(a = - b\)
\(a = 2b\)
Cả A, B đều đúng
Gọi \(A\) là tập hợp các giá trị $n \in Z$ để \(\left( {{n^2} - 7} \right)\) là bội của \(\left( {n + 3} \right)\). Tổng các phần tử của \(A\) bằng:
\( - 12\)
\( - 10\)
\(0\)
\( - 8\)
Cho \(x;\,y \in \mathbb{Z}\). Nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) chia hết cho
\(6\)
\(46\)
\(16\)
\(5\)
Có bao nhiêu số nguyên \(n\) thỏa mãn \(\left( {n - 1} \right)\) là bội của \(\left( {n + 5} \right)\) và \(\left( {n + 5} \right)\) là bội của \(\left( {n - 1} \right)?\)
\(0\)
\(2\)
\(1\)
\(3\)
Trong các phát biểu sau đây, phát biểu nào đúng?
Chọn câu sai.
\(\left( { - 19} \right).\left( { - 7} \right) > 0\)
\(3.\left( { - 121} \right) < 0\)
\(45.\left( { - 11} \right) < - 500\)
\(46.\left( { - 11} \right) < - 500\)
Đáp án : C
- Tính và kiểm tra các đáp án, sử dụng quy tắc nhân hai số nguyên cùng dấu, khác dấu.
Đáp án A: \(\left( { - 19} \right).\left( { - 7} \right) > 0\) đúng vì tích hai số nguyên cùng dấu là một số nguyên dương.
Đáp án B: \(3.\left( { - 121} \right) < 0\) đúng vì tích hai số nguyên khác dấu là một số nguyên âm.
Đáp án C: \(45.\left( { - 11} \right) = - 495 > - 500\) nên C sai.
Đáp án D: \(46.\left( { - 11} \right) = - 506 < - 500\) nên D đúng.
Có bao nhiêu số nguyên \(x\) thỏa mãn \(\left( {x - 7} \right)\left( {x + 5} \right) < 0\)?
\(4\)
\(11\)
\(5\)
Không tồn tại \(x\)
Đáp án : B
Sử dụng kiến thức \(A.B < 0\) thì \(A\) và \(B\) trái dấu.
\(\left( {x - 7} \right)\left( {x + 5} \right) < 0\) nên \(x - 7\) và \(x + 5\) khác dấu.
Mà \(x + 5 > x - 7\) nên \(x + 5 > 0\) và \(x - 7 < 0\)
Suy ra \(x > - 5\) và \(x < 7\)
Do đó \(x \in \left\{ { - 4, - 3, - 2, - 1,0,1,2,3,4,5,6} \right\}\)
Vậy có \(11\) giá trị nguyên của \(x\) thỏa mãn bài toán.
Tập hợp các ước của $ - 8$ là:
\(A = \left\{ {1; - 1;2; - 2;4; - 4;8; - 8} \right\}\)
\(A = \left\{ {0; \pm 1; \pm 2 \pm 4 \pm 8} \right\}\)
\(A = \left\{ {1;2;4;8} \right\}\)
\(A = \left\{ {0;1;2;4;8} \right\}\)
Đáp án : A
Sử dụng khái niệm bội và ước của một số nguyên:
Nếu $a,b,x \in Z$ và $a = b.x$ thì $a \vdots b$ và $a$ là một bội của $b;b$ là một ước của $a$
Ta có: \( - 8 = - 1.8 = 1.\left( { - 8} \right) = - 2.4 = 2.\left( { - 4} \right)\)
Tập hợp các ước của \( - 8\) là: \(A = \left\{ {1; - 1;2; - 2;4; - 4;8; - 8} \right\}\)
Có bao nhiêu ước của \( - 24.\)
$9$
$17$
$8$
$16$
Đáp án : D
Để tìm tất cả các ước của một số nguyên âm ta chỉ cần tìm tất cả các ước của số đối của số nguyên âm đó. Trước tiên ta tìm ước tự nhiên rồi thêm các ước đối của chúng.
Có \(8\) ước tự nhiên của \(24\) là: \(1;2;3;4;6;8;12;24\)
Có \(8\) ước nguyên âm của \(24\) là: \(-1;-2;-3;-4;-6;-8;-12;-24\)
Vậy có \(8.2 = 16\) ước của \( 24\) nên cũng có $16$ ước của $-24.$
Giá trị lớn nhất của $a$ thỏa mãn $a + 4$ là ước của $9$ là:
$a = 5$
$a = 13$
$a = - 13$
$a = 9$
Đáp án : A
+ Bước 1: Tìm ước của \(9\) + Bước 2: Tìm $a$ và kết luận giá trị lớn nhất của \(a\)
$a + 4$ là ước của $9$ nên $\left( {a + 4} \right) \in Ư\left( 9 \right) = \left\{ { \pm 1; \pm 3; \pm 9} \right\}\;$ Ta có bảng giá trị như sau:

Vậy giá trị lớn nhất của \(a\) là \(a = 5\)
Cho \(x \in \mathbb{Z}\) và \(\left( { - 154 + x} \right) \vdots \, 3\) thì:
$x$ chia $3$ dư $1$
\(x \, \vdots \, 3\)
$x$ chia $3$ dư $2$
không kết luận được tính chia hết cho $3$ của \(x\)
Đáp án : A
Sử dụng tính chất chia hết trong tập hợp các số nguyên $a \, \vdots \, m;b \, \vdots \, m \Rightarrow (a + b) \, \vdots \, m$
Ta có:
\(\left( { - 154 + x} \right) \, \vdots \, 3\)
\(\left( { - 153 - 1 + x} \right) \, \vdots \, 3\)
Suy ra \(\left( {x - 1} \right) \, \vdots \, 3\) (do \( - 153 \, \vdots \, 3\))
Do đó \(x - 1 = 3k \Rightarrow x = 3k + 1\)
Vậy \(x\) chia cho \(3\) dư \(1.\)
Tìm $n \in Z,$ biết: $\left( {n{\rm{ }} + 5} \right) \vdots \left( {n{\rm{ }} + 1} \right)$
\(n \in \left\{ { \pm 1; \pm 2 \pm 4} \right\}\)
\(n \in \left\{ { - 5; - 3; - 2;0;1;3} \right\}\)
\(n \in \left\{ {0;1;3} \right\}\)
\(n \in \left\{ { \pm 1; \pm 5} \right\}\)
Đáp án : B
Bước 1: Phân tích $n + 5$ về dạng $a.\left( {n + 1} \right) + b{\rm{ }}\left( {a,b\; \in \;Z,a \ne 0} \right)$ Bước 2: Tìm $n$
$\left( {n{\rm{ }} + 5} \right) \vdots \left( {n{\rm{ }} + 1} \right)$$ \Rightarrow \left( {n + 1} \right) + 4 \, \vdots \, \left( {n{\rm{ }} + 1} \right)$
Vì \(n + 1 \, \vdots \, n + 1\) và \(n \in Z\) nên để \(n + 5 \, \vdots \, n + 1\) thì \(4 \, \vdots \, n + 1\)
Hay \(n + 1 \in Ư\left( 4 \right) = \left\{ { \pm 1; \pm 2; \pm 4} \right\}\)
Ta có bảng:

Vậy \(n \in \left\{ { - 5; - 3; - 2;0;1;3} \right\}\)
Có bao nhiêu số nguyên $a < 5$ biết: $10$ là bội của $\left( {2a + 5} \right)$
\(4\)
\(5\)
\(8\)
\(6\)
Đáp án : A
\(10\) là bội của \(2a + 5\) nghĩa là \(2a + 5\) là ước của \(10\)
- Tìm các ước của \(10\)
- Lập bảng tìm \(a,\) đối chiếu điều kiện và kết luận.
Vì \(10\) là bội của \(2a + 5\) nên \(2a + 5\) là ước của \(10\)
\(U\left( {10} \right) = \left\{ { \pm 1; \pm 2; \pm 5; \pm 10} \right\}\)
Ta có bảng:
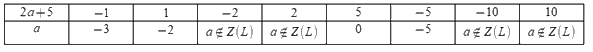
Mà \(a < 5\) nên \(a \in \left\{ { - 3; - 2;0; - 5} \right\}\)
Vậy có \(4\) giá trị nguyên của \(a\) thỏa mãn bài toán.
Tìm $x,$ biết: $x \, \vdots \, 6$ và $24 \, \vdots \, x$
\(x \in \left\{ { \pm 6; \pm 24} \right\}\)
\(x \in \left\{ { \pm 6; \pm 12; \pm 24} \right\}\)
\(x \in \left\{ { \pm 6; \pm 12} \right\}\)
\(\left\{ { \pm 6; \pm 12; \pm 8; \pm 24} \right\}\)
Đáp án : B
- Tìm tập hợp các bội của \(6\)
- Tìm tập hợp các ước của \(24\)
- Lấy giao hai tập trên ta được đáp án.
Ta có:
\(A = B\left( 6 \right) = \left\{ {0; \pm 6; \pm 12; \pm 18; \pm 24;...} \right\}\)
\(B = Ư\left( {24} \right) = \left\{ { \pm 1; \pm 2; \pm 3; \pm 4; \pm 6; \pm 8; \pm 12; \pm 24} \right\}\)
Vậy \(x \in A \cap B = \left\{ { \pm 6; \pm 12; \pm 24} \right\}\)
Cho \(a\) và \(b\) là hai số nguyên khác \(0.\) Biết \(a \, \vdots \, b\) và \(b \, \vdots \, a.\) Khi đó
\(a = b\)
\(a = - b\)
\(a = 2b\)
Cả A, B đều đúng
Đáp án : D
Sử dụng định nghĩa chia hết: \(a \, \vdots \, b\) nếu và chỉ nếu tồn tại số \(q \in Z\) sao cho \(a = b.q\)
Ta có:
\(\begin{array}{l}a \, \vdots \, b \Rightarrow a = b.{q_1}\left( {{q_1} \in Z} \right)\\b \, \vdots \, a \Rightarrow b = a.{q_2}\left( {{q_2} \in Z} \right)\end{array}\)
Suy ra \(a = b.{q_1} = \left( {a.{q_2}} \right).{q_1} = a.\left( {{q_1}{q_2}} \right)\)
Vì \(a \ne 0\) nên \(a = a\left( {{q_1}{q_2}} \right) \Rightarrow 1 = {q_1}{q_2}\)
Mà \({q_1},{q_2} \in Z\) nên \({q_1} = {q_2} = 1\) hoặc \({q_1} = {q_2} = - 1\)
Do đó \(a = b\) hoặc \(a = - b\)
Gọi \(A\) là tập hợp các giá trị $n \in Z$ để \(\left( {{n^2} - 7} \right)\) là bội của \(\left( {n + 3} \right)\). Tổng các phần tử của \(A\) bằng:
\( - 12\)
\( - 10\)
\(0\)
\( - 8\)
Đáp án : A
Biến đổi biểu thức \({n^2} - 7\) về dạng \(a.\left( {n + 3} \right) + b\) với \(b \in Z\) rồi suy ra \(n + 3\) là ước của \(b\)
Ta có:\({n^2} - 7 = {n^2} + 3n - 3n - 9 + 2\)\( = n\left( {n + 3} \right) - 3\left( {n + 3} \right) + 2\)\( = \left( {n - 3} \right)\left( {n + 3} \right) + 2\)
Vì \(n \in Z\) nên để \({n^2} - 7\) là bội của \(n + 3\) thì \(2\) là bội của \(n + 3\) hay \(n + 3\) là ước của \(2\)
\(Ư\left( 2 \right) = \left\{ { \pm 1; \pm 2} \right\}\) nên \(n + 3 \in \left\{ { \pm 1; \pm 2} \right\}\)
Ta có bảng:

Vậy \(n \in A = \left\{ { - 5; - 4; - 2; - 1} \right\}\)
Do đó tổng các phần tử của \(A\) là \(\left( { - 5} \right) + \left( { - 4} \right) + \left( { - 2} \right) + \left( { - 1} \right) = - 12\)
Cho \(x;\,y \in \mathbb{Z}\). Nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) chia hết cho
\(6\)
\(46\)
\(16\)
\(5\)
Đáp án : C
+ Biến đổi để tách \(5x + 46y\) thành tổng của hai số, trong đó một số chia hết cho $16$ và một số chứa nhân tử \(x + 6y\)
+ Sử dụng tính chất chia hết trên tập hợp các số nguyên để chứng minh.
Ta có:
\(\begin{array}{l}5x + 46y = 5x + 30y + 16y\\ = \left( {5x + 30y} \right) + 16y\\ = 5\left( {x + 6y} \right) + 16y\end{array}\)
Vì \(5x + 46y\) chia hết cho $16$ và $16y$ chia hết cho $16$ nên suy ra \(5\left( {x + 6y} \right)\) chia hết cho $16.$
Mà $5$ không chia hết cho $16$ nên suy ra \(x + 6y\) chia hết cho $16$
Vậy nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) cũng chia hết cho $16.$
Có bao nhiêu số nguyên \(n\) thỏa mãn \(\left( {n - 1} \right)\) là bội của \(\left( {n + 5} \right)\) và \(\left( {n + 5} \right)\) là bội của \(\left( {n - 1} \right)?\)
\(0\)
\(2\)
\(1\)
\(3\)
Đáp án : C
Áp dụng: \(b\) chia hết cho \(a\) và \(a\) chia hết cho \(b\) thì \(a\),\(b\) là hai số đối nhau (đã chứng minh từ bài tập trước), từ đó suy ra \(n\).
Vì \(\left( {n - 1} \right)\) là bội của \(\left( {n + 5} \right)\) và \(\left( {n + 5} \right)\) là bội của \(n - 1\),
Nên \(n - 1\) khác \(0\) và \(n + 5\) khác \(0\)
Nên \(n + 5,n - 1\) là hai số đối nhau
Do đó:
\((n + 5) + (n - 1) = 0\)
\(2n + 5 - 1 = 0\)
\(2n + 4 = 0\)
\(2n = -4\)
\(n=-2\)
Vậy có 1 số nguyên n thỏa mãn bài toán.
Trong các phát biểu sau đây, phát biểu nào đúng?
Đáp án : C
Cho \(a,b \in \mathbb{Z}\) và \(b \ne 0\). Nếu có số nguyên \(q\) sao cho \(a = bq\) thì:
Ta nói \(a\) chia hết cho \(b\), kí hiệu là \(a \vdots b\).
Ta có: \( - 18 = \left( { - 6} \right).3\) nên \( - 18\) chia hết cho \( - 6\) => C đúng
Trong chương trình Toán 6 Chân trời sáng tạo, phần kiến thức về phép nhân và phép chia hết hai số nguyên đóng vai trò quan trọng. Việc nắm vững các khái niệm, tính chất và quy tắc liên quan đến hai phép toán này là nền tảng để học tốt các kiến thức toán học ở các lớp trên. Bài viết này sẽ cung cấp một loạt các trắc nghiệm, giúp học sinh ôn tập và đánh giá mức độ hiểu biết của mình về chủ đề này.
Để xác định một số nguyên a chia hết cho một số nguyên b (b ≠ 0), ta cần kiểm tra xem a có thể được viết dưới dạng a = b.k, với k là một số nguyên hay không. Ví dụ: 12 chia hết cho 3 vì 12 = 3.4.
Ước của một số nguyên a là một số nguyên b sao cho a chia hết cho b. Ví dụ: Ước của 12 là: ±1, ±2, ±3, ±4, ±6, ±12.
Bội của một số nguyên a là một số nguyên b sao cho b chia hết cho a. Ví dụ: Bội của 3 là: ..., -6, -3, 0, 3, 6, ...
Các bài toán này thường yêu cầu học sinh vận dụng các kiến thức về tính chia hết, ước và bội để giải quyết các vấn đề thực tế.
Ví dụ 1: Số nào sau đây chia hết cho 5?
Giải: Số 20 chia hết cho 5 vì 20 = 5.4. Vậy đáp án đúng là B.
Ví dụ 2: Tìm tất cả các ước của -18.
Giải: Các ước của -18 là: ±1, ±2, ±3, ±6, ±9, ±18.
Dưới đây là một số bài tập trắc nghiệm để các em luyện tập:
Hy vọng rằng bộ trắc nghiệm này sẽ giúp các em học sinh lớp 6 Chân trời sáng tạo nắm vững kiến thức về phép nhân và phép chia hết hai số nguyên. Chúc các em học tập tốt!