Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 Chân trời sáng tạo tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách giáo khoa và chuyên đề học tập.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Ba lớp 10A, 10B, 10C gồm 128 học sinh cùng tham gia lao động trồng cây. Mỗi học sinh lớp 10A trồng được 3 cây bạch đàn và 4 cây bàng
Hệ nào dưới đây là hệ phương trình bậc nhất ba ẩn? Mỗi bộ ba số (1; 5; 2), (1;1;1) và (-1; 2; 3) có là nghiệm của hệ phương trình bậc nhất ba ẩn đó không?
(1) \(\left\{ \begin{array}{l}4x - 2y + z = 5\\4xz - 5y + 2z = - 7\\ - x + 3y + 2z = 3\end{array} \right.\)
(2) \(\left\{ \begin{array}{l}x + 2z = 5\\2x - y + z = - 1\\3x\; - 2y = - 7\end{array} \right.\)
Phương pháp giải:
Bộ ba số là nghiệm của hệ nếu nó thỏa mãn cả 3 phương trình của hệ.
Lời giải chi tiết:
Hệ phương trình (1) không phải là hệ phương trình bậc nhất vì phương trình thứ hay chứa \(xz\)
Hệ phương trình (2) là hệ phương trình bậc nhất ba ẩn.
+) Bộ ba số (1; 5; 2) là nghiệm của hệ phương trình (2) vì
\(\left\{ \begin{array}{l} 1 + 2.2 = 5\\2.1 - 5 + 2 = - 1\\3.1 - 2.5 = - 7\end{array} \right.\) (nghiệm đún cả ba phương trình của hệ).
+) Bộ ba số (1;1;1) không là nghiệm của hệ phương trình (2) vì \(2.1 - 1 + 1 = 2 \ne - 1\) (không là nghiệm của phương trình \(2x - y + z = - 1\))
+) Bộ ba số (-1; 2; 3) là nghiệm của hệ phương trình (2) vì
\(\left\{ \begin{array}{l} - 1 + 2.3 = 5\\2.( - 1) - 2 + 3 = - 1\\3.( - 1) - 2.2 = - 7\end{array} \right.\) (nghiệm đún cả ba phương trình của hệ).
Ba lớp 10A, 10B, 10C gồm 128 học sinh cùng tham gia lao động trồng cây. Mỗi học sinh lớp 10A trồng được 3 cây bạch đàn và 4 cây bàng. MIỗi học sinh lớp 10B trồng được 2 cây bạch đàn và 5 cây bàng. Mỗi học sinh lớp 10C trồng được 6 cây bạch đàn. Cả 3 lớp trồng được 476 cây bạch đàn và 375 cây bàng. Gọi x, y, = lần lượt là số học sinh của các lớp 10A, 10B,10C.
a) Lập các hệ thức thể hiện mối liên hệ giữa x, y và z.
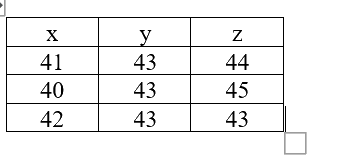
b) Trong bảng dữ liệu sau, chọn các số liệu phủ hợp với số học sinh của mỗi lớp 10A, 10B, 10C và giải thích sự lựa chọn của bạn.
Lời giải chi tiết:
a) Ba lớp có 128 học sinh nên \(x + y + z = 128\)
Số cây bạch đàn mà 3 lớp trồng được là: \(3x + 2y + 6z = 476\)
Số cây bàng mà 3 lớp trồng được là: \(4x + 5y = 375\)
b) Số liệu phù hợp là số liệu thỏa mãn cả 3 liên hệ liệt kê ở ý a).
\(x = 41,y = 43,z = 44\) sai vì số cây bàng là \(4.41 + 5.43 = 379 \ne 375\)
\(x = 40,y = 43,z = 45\) thỏa mãn cả 3 liên hệ trên.
\(x = 42,y = 43,z = 43\) sai vì số cây bàng là \(4.42 + 5.43 = 383 \ne 375\)
Vậy số liệu phù hợp với số học sinh mỗi lớp là \(x = 40,y = 43,z = 45\)
Ba lớp 10A, 10B, 10C gồm 128 học sinh cùng tham gia lao động trồng cây. Mỗi học sinh lớp 10A trồng được 3 cây bạch đàn và 4 cây bàng. MIỗi học sinh lớp 10B trồng được 2 cây bạch đàn và 5 cây bàng. Mỗi học sinh lớp 10C trồng được 6 cây bạch đàn. Cả 3 lớp trồng được 476 cây bạch đàn và 375 cây bàng. Gọi x, y, = lần lượt là số học sinh của các lớp 10A, 10B,10C.
a) Lập các hệ thức thể hiện mối liên hệ giữa x, y và z.
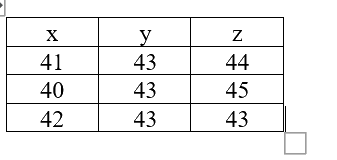
b) Trong bảng dữ liệu sau, chọn các số liệu phủ hợp với số học sinh của mỗi lớp 10A, 10B, 10C và giải thích sự lựa chọn của bạn.
Lời giải chi tiết:
a) Ba lớp có 128 học sinh nên \(x + y + z = 128\)
Số cây bạch đàn mà 3 lớp trồng được là: \(3x + 2y + 6z = 476\)
Số cây bàng mà 3 lớp trồng được là: \(4x + 5y = 375\)
b) Số liệu phù hợp là số liệu thỏa mãn cả 3 liên hệ liệt kê ở ý a).
\(x = 41,y = 43,z = 44\) sai vì số cây bàng là \(4.41 + 5.43 = 379 \ne 375\)
\(x = 40,y = 43,z = 45\) thỏa mãn cả 3 liên hệ trên.
\(x = 42,y = 43,z = 43\) sai vì số cây bàng là \(4.42 + 5.43 = 383 \ne 375\)
Vậy số liệu phù hợp với số học sinh mỗi lớp là \(x = 40,y = 43,z = 45\)
Hệ nào dưới đây là hệ phương trình bậc nhất ba ẩn? Mỗi bộ ba số (1; 5; 2), (1;1;1) và (-1; 2; 3) có là nghiệm của hệ phương trình bậc nhất ba ẩn đó không?
(1) \(\left\{ \begin{array}{l}4x - 2y + z = 5\\4xz - 5y + 2z = - 7\\ - x + 3y + 2z = 3\end{array} \right.\)
(2) \(\left\{ \begin{array}{l}x + 2z = 5\\2x - y + z = - 1\\3x\; - 2y = - 7\end{array} \right.\)
Phương pháp giải:
Bộ ba số là nghiệm của hệ nếu nó thỏa mãn cả 3 phương trình của hệ.
Lời giải chi tiết:
Hệ phương trình (1) không phải là hệ phương trình bậc nhất vì phương trình thứ hay chứa \(xz\)
Hệ phương trình (2) là hệ phương trình bậc nhất ba ẩn.
+) Bộ ba số (1; 5; 2) là nghiệm của hệ phương trình (2) vì
\(\left\{ \begin{array}{l} 1 + 2.2 = 5\\2.1 - 5 + 2 = - 1\\3.1 - 2.5 = - 7\end{array} \right.\) (nghiệm đún cả ba phương trình của hệ).
+) Bộ ba số (1;1;1) không là nghiệm của hệ phương trình (2) vì \(2.1 - 1 + 1 = 2 \ne - 1\) (không là nghiệm của phương trình \(2x - y + z = - 1\))
+) Bộ ba số (-1; 2; 3) là nghiệm của hệ phương trình (2) vì
\(\left\{ \begin{array}{l} - 1 + 2.3 = 5\\2.( - 1) - 2 + 3 = - 1\\3.( - 1) - 2.2 = - 7\end{array} \right.\) (nghiệm đún cả ba phương trình của hệ).
Mục 1 của Chuyên đề học tập Toán 10 - Chân trời sáng tạo thường tập trung vào việc ôn tập và mở rộng kiến thức về tập hợp, các phép toán trên tập hợp, và một số khái niệm cơ bản về logic. Việc nắm vững những kiến thức này là nền tảng quan trọng cho việc học các chương tiếp theo.
Bài tập này yêu cầu học sinh liệt kê các phần tử của một tập hợp cho trước. Để giải bài tập này, học sinh cần hiểu rõ định nghĩa của tập hợp và cách liệt kê các phần tử của tập hợp.
Ví dụ: Cho tập hợp A = {x | x là số tự nhiên nhỏ hơn 10}. Hãy liệt kê các phần tử của tập hợp A.
Lời giải: A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Bài tập này yêu cầu học sinh thực hiện các phép toán trên tập hợp (hợp, giao, hiệu, phần bù). Để giải bài tập này, học sinh cần hiểu rõ định nghĩa và tính chất của các phép toán trên tập hợp.
Ví dụ: Cho tập hợp A = {1, 2, 3} và B = {2, 4, 5}. Hãy tìm A ∪ B, A ∩ B, A \ B.
Lời giải:
Bài tập này yêu cầu học sinh xác định tính đúng sai của một mệnh đề. Để giải bài tập này, học sinh cần hiểu rõ định nghĩa của mệnh đề và cách xác định tính đúng sai của mệnh đề.
Ví dụ: Mệnh đề “Nếu a > b thì a2 > b2” có đúng không?
Lời giải: Mệnh đề này không đúng. Ví dụ, nếu a = 1 và b = -1 thì a > b nhưng a2 = 1 và b2 = 1, do đó a2 không lớn hơn b2.
Để nắm vững kiến thức về Mục 1, các em nên làm thêm nhiều bài tập khác nhau. Các em có thể tìm thấy các bài tập luyện tập trong sách bài tập, trên internet, hoặc trong các đề thi thử.
Mục 1 của Chuyên đề học tập Toán 10 - Chân trời sáng tạo là một phần quan trọng trong chương trình học. Việc nắm vững kiến thức và kỹ năng giải bài tập trong Mục 1 sẽ giúp các em học tốt các chương tiếp theo và đạt kết quả cao trong kỳ thi.