Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 42, 43 Chuyên đề học tập Toán 10 - Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Chúng tôi hiểu rằng việc học toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn các lời giải chi tiết, kèm theo các lưu ý quan trọng để giúp các em hiểu sâu sắc hơn về bài học.
Cho elip (E) có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\) và cho điểm \(M({x_0};{y_0})\) nằm trên (E).
Viết phương trình chính tắc của elip có kích thước của hình chữ nhật cơ sở là 8 và 6. Hãy xác định tọa độ đỉnh, tiêu điểm, tiêu cự, độ dài trục của elip này.
Phương pháp giải:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
+ 4 đỉnh là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right).\)
+ Kích thước của hình chữ nhật cơ sở là 2a và 2b.
+ Tiêu điểm \({F_1}( - c;0),{F_2}(c;0),\)
+ Tiêu cự: \(2c = 2\sqrt {{a^2} - {b^2}} \)
+ Độ dài trục lớn: \(2a\), độ dài trục nhỏ: \(2b\)
Lời giải chi tiết:
Ta có:
+ Kích thước của hình chữ nhật cơ sở là 8 và 6.
\( \Rightarrow \) Độ dài trục lớn: \(2a = 8 \Leftrightarrow a = 4\), độ dài trục nhỏ: \(2b = 6 \Leftrightarrow b = 3\)
Phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\)
+ 4 đỉnh là \({A_1}\left( { - 4;0} \right),{A_2}\left( {4;0} \right),{B_1}\left( {0; - 3} \right),{B_2}\left( {0;3} \right).\)
+ Tiêu điểm \({F_1}( - c;0),{F_2}(c;0),\)
+ Tiêu cự: \(2c = 2\sqrt {{4^2} - {3^2}} = 2\sqrt 7 \)
+ Độ dài trục lớn: \(2a = 8\), độ dài trục nhỏ: \(2b = 6\)
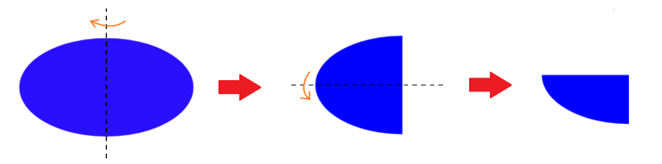
Hãy gấp một mảnh giấy hình elip (Hình 5) thành 4 phần chồng khít lên nhau
Lời giải chi tiết:
Tưởng tượng elip có phương trình chính tắc trên mặt phẳng tọa độ, khi đó ta chỉ cần gập theo các trục tọa độ.
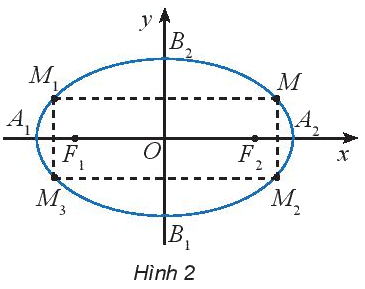
Cho elip (E) có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\) và cho điểm \(M({x_0};{y_0})\) nằm trên (E). Các điểm \({M_1}( - {x_0};{y_0}),{M_2}({x_0}; - {y_0}),{M_3}( - {x_0}; - {y_0})\) có thuộc (E) hay không?
Lời giải chi tiết:
Nếu điểm \(M({x_0};{y_0})\) thuộc elip thì \(\frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1\)
\( \Rightarrow \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} + \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1\)
hay các điểm có tọa độ \({M_1}( - {x_0};{y_0}),{M_2}({x_0}; - {y_0}),{M_3}( - {x_0}; - {y_0})\) cũng thuộc Elip.
Viết phương trình chính tắc của elip có kích thước của hình chữ nhật cơ sở là 8 và 6. Hãy xác định tọa độ đỉnh, tiêu điểm, tiêu cự, độ dài trục của elip này.
Phương pháp giải:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\)
+ 4 đỉnh là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right).\)
+ Kích thước của hình chữ nhật cơ sở là 2a và 2b.
+ Tiêu điểm \({F_1}( - c;0),{F_2}(c;0),\)
+ Tiêu cự: \(2c = 2\sqrt {{a^2} - {b^2}} \)
+ Độ dài trục lớn: \(2a\), độ dài trục nhỏ: \(2b\)
Lời giải chi tiết:
Ta có:
+ Kích thước của hình chữ nhật cơ sở là 8 và 6.
\( \Rightarrow \) Độ dài trục lớn: \(2a = 8 \Leftrightarrow a = 4\), độ dài trục nhỏ: \(2b = 6 \Leftrightarrow b = 3\)
Phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\)
+ 4 đỉnh là \({A_1}\left( { - 4;0} \right),{A_2}\left( {4;0} \right),{B_1}\left( {0; - 3} \right),{B_2}\left( {0;3} \right).\)
+ Tiêu điểm \({F_1}( - c;0),{F_2}(c;0),\)
+ Tiêu cự: \(2c = 2\sqrt {{4^2} - {3^2}} = 2\sqrt 7 \)
+ Độ dài trục lớn: \(2a = 8\), độ dài trục nhỏ: \(2b = 6\)
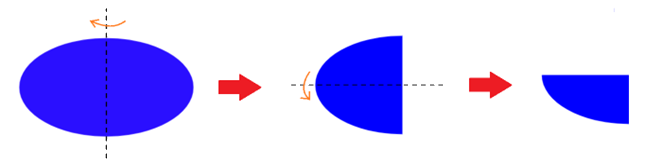
Hãy gấp một mảnh giấy hình elip (Hình 5) thành 4 phần chồng khít lên nhau
Lời giải chi tiết:
Tưởng tượng elip có phương trình chính tắc trên mặt phẳng tọa độ, khi đó ta chỉ cần gập theo các trục tọa độ.
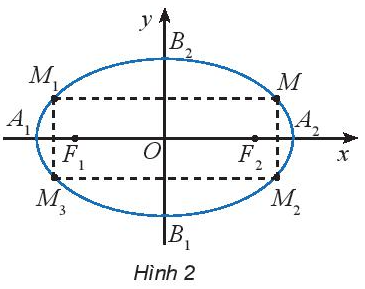
Cho elip (E) có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) \((0 < b < a)\) và cho điểm \(M({x_0};{y_0})\) nằm trên (E). Các điểm \({M_1}( - {x_0};{y_0}),{M_2}({x_0}; - {y_0}),{M_3}( - {x_0}; - {y_0})\) có thuộc (E) hay không?
Lời giải chi tiết:
Nếu điểm \(M({x_0};{y_0})\) thuộc elip thì \(\frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1\)
\( \Rightarrow \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} + \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1\)
hay các điểm có tọa độ \({M_1}( - {x_0};{y_0}),{M_2}({x_0}; - {y_0}),{M_3}( - {x_0}; - {y_0})\) cũng thuộc Elip.
Mục 1 của Chuyên đề học tập Toán 10 - Chân trời sáng tạo thường tập trung vào các khái niệm cơ bản về tập hợp, các phép toán trên tập hợp, và các ứng dụng của tập hợp trong toán học. Việc nắm vững kiến thức nền tảng này là vô cùng quan trọng để học tốt các phần tiếp theo của chương trình.
Dưới đây là lời giải chi tiết cho các bài tập trang 42 và 43 của Chuyên đề học tập Toán 10 - Chân trời sáng tạo:
(Nội dung bài tập 1)
Lời giải:(Giải chi tiết bài tập 1, bao gồm các bước giải và giải thích rõ ràng)
(Nội dung bài tập 2)
Lời giải:(Giải chi tiết bài tập 2, bao gồm các bước giải và giải thích rõ ràng)
(Nội dung bài tập 3)
Lời giải:(Giải chi tiết bài tập 3, bao gồm các bước giải và giải thích rõ ràng)
(Nội dung bài tập 4)
Lời giải:(Giải chi tiết bài tập 4, bao gồm các bước giải và giải thích rõ ràng)
Để giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải bài tập, chúng tôi xin đưa ra một số ví dụ minh họa và bài tập luyện tập:
(Nội dung ví dụ 1)
Lời giải:(Giải chi tiết ví dụ 1)
(Nội dung bài tập luyện tập 1)
Lời giải:(Giải chi tiết bài tập luyện tập 1)
Hy vọng rằng với lời giải chi tiết và các phương pháp giải bài tập được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn trong việc học tập và giải quyết các bài toán liên quan đến tập hợp và các phép toán trên tập hợp trong Chuyên đề học tập Toán 10 - Chân trời sáng tạo. Chúc các em học tốt!