Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 1 trang 39 Chuyên đề học tập Toán 10 – Chân trời sáng tạo. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và phù hợp với chương trình học Toán 10 hiện hành. Hãy cùng theo dõi để nắm vững kiến thức và đạt kết quả tốt nhất!
Khai triển biểu thức:
Đề bài
Khai triển biểu thức:
a) \({(x - 2y)^6}\)
b) \({(3x - 1)^5}\)
Phương pháp giải - Xem chi tiết
Sử dụng công thức nhị thức Newton
\({(a + b)^n} = C_n^0{a^n} + C_n^1{a^{n - 1}}b + ... + C_n^{n - 1}a{b^{n - 1}} + C_n^n{b^n}\)
hoặc tam giác Pascal
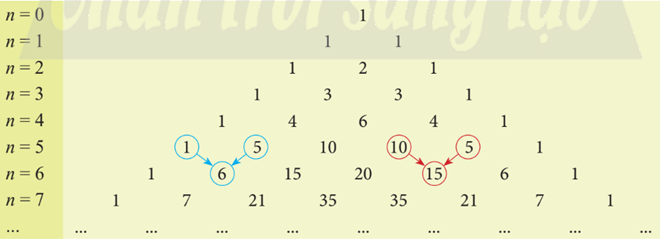
Lời giải chi tiết
a) Sử dụng tam giác Pascal, ta có:
\(\begin{array}{l}{(x + ( - 2y))^6} = {x^6} + 6{x^5}( - 2y) + 15{x^4}{( - 2y)^2} + 20{x^3}{( - 2y)^3} + 15{x^2}{( - 2y)^4} + 6x{( - 2y)^5} + {( - 2y)^6}\\ = {x^6} - 12{x^5}y + 60{x^4}{y^2} - 160{x^3}{y^3} + 240{x^2}{y^4} - 192x{y^5} + 64{y^6}\end{array}\)
b) Sử dụng tam giác Pascal, ta có:
\(\begin{array}{l}{(3x - 1)^5} = {\left( {3x} \right)^5} + 5.{\left( {3x} \right)^4}( - 1) + 10.{\left( {3x} \right)^3}{( - 1)^2} + 10.{\left( {3x} \right)^2}{( - 1)^3} + 5.\left( {3x} \right){( - 1)^4} + {( - 1)^5}\\ = 243{x^5} - 405{x^4} + 270{x^3} - 90{x^2} + 15x - 1\end{array}\)
Bài 1 trang 39 Chuyên đề học tập Toán 10 – Chân trời sáng tạo thuộc chương trình học về hàm số bậc hai. Bài tập này yêu cầu học sinh vận dụng kiến thức về định nghĩa hàm số, tập xác định, tập giá trị, và các tính chất của hàm số bậc hai để giải quyết các bài toán cụ thể.
Bài 1 thường bao gồm các dạng bài tập sau:
Để giải bài 1 trang 39 Chuyên đề học tập Toán 10 – Chân trời sáng tạo một cách hiệu quả, học sinh cần nắm vững các phương pháp sau:
Bài 1a: Cho hàm số f(x) = 2x2 - 5x + 3. Tìm tập xác định và tập giá trị của hàm số.
Lời giải:
Bài 1b: Xác định a, b, c của hàm số y = -x2 + 4x - 1.
Lời giải:
So sánh với dạng tổng quát y = ax2 + bx + c, ta có: a = -1, b = 4, c = -1.
Ví dụ: Tìm hoành độ giao điểm của đồ thị hàm số y = x2 - 3x + 2 với trục hoành.
Lời giải:
Để tìm hoành độ giao điểm của đồ thị hàm số với trục hoành, ta giải phương trình x2 - 3x + 2 = 0. Phương trình này có hai nghiệm là x1 = 1 và x2 = 2. Vậy đồ thị hàm số cắt trục hoành tại hai điểm có hoành độ là 1 và 2.
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số bậc hai, học sinh có thể tự giải các bài tập sau:
Bài 1 trang 39 Chuyên đề học tập Toán 10 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc hai và các ứng dụng của nó. Hy vọng rằng với lời giải chi tiết và phương pháp giải hiệu quả mà Giaitoan.edu.vn cung cấp, các bạn học sinh sẽ tự tin hơn trong việc giải quyết các bài tập tương tự.