Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong Chuyên đề học tập Toán 10 - Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả tốt nhất trong môn Toán.
Cho hypebol (H) với phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) và điểm \(M({x_0};{y_0})\) nằm trên (H). Các điểm \({M_1}( - {x_0};{y_0}),{M_2}({x_0}; - {y_0}),{M_3}( - {x_0}; - {y_0})\) có thuộc (H) không?
Viết phương trình chính tắc của Hypebol có kích thước của hình chữ nhật cơ sở là 8 và 6. Hãy xác định đỉnh, tiêu điểm, tiêu cự, độ dài trục của Hypebol này.
Phương pháp giải:
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
Trong đó:
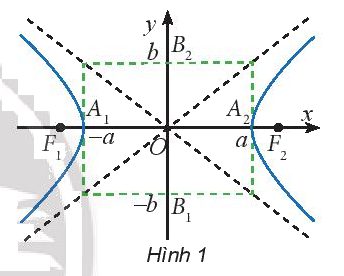
+ 4 đỉnh là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right).\)
+ Kích thước của hình chữ nhật cơ sở là 2a và 2b.
+ Tiêu điểm \({F_1}( - c;0),{F_2}(c;0),\)
+ Tiêu cự: \(2c = 2\sqrt {{a^2} + {b^2}} \)
+ Độ dài trục thực: \(2a\), độ dài trục ảo: \(2b\)
Lời giải chi tiết:
+ Kích thước của hình chữ nhật cơ sở là \(2a = 8\) và \(2b = 6\).
\( \Rightarrow a = 4,b = 3,c = \sqrt {{a^2} + {b^2}} = 5\)
+ 4 đỉnh là \({A_1}\left( { - 4;0} \right),{A_2}\left( {4;0} \right),{B_1}\left( {0; - 3} \right),{B_2}\left( {0;3} \right).\)
+ Tiêu điểm \({F_1}( - 5;0),{F_2}(5;0),\)
+ Tiêu cự: \(2c = 10\)
+ Độ dài trục thực: \(2a = 8\), độ dài trục ảo: \(2b = 6\).
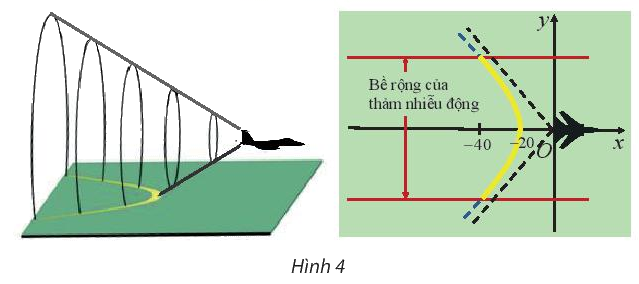
Khi bay với vận tốc siêu thanh (tốc độ chuyển động lớn hơn tốc độ âm thanh trong cùng môi trường), một máy bay tạo ra một vùng nhiễu động trên mặt đất dọc theo một nhánh của hypebol (H) (Hình 4). Phần nghe rõ nhất tiếng ồn của vùng nói trên được gọi là thảm nhiễu động. Bề rộng của thảm này gấp khoảng 5 lần cao độ của máy bay. Tính cao độ của máy bay, biết bề rộng của thảm nhiễu động được đo cách phía sau máy bay một khoảng là 40mile (mile (dặm) là đơn vị đo khoảng cách, 1 mile \( \approx \) 1,6 km) và (H) có phương trình:
\(\frac{{{x^2}}}{{400}} - \frac{{{y^2}}}{{100}} = 1\)
Lời giải chi tiết:
+ Bề rộng của thảm nhiễu động là \(2\left| {{y_M}} \right|\), với \(M \in (H)\) và \({x_M} = - 40\)
+ Cao độ của máy bay: \(h = \frac{{2\left| {{y_M}} \right|}}{5}\)
Lời giải chi tiết
+ Bề rộng của thảm nhiễu động là \(2\left| {{y_M}} \right|\), với \(M \in (H)\) và \({x_M} = - 40\)
\( \Leftrightarrow \frac{{{{( - 40)}^2}}}{{400}} - \frac{{{y_M}^2}}{{100}} = 1 \Leftrightarrow {y_M} = \pm 10\sqrt 3 \)
+ Cao độ của máy bay: \(h = \frac{{2\left| {{y_M}} \right|}}{5} = \frac{{2.10\sqrt 3 }}{5} = 4\sqrt 3 \) (mile) \( \approx 4\sqrt 3 .1,6 \approx 11\) (km).
Cho hypebol (H) với phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) và điểm \(M({x_0};{y_0})\) nằm trên (H). Các điểm \({M_1}( - {x_0};{y_0}),{M_2}({x_0}; - {y_0}),{M_3}( - {x_0}; - {y_0})\) có thuộc (H) không?
Lời giải chi tiết:
Nếu điểm \(M({x_0};{y_0})\) thuộc hypebol thì \(\frac{{{x_0}^2}}{{{a^2}}} - \frac{{{y_0}^2}}{{{b^2}}} = 1\)
\( \Rightarrow \frac{{{{( - {x_0})}^2}}}{{{a^2}}} - \frac{{{y_0}^2}}{{{b^2}}} = 1;\frac{{{x_0}^2}}{{{a^2}}} - \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} - \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1\)
hay các điểm \({M_1}( - {x_0};{y_0}),{M_2}({x_0}; - {y_0}),{M_3}( - {x_0}; - {y_0})\)cũng thuộc Hypebol.
Cho hypebol (H) với phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) và điểm \(M({x_0};{y_0})\) nằm trên (H). Các điểm \({M_1}( - {x_0};{y_0}),{M_2}({x_0}; - {y_0}),{M_3}( - {x_0}; - {y_0})\) có thuộc (H) không?
Lời giải chi tiết:
Nếu điểm \(M({x_0};{y_0})\) thuộc hypebol thì \(\frac{{{x_0}^2}}{{{a^2}}} - \frac{{{y_0}^2}}{{{b^2}}} = 1\)
\( \Rightarrow \frac{{{{( - {x_0})}^2}}}{{{a^2}}} - \frac{{{y_0}^2}}{{{b^2}}} = 1;\frac{{{x_0}^2}}{{{a^2}}} - \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} - \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1\)
hay các điểm \({M_1}( - {x_0};{y_0}),{M_2}({x_0}; - {y_0}),{M_3}( - {x_0}; - {y_0})\)cũng thuộc Hypebol.
Viết phương trình chính tắc của Hypebol có kích thước của hình chữ nhật cơ sở là 8 và 6. Hãy xác định đỉnh, tiêu điểm, tiêu cự, độ dài trục của Hypebol này.
Phương pháp giải:
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
Trong đó:
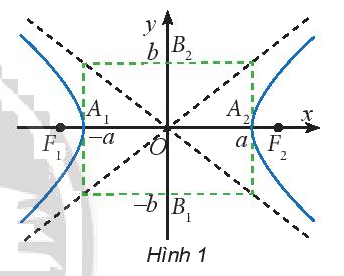
+ 4 đỉnh là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right),{B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right).\)
+ Kích thước của hình chữ nhật cơ sở là 2a và 2b.
+ Tiêu điểm \({F_1}( - c;0),{F_2}(c;0),\)
+ Tiêu cự: \(2c = 2\sqrt {{a^2} + {b^2}} \)
+ Độ dài trục thực: \(2a\), độ dài trục ảo: \(2b\)
Lời giải chi tiết:
+ Kích thước của hình chữ nhật cơ sở là \(2a = 8\) và \(2b = 6\).
\( \Rightarrow a = 4,b = 3,c = \sqrt {{a^2} + {b^2}} = 5\)
+ 4 đỉnh là \({A_1}\left( { - 4;0} \right),{A_2}\left( {4;0} \right),{B_1}\left( {0; - 3} \right),{B_2}\left( {0;3} \right).\)
+ Tiêu điểm \({F_1}( - 5;0),{F_2}(5;0),\)
+ Tiêu cự: \(2c = 10\)
+ Độ dài trục thực: \(2a = 8\), độ dài trục ảo: \(2b = 6\).
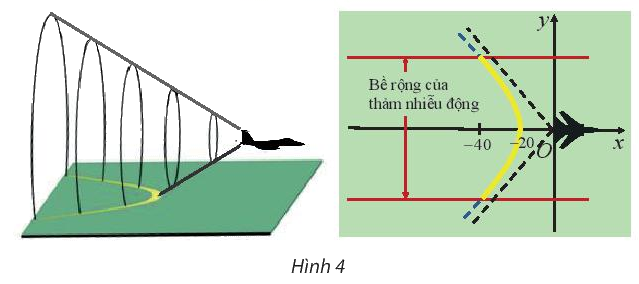
Khi bay với vận tốc siêu thanh (tốc độ chuyển động lớn hơn tốc độ âm thanh trong cùng môi trường), một máy bay tạo ra một vùng nhiễu động trên mặt đất dọc theo một nhánh của hypebol (H) (Hình 4). Phần nghe rõ nhất tiếng ồn của vùng nói trên được gọi là thảm nhiễu động. Bề rộng của thảm này gấp khoảng 5 lần cao độ của máy bay. Tính cao độ của máy bay, biết bề rộng của thảm nhiễu động được đo cách phía sau máy bay một khoảng là 40mile (mile (dặm) là đơn vị đo khoảng cách, 1 mile \( \approx \) 1,6 km) và (H) có phương trình:
\(\frac{{{x^2}}}{{400}} - \frac{{{y^2}}}{{100}} = 1\)
Lời giải chi tiết:
+ Bề rộng của thảm nhiễu động là \(2\left| {{y_M}} \right|\), với \(M \in (H)\) và \({x_M} = - 40\)
+ Cao độ của máy bay: \(h = \frac{{2\left| {{y_M}} \right|}}{5}\)
Lời giải chi tiết
+ Bề rộng của thảm nhiễu động là \(2\left| {{y_M}} \right|\), với \(M \in (H)\) và \({x_M} = - 40\)
\( \Leftrightarrow \frac{{{{( - 40)}^2}}}{{400}} - \frac{{{y_M}^2}}{{100}} = 1 \Leftrightarrow {y_M} = \pm 10\sqrt 3 \)
+ Cao độ của máy bay: \(h = \frac{{2\left| {{y_M}} \right|}}{5} = \frac{{2.10\sqrt 3 }}{5} = 4\sqrt 3 \) (mile) \( \approx 4\sqrt 3 .1,6 \approx 11\) (km).
Mục 1 của Chuyên đề học tập Toán 10 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và kỹ năng giải bài tập liên quan. Trang 50 và 51 thường chứa các bài tập vận dụng và mở rộng, giúp học sinh củng cố kiến thức đã học và phát triển tư duy toán học.
Để giải quyết các bài tập trên trang 50, trước tiên, học sinh cần xác định rõ kiến thức lý thuyết liên quan. Ví dụ, nếu bài tập liên quan đến hàm số bậc hai, học sinh cần nhớ lại các khái niệm về tập xác định, tập giá trị, đỉnh của parabol, và các phương pháp tìm nghiệm của phương trình bậc hai.
Tương tự như trang 50, việc giải các bài tập trên trang 51 đòi hỏi học sinh phải nắm vững kiến thức lý thuyết và kỹ năng giải bài tập. Tuy nhiên, các bài tập trên trang 51 có thể có độ khó cao hơn, đòi hỏi học sinh phải vận dụng kiến thức một cách linh hoạt và sáng tạo.
Để giải bài tập Toán 10 - Chân trời sáng tạo một cách hiệu quả, học sinh có thể áp dụng các phương pháp sau:
Trong quá trình học Toán 10 - Chân trời sáng tạo, học sinh cần lưu ý những điều sau:
Việc giải bài tập mục 1 trang 50, 51 Chuyên đề học tập Toán 10 - Chân trời sáng tạo đòi hỏi sự kiên trì, nỗ lực và phương pháp học tập đúng đắn. Hy vọng rằng với những hướng dẫn chi tiết và phương pháp giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, bạn sẽ tự tin chinh phục môn Toán và đạt kết quả tốt nhất.