Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong sách Chuyên đề học tập Toán 10 - Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu hỗ trợ tối đa cho học sinh, chúng tôi đã biên soạn bộ giải bài tập này, tập trung vào việc giải thích rõ ràng từng bước, giúp bạn nắm vững phương pháp và tự tin giải quyết các bài toán tương tự.
Chứng tỏ rằng nếu điểm \(M({x_0};{y_0})\) nằm trên parabol (P) thì điểm \(N({x_0}; - {y_0})\) cũng nằm trên parabol (P)
Trong mặt phẳng Oxy, cho điểm \(A(2;0)\) và đường thẳng \(d:x + 2 = 0\). Viết phương trình của đường (L) là tập hợp các tâm \(J(x;y)\) của các đường tròn (C) thay đổi nhưng luôn luôn đi qua A và tiếp xúc với d.
Lời giải chi tiết:
Ta có: (C) đi qua \(A(2;0)\) và tiếp xúc với \(d:x + 2 = 0\)
\(\begin{array}{l} \Rightarrow d(J,d) = JA\\ \Leftrightarrow \left| {x + 2} \right| = \sqrt {{{(x - 2)}^2} + {y^2}} \\ \Leftrightarrow {\left( {x + 2} \right)^2} = {(x - 2)^2} + {y^2}\\ \Leftrightarrow {x^2} + 4x + 4 = {x^2} - 4x + 4 + {y^2}\\ \Leftrightarrow {y^2} = 8x\end{array}\)
Tức là tâm \(J(x;y)\) của (C) nằm trên parabol (P) \({y^2} = 8x\)
Tìm tọa độ tiêu điểm, tọa độ đỉnh, phương trình đường chuẩn và trục đối xứng của các parabol sau:
a) \(({P_1}):{y^2} = 2x\)
b) \(({P_2}):{y^2} = x\)
c) \(({P_3}):{y^2} = \frac{1}{5}x\)
Phương pháp giải:
Cho parabol có PTCT \({y^2} = 2px\)
+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)
+ Đỉnh O(0;0)
+ Đường chuẩn: \(\Delta :x = - \frac{p}{2}\)
+ Trục đối xứng: Ox
Lời giải chi tiết:
a) Ta có: \(2p = 2\), suy ra \(p = 1\).
Vậy \(({P_1})\) có tiêu điểm \(F\left( {\frac{1}{2};0} \right)\), đỉnh \(O(0;0)\), đường chuẩn \(\Delta :x = - \frac{1}{2}\) và nhận Ox làm trục đối xứng.
b) Ta có: \(2p = 1\), suy ra \(p = \frac{1}{2}\).
Vậy \(({P_2})\) có tiêu điểm \(F\left( {\frac{1}{4};0} \right)\), đỉnh \(O(0;0)\), đường chuẩn \(\Delta :x = - \frac{1}{4}\) và nhận Ox làm trục đối xứng.
c) Ta có: \(2p = \frac{1}{5}\), suy ra \(p = \frac{1}{{10}}\).
Vậy \(({P_2})\) có tiêu điểm \(F\left( {\frac{1}{{20}};0} \right)\), đỉnh \(O(0;0)\), đường chuẩn \(\Delta :x = - \frac{1}{{20}}\) và nhận Ox làm trục đối xứng.
Chứng tỏ rằng nếu điểm \(M({x_0};{y_0})\) nằm trên parabol (P) thì điểm \(N({x_0}; - {y_0})\) cũng nằm trên parabol (P)
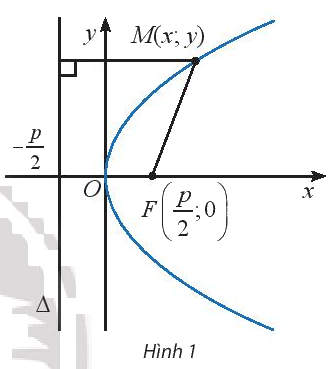
Lời giải chi tiết:
Nếu điểm \(M({x_0};{y_0})\) nằm trên parabol thì \({y_0}^2 = 2p{x_0} \Leftrightarrow {( - {y_0})^2} = 2p{x_0}\)
nên điểm \(M'({x_0}; - {y_0})\) cũng nằm trên parabol.
Chứng tỏ rằng nếu điểm \(M({x_0};{y_0})\) nằm trên parabol (P) thì điểm \(N({x_0}; - {y_0})\) cũng nằm trên parabol (P)
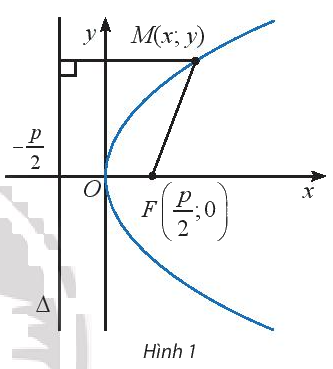
Lời giải chi tiết:
Nếu điểm \(M({x_0};{y_0})\) nằm trên parabol thì \({y_0}^2 = 2p{x_0} \Leftrightarrow {( - {y_0})^2} = 2p{x_0}\)
nên điểm \(M'({x_0}; - {y_0})\) cũng nằm trên parabol.
Tìm tọa độ tiêu điểm, tọa độ đỉnh, phương trình đường chuẩn và trục đối xứng của các parabol sau:
a) \(({P_1}):{y^2} = 2x\)
b) \(({P_2}):{y^2} = x\)
c) \(({P_3}):{y^2} = \frac{1}{5}x\)
Phương pháp giải:
Cho parabol có PTCT \({y^2} = 2px\)
+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)
+ Đỉnh O(0;0)
+ Đường chuẩn: \(\Delta :x = - \frac{p}{2}\)
+ Trục đối xứng: Ox
Lời giải chi tiết:
a) Ta có: \(2p = 2\), suy ra \(p = 1\).
Vậy \(({P_1})\) có tiêu điểm \(F\left( {\frac{1}{2};0} \right)\), đỉnh \(O(0;0)\), đường chuẩn \(\Delta :x = - \frac{1}{2}\) và nhận Ox làm trục đối xứng.
b) Ta có: \(2p = 1\), suy ra \(p = \frac{1}{2}\).
Vậy \(({P_2})\) có tiêu điểm \(F\left( {\frac{1}{4};0} \right)\), đỉnh \(O(0;0)\), đường chuẩn \(\Delta :x = - \frac{1}{4}\) và nhận Ox làm trục đối xứng.
c) Ta có: \(2p = \frac{1}{5}\), suy ra \(p = \frac{1}{{10}}\).
Vậy \(({P_2})\) có tiêu điểm \(F\left( {\frac{1}{{20}};0} \right)\), đỉnh \(O(0;0)\), đường chuẩn \(\Delta :x = - \frac{1}{{20}}\) và nhận Ox làm trục đối xứng.
Trong mặt phẳng Oxy, cho điểm \(A(2;0)\) và đường thẳng \(d:x + 2 = 0\). Viết phương trình của đường (L) là tập hợp các tâm \(J(x;y)\) của các đường tròn (C) thay đổi nhưng luôn luôn đi qua A và tiếp xúc với d.
Lời giải chi tiết:
Ta có: (C) đi qua \(A(2;0)\) và tiếp xúc với \(d:x + 2 = 0\)
\(\begin{array}{l} \Rightarrow d(J,d) = JA\\ \Leftrightarrow \left| {x + 2} \right| = \sqrt {{{(x - 2)}^2} + {y^2}} \\ \Leftrightarrow {\left( {x + 2} \right)^2} = {(x - 2)^2} + {y^2}\\ \Leftrightarrow {x^2} + 4x + 4 = {x^2} - 4x + 4 + {y^2}\\ \Leftrightarrow {y^2} = 8x\end{array}\)
Tức là tâm \(J(x;y)\) của (C) nằm trên parabol (P) \({y^2} = 8x\)
Mục 1 của Chuyên đề học tập Toán 10 - Chân trời sáng tạo thường tập trung vào các khái niệm cơ bản và ứng dụng của chúng. Việc nắm vững kiến thức nền tảng là vô cùng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Mục 1 thường bao gồm các nội dung sau:
Trang 56 thường chứa các bài tập vận dụng kiến thức về định nghĩa hàm số và tập xác định. Để giải các bài tập này, bạn cần xác định rõ các yếu tố của hàm số và kiểm tra xem giá trị nào của biến độc lập làm cho mẫu số bằng 0 hoặc biểu thức dưới dấu căn bậc chẵn âm.
Ví dụ: Cho hàm số f(x) = √(x - 2). Xác định tập xác định của hàm số.
Giải: Để hàm số f(x) xác định, ta cần có x - 2 ≥ 0, suy ra x ≥ 2. Vậy tập xác định của hàm số là [2, +∞).
Trang 57 thường chứa các bài tập về các loại hàm số cơ bản. Để giải các bài tập này, bạn cần nắm vững các tính chất của từng loại hàm số và sử dụng các công thức liên quan.
Ví dụ: Cho hàm số y = 2x + 1. Tìm điểm thuộc đồ thị hàm số có tung độ bằng 5.
Giải: Thay y = 5 vào phương trình hàm số, ta có 5 = 2x + 1, suy ra 2x = 4, do đó x = 2. Vậy điểm cần tìm là (2, 5).
Trang 58 thường chứa các bài tập ứng dụng của hàm số. Để giải các bài tập này, bạn cần đọc kỹ đề bài, xác định các yếu tố liên quan đến hàm số và xây dựng phương trình hoặc hệ phương trình phù hợp.
Ví dụ: Một người nông dân có 100m hàng rào để rào một khu vườn hình chữ nhật. Hỏi khu vườn đó có diện tích lớn nhất là bao nhiêu?
Giải: Gọi chiều dài và chiều rộng của khu vườn lần lượt là x và y. Ta có 2(x + y) = 100, suy ra x + y = 50. Diện tích của khu vườn là S = xy. Thay y = 50 - x vào công thức tính diện tích, ta có S = x(50 - x) = 50x - x2. Để tìm diện tích lớn nhất, ta tìm giá trị lớn nhất của hàm số S(x) = 50x - x2. Hàm số này đạt giá trị lớn nhất khi x = 25, và giá trị lớn nhất là S(25) = 50(25) - 252 = 625.
Để học tốt môn Toán, bạn cần:
Hy vọng với bộ giải bài tập này, bạn sẽ học tập tốt hơn và đạt kết quả cao trong môn Toán.