Giải mục 2 trang 35, 36, 37 Chuyên đề học tập Toán 10 - Chân trời sáng tạo

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong Chuyên đề học tập Toán 10 - Chân trời sáng tạo.

Chúng tôi hiểu rằng việc tự học Toán đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ gia sư giàu kinh nghiệm của chúng tôi đã biên soạn bộ giải đáp này để giúp bạn nắm vững kiến thức và tự tin giải quyết các bài toán.

Có thể dự đoán rằng, với mỗi \(n \in \mathbb{N}*\), \(\begin{array}{l}C_n^k = C_n^{n - k}\quad \quad \quad (0 \le k \le n)\quad (2)\\C_n^{k - 1} + C_n^k = C_{n + 1}^k\quad (1 \le k \le n)\quad (3)\end{array}\) Hãy chứng minh các công thức trên.

HĐ Khám phá 2

Từ các đẳng thức như

\(\begin{array}{l}C_3^0 = C_3^3 = 1,\quad C_4^1 = C_4^3 = 4,\\C_3^0 + C_3^1 = C_4^1,\quad C_4^2 + C_4^3 = C_5^3,\end{array}\)

Có thể dự đoán rằng, với mỗi \(n \in \mathbb{N}*\),

\(\begin{array}{l}C_n^k = C_n^{n - k}\quad \quad \quad (0 \le k \le n)\quad (2)\\C_n^{k - 1} + C_n^k = C_{n + 1}^k\quad (1 \le k \le n)\quad (3)\end{array}\)

Hãy chứng minh các công thức trên.

Gợi ý: Sử dụng công thức \(C_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}},n \in \mathbb{N},0 \le k \le n.\)

Lời giải chi tiết:

\(C_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}} = \frac{{n!}}{{\left( {n - k} \right)!k!}} = \frac{{n!}}{{\left( {n - k} \right)!\left[ {n - (n - k)} \right]!}} = C_n^{n - k}\)

\(\begin{array}{l}C_n^{k - 1} + C_n^k = \frac{{n!}}{{(k - 1)!\left( {n - k + 1} \right)!}} + \frac{{n!}}{{k!\left( {n - k} \right)!}}\\ = \frac{{n!}}{{k!\left( {n + 1 - k} \right)!}}\left( {k + \left( {n + 1 - k} \right)} \right)\\ = \frac{{(n + 1)!}}{{k!\left( {n + 1 - k} \right)!}} = C_{n + 1}^k\end{array}\)

Lựa chọn câu để xem lời giải nhanh hơn

HĐ Khám phá 2
Thực hành 2

Từ các đẳng thức như

\(\begin{array}{l}C_3^0 = C_3^3 = 1,\quad C_4^1 = C_4^3 = 4,\\C_3^0 + C_3^1 = C_4^1,\quad C_4^2 + C_4^3 = C_5^3,\end{array}\)

Có thể dự đoán rằng, với mỗi \(n \in \mathbb{N}*\),

\(\begin{array}{l}C_n^k = C_n^{n - k}\quad \quad \quad (0 \le k \le n)\quad (2)\\C_n^{k - 1} + C_n^k = C_{n + 1}^k\quad (1 \le k \le n)\quad (3)\end{array}\)

Hãy chứng minh các công thức trên.

Gợi ý: Sử dụng công thức \(C_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}},n \in \mathbb{N},0 \le k \le n.\)

Lời giải chi tiết:

\(C_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}} = \frac{{n!}}{{\left( {n - k} \right)!k!}} = \frac{{n!}}{{\left( {n - k} \right)!\left[ {n - (n - k)} \right]!}} = C_n^{n - k}\)

Sử dụng tam giác Pascal, hãy khai triển:

a) \({(2x + 1)^6}\)

b) \({(x - y)^7}\)

Phương pháp giải:

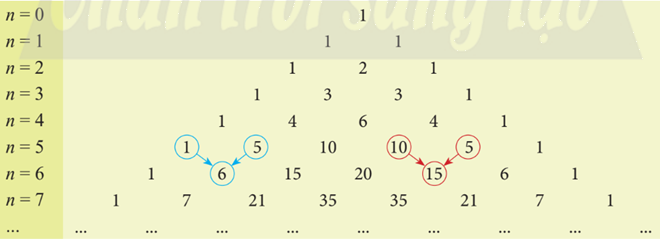
Giải mục 2 trang 35, 36, 37 Chuyên đề học tập Toán 10 - Chân trời sáng tạo 1

Lời giải chi tiết:

a) Sử dụng tam giác Pascal, ta có:

\(\begin{array}{l}{(2x + 1)^6} = {\left( {2x} \right)^6} + 6{\left( {2x} \right)^5} + 15{\left( {2x} \right)^4} + 20{\left( {2x} \right)^3} + 15{\left( {2x} \right)^2} + 6.2x + 1\\ = 64{x^6} + 192{x^5} + 240{x^4} + 160{x^3} + 60{x^2} + 12x + 1\end{array}\)

b) Sử dụng tam giác Pascal, ta có:

\(\begin{array}{l}{(x + ( - y))^7} = {x^7} + 7{x^6}( - y) + 21{x^5}{( - y)^2} + 35{x^4}{( - y)^3} + 35{x^3}{( - y)^4} + 21{x^2}{( - y)^5} + 7x{( - y)^6} + {( - y)^7}\\ = {x^7} - 7{x^6}y + 21{x^5}{y^2} - 35{x^4}{y^3} + 35{x^3}{y^4} - 21{x^2}{y^5} + 7x{y^6} - {y^7}\end{array}\)

Thực hành 2

Sử dụng tam giác Pascal, hãy khai triển:

a) \({(2x + 1)^6}\)

b) \({(x - y)^7}\)

Phương pháp giải:

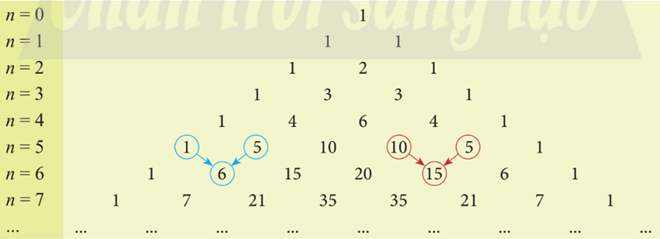
Giải mục 2 trang 35, 36, 37 Chuyên đề học tập Toán 10 - Chân trời sáng tạo 1 1

Lời giải chi tiết:

a) Sử dụng tam giác Pascal, ta có:

b) Sử dụng tam giác Pascal, ta có:

Xây dựng nền tảng Toán THPT vững vàng từ hôm nay! Đừng bỏ lỡ Giải mục 2 trang 35, 36, 37 Chuyên đề học tập Toán 10 - Chân trời sáng tạo đặc sắc thuộc chuyên mục bài tập toán lớp 10 trên nền tảng học toán. Với bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chương trình Toán lớp 10, đây chính là "kim chỉ nam" giúp các em tối ưu hóa ôn luyện, củng cố kiến thức cốt lõi và chuẩn bị hành trang vững chắc cho tương lai. Phương pháp học trực quan, logic sẽ mang lại hiệu quả vượt trội trên lộ trình chinh phục đại học!

Giải mục 2 trang 35, 36, 37 Chuyên đề học tập Toán 10 - Chân trời sáng tạo: Hướng dẫn chi tiết

Mục 2 của Chuyên đề học tập Toán 10 - Chân trời sáng tạo thường tập trung vào các khái niệm và bài tập liên quan đến một chủ đề cụ thể. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết cơ bản và rèn luyện kỹ năng giải toán thường xuyên.

Nội dung chính của Mục 2

Trước khi đi vào giải chi tiết các bài tập trang 35, 36, 37, chúng ta cần xác định nội dung chính của Mục 2. Thông thường, mục này sẽ bao gồm:

Các định nghĩa, định lý quan trọng.
Các ví dụ minh họa cách áp dụng lý thuyết vào thực tế.
Các bài tập vận dụng, bài tập nâng cao để kiểm tra mức độ hiểu bài.