Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 44 Chuyên đề học tập Toán 10 - Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn là địa chỉ tin cậy dành cho các em học sinh cần hỗ trợ giải toán online. Chúng tôi luôn cập nhật lời giải mới nhất, chính xác nhất và dễ hiểu nhất.
Cho điểm \(M(x;y)\)nằm trên elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có hai tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\) (Hình 6).
a) Tính độ dài hai bán kính qua tiêu của điểm \(M(x,y)\) trên (E): \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{36}} = 1\)
b) Tìm các điểm trên elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có độ dài hai bán kính qua tiêu bằng nhau.
Phương pháp giải:
Cho PTCT: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Độ dài bán kính qua tiêu của điểm \(M(x,y)\) trên (E) là:
\(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x.\)
Lời giải chi tiết:
a) Ta có: \({a^2} = 64,{b^2} = 36 \Rightarrow a = 8,b = 6 \Rightarrow c = \sqrt {{a^2} - {b^2}} = 2\sqrt 7 \)
Độ dài hai bán kính qua tiêu của điểm \(M(x,y)\) là:
\(M{F_1} = 8 + \frac{{\sqrt 7 }}{4}x;M{F_2} = 8 - \frac{{\sqrt 7 }}{4}x.\)
b) Độ dài bán kính qua tiêu của điểm \(M(x,y)\) trên (E) là:
\(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x.\)
Để độ dài hai bán kính qua tiêu bằng nhau thì \(a + \frac{c}{a}x = a - \frac{c}{a}x\)
\( \Leftrightarrow \frac{c}{a}x = - \frac{c}{a}x \Leftrightarrow x = 0\)
Mà \(M(x,y) \in (E)\) \( \Rightarrow \frac{{{y^2}}}{{{b^2}}} = 1 \Leftrightarrow y = \pm b\)
Vậy tại các điểm \({B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right)\) thì độ dài hai bán kính qua tiêu bằng nhau.
Cho điểm \(M(x;y)\)nằm trên elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có hai tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\) (Hình 6).
a) Tính \({F_1}{M^2}\) và \({F_2}{M^2}\) theo \(x,y,c.\)
b) Chứng tỏ rằng \({F_1}{M^2} - {F_2}{M^2} = 4cx,\;{F_1}M - {F_2}M = 2\frac{{cx}}{a}\)
c) Tính độ dài hai đoạn \(M{F_1},M{F_2}\) theo \(a,c,x.\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {M{F_1}} ( - c - x; - y);\overrightarrow {M{F_2}} (c - x; - y)\)
\( \Rightarrow M{F_1}^2 = {( - c - x)^2} + {( - y)^2};M{F_2}^2 = {(c - x)^2} + {( - y)^2}\)
b) \({F_1}{M^2} - {F_2}{M^2} = {( - c - x)^2} - {(c - x)^2} = 4cx\)
Mà \({F_1}M + {F_2}M = 2a\) (do \(M \in (E)\))
\( \Rightarrow \;{F_1}M - {F_2}M = \frac{{{F_1}{M^2} - {F_2}{M^2}}}{{{F_1}M + {F_2}M}} = 2\frac{{cx}}{a}\)
c)
\(\begin{array}{l}M{F_1} = \frac{{2a + \frac{{2c}}{a}x}}{2} = a + \frac{c}{a}x\\M{F_2} = \frac{{2a - \frac{{2c}}{a}x}}{2} = a - \frac{c}{a}x\end{array}\)
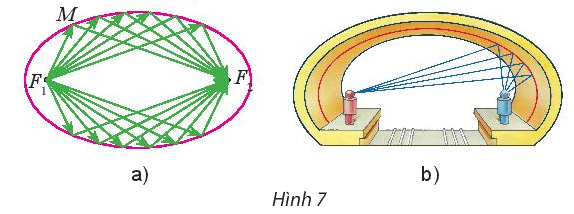
Người ta chứng minh được rằng ánh sáng hay âm thanh đi từ một tiêu điểm, khi đến một điểm M bất kì trên elip luôn luôn cho tia phản xạ đi qua tiêu điểm còn lại, nghĩa là đi theo các bán kính qua tiêu (Hình 7a).
Vòm xe điện ngầm của một thành phố có mặt cát hình elip (Hình 7b). Hãy giải thích tại sao tiếng nói của một người phát ra từ một tiêu điểm bên này, mặc dù khi đi đến các điểm khác nhau trên elip vẫn luôn dội lại tới tiêu điểm bên kia cùng một lúc.
Phương pháp giải:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Với M bất kì thuộc Elip, ta luôn có: \(M{F_1} + M{F_2} = 2a\)
Lời giải chi tiết:
Gọi PTCT của elip biểu diễn vòm xe điện ngầm là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Với M bất kì thuộc Elip, ta luôn có: \(M{F_1} + M{F_2} = 2a\)
Nói cách khác tiếng nói phát ra từ một tiêu điểm bên này, khi đi đến các điểm khác nhau trên elip vẫn luôn tới tiêu điểm bên kia với cùng một quãng đường là \(2a\).
Do đó tiếng nói vẫn luôn dội lại tới tiêu điểm bên kia cùng một lúc.
Cho điểm \(M(x;y)\)nằm trên elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có hai tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\) (Hình 6).
a) Tính \({F_1}{M^2}\) và \({F_2}{M^2}\) theo \(x,y,c.\)
b) Chứng tỏ rằng \({F_1}{M^2} - {F_2}{M^2} = 4cx,\;{F_1}M - {F_2}M = 2\frac{{cx}}{a}\)
c) Tính độ dài hai đoạn \(M{F_1},M{F_2}\) theo \(a,c,x.\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {M{F_1}} ( - c - x; - y);\overrightarrow {M{F_2}} (c - x; - y)\)
\( \Rightarrow M{F_1}^2 = {( - c - x)^2} + {( - y)^2};M{F_2}^2 = {(c - x)^2} + {( - y)^2}\)
b) \({F_1}{M^2} - {F_2}{M^2} = {( - c - x)^2} - {(c - x)^2} = 4cx\)
Mà \({F_1}M + {F_2}M = 2a\) (do \(M \in (E)\))
\( \Rightarrow \;{F_1}M - {F_2}M = \frac{{{F_1}{M^2} - {F_2}{M^2}}}{{{F_1}M + {F_2}M}} = 2\frac{{cx}}{a}\)
c)
\(\begin{array}{l}M{F_1} = \frac{{2a + \frac{{2c}}{a}x}}{2} = a + \frac{c}{a}x\\M{F_2} = \frac{{2a - \frac{{2c}}{a}x}}{2} = a - \frac{c}{a}x\end{array}\)
a) Tính độ dài hai bán kính qua tiêu của điểm \(M(x,y)\) trên (E): \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{36}} = 1\)
b) Tìm các điểm trên elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có độ dài hai bán kính qua tiêu bằng nhau.
Phương pháp giải:
Cho PTCT: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Độ dài bán kính qua tiêu của điểm \(M(x,y)\) trên (E) là:
\(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x.\)
Lời giải chi tiết:
a) Ta có: \({a^2} = 64,{b^2} = 36 \Rightarrow a = 8,b = 6 \Rightarrow c = \sqrt {{a^2} - {b^2}} = 2\sqrt 7 \)
Độ dài hai bán kính qua tiêu của điểm \(M(x,y)\) là:
\(M{F_1} = 8 + \frac{{\sqrt 7 }}{4}x;M{F_2} = 8 - \frac{{\sqrt 7 }}{4}x.\)
b) Độ dài bán kính qua tiêu của điểm \(M(x,y)\) trên (E) là:
\(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x.\)
Để độ dài hai bán kính qua tiêu bằng nhau thì \(a + \frac{c}{a}x = a - \frac{c}{a}x\)
\( \Leftrightarrow \frac{c}{a}x = - \frac{c}{a}x \Leftrightarrow x = 0\)
Mà \(M(x,y) \in (E)\) \( \Rightarrow \frac{{{y^2}}}{{{b^2}}} = 1 \Leftrightarrow y = \pm b\)
Vậy tại các điểm \({B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right)\) thì độ dài hai bán kính qua tiêu bằng nhau.
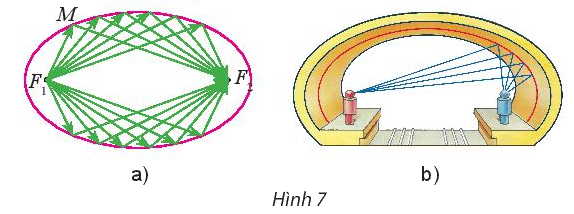
Người ta chứng minh được rằng ánh sáng hay âm thanh đi từ một tiêu điểm, khi đến một điểm M bất kì trên elip luôn luôn cho tia phản xạ đi qua tiêu điểm còn lại, nghĩa là đi theo các bán kính qua tiêu (Hình 7a).
Vòm xe điện ngầm của một thành phố có mặt cát hình elip (Hình 7b). Hãy giải thích tại sao tiếng nói của một người phát ra từ một tiêu điểm bên này, mặc dù khi đi đến các điểm khác nhau trên elip vẫn luôn dội lại tới tiêu điểm bên kia cùng một lúc.
Phương pháp giải:
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Với M bất kì thuộc Elip, ta luôn có: \(M{F_1} + M{F_2} = 2a\)
Lời giải chi tiết:
Gọi PTCT của elip biểu diễn vòm xe điện ngầm là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Với M bất kì thuộc Elip, ta luôn có: \(M{F_1} + M{F_2} = 2a\)
Nói cách khác tiếng nói phát ra từ một tiêu điểm bên này, khi đi đến các điểm khác nhau trên elip vẫn luôn tới tiêu điểm bên kia với cùng một quãng đường là \(2a\).
Do đó tiếng nói vẫn luôn dội lại tới tiêu điểm bên kia cùng một lúc.
Mục 2 trang 44 trong Chuyên đề học tập Toán 10 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết cơ bản, hiểu rõ các định nghĩa, định lý và công thức liên quan. Việc ôn tập kiến thức nền tảng là bước quan trọng trước khi bắt đầu giải bài tập.
Mục 2 trang 44 thường bao gồm các dạng bài tập khác nhau, đòi hỏi học sinh phải vận dụng linh hoạt kiến thức đã học. Dưới đây là phân tích chi tiết từng dạng bài tập thường gặp:
Loại bài tập này yêu cầu học sinh áp dụng trực tiếp định nghĩa và tính chất của các khái niệm đã học để giải quyết vấn đề. Ví dụ, bài tập yêu cầu tính giá trị của biểu thức, chứng minh đẳng thức, hoặc xác định điều kiện của biến.
Các bài tập này đòi hỏi học sinh phải hiểu rõ và vận dụng thành thạo các định lý và công thức đã học để giải quyết các bài toán phức tạp hơn. Ví dụ, bài tập yêu cầu tính độ dài đoạn thẳng, góc, diện tích, hoặc thể tích.
Đây là dạng bài tập khó hơn, yêu cầu học sinh phải kết hợp kiến thức từ nhiều chương khác nhau để giải quyết vấn đề. Ví dụ, bài tập yêu cầu giải phương trình, bất phương trình, hoặc hệ phương trình.
Để giúp các em học sinh hiểu rõ hơn về cách giải các bài tập trong Mục 2 trang 44, chúng tôi sẽ cung cấp lời giải chi tiết cho từng bài tập. Lời giải sẽ bao gồm các bước giải cụ thể, giải thích rõ ràng và dễ hiểu.
Bài tập 1: (Ví dụ về một bài tập cụ thể và lời giải chi tiết)
Bài tập 2: (Ví dụ về một bài tập cụ thể và lời giải chi tiết)
Bài tập 3: (Ví dụ về một bài tập cụ thể và lời giải chi tiết)
Kiến thức trong Mục 2 trang 44 có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau của toán học và thực tế. Ví dụ, kiến thức về hàm số được sử dụng để mô tả và phân tích các hiện tượng tự nhiên, kinh tế, xã hội. Kiến thức về phương trình và bất phương trình được sử dụng để giải quyết các bài toán tối ưu hóa và ra quyết định.
Để nâng cao kiến thức và kỹ năng giải toán, các em học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng bài viết này đã cung cấp cho các em học sinh những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong Mục 2 trang 44 Chuyên đề học tập Toán 10 - Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao!