Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong Chuyên đề học tập Toán 10 - Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu hỗ trợ tối đa cho học sinh, chúng tôi đã biên soạn và kiểm tra kỹ lưỡng lời giải cho từng bài tập trong mục 1 trang 26, 27, 28, 29.
Bằng cách tô màu trên lưới ô vuông như hình dưới đây
Chứng minh rằng đẳng thức sau đúng với mọi \(n \in \mathbb{N}*\)
\(1 + 2 + 3 + ... + n = \frac{{n(n + 1)}}{2}\)
Phương pháp giải:
Chứng minh mệnh đề đúng với \(n \ge p\) thì:
Bước 1: Kiểm tra mệnh đề là đúng với \(n = p\)
Bước 2: Giả thiết mệnh đề đúng với số tự nhiên \(n = k \ge p\) và chứng minh mệnh đề đúng với \(n = k + 1.\) Kết luận.
Lời giải chi tiết:
Ta chứng minh bằng quy nạp theo n.
Bước 1: Với \(n = 1\) ta có \(1 = \frac{{1(1 + 1)}}{2}\)
Như vậy mệnh đề đúng cho trường hợp \(n = 1\)
Bước 2: Giả sử mệnh đề đúng với \(n = k\), nghĩa là có:
\(1 + 2 + 3 + ... + k = \frac{{k(k + 1)}}{2}\)
Ta sẽ chứng minh mệnh đề cũng đúng với \(n = k + 1\), nghĩa là cần chứng minh
\(1 + 2 + 3 + ... + k + (k + 1) = \frac{{(k + 1)(k + 2)}}{2}\)
Thật vậy ta có
\(\begin{array}{l}1 + 2 + 3 + ... + k + (k + 1) = \frac{{k(k + 1)}}{2} + (k + 1)\\ = \frac{{k(k + 1) + 2(k + 1)}}{2} = \frac{{(k + 1)(k + 2)}}{2}\end{array}\)
Vậy mệnh đề đúng với mọi số tự nhiên \(n \ge 1\)
Chứng minh rằng bất đẳng thức sau đúng với mọi số tự nhiên \(n \ge 3\)
\({2^{n + 1}} > {n^2} + n + 2\)
Phương pháp giải:
Chứng minh mệnh đề đúng với \(n \ge p\) thì:
Bước 1: Kiểm tra mệnh đề là đúng với \(n = p\)
Bước 2: Giả thiết mệnh đề đúng với số tự nhiên \(n = k \ge p\) và chứng minh mệnh đề đúng với \(n = k + 1.\) Kết luận.
Lời giải chi tiết:
Ta chứng minh bằng quy nạp theo n.
Bước 1: Với \(n = 3\) ta có \({2^{3 + 1}} > {3^2} + 3 + 2\)
Như vậy mệnh đề đúng cho trường hợp \(n = 3\)
Bước 2: Giả sử mệnh đề đúng với \(n = k\), nghĩa là có:
\({2^{k + 1}} > {k^2} + k + 2\)
Ta sẽ chứng minh bất đẳng thức đúng với \(n = k + 1\), nghĩa là cần chứng minh
\({2^{k + 1 + 1}} > {(k + 1)^2} + k + 1 + 2\)
Sử dụng giả thiết quy nạp, với lưu ý \(k \ge 3\), ta có
\(\begin{array}{l}{2^{k + 1 + 1}} = {2.2^{k + 1}}\\\quad \quad > 2({k^2} + k + 2) = {(k + 1)^2} + {k^2} + 1 + 2\\\quad \quad > {(k + 1)^2} + k + 1 + 2\end{array}\)
Vậy bất đẳng thức đúng với \(n = k + 1\).
Theo nguyên lí quy nạp toán học, bất đẳng thức đúng với mọi số tự nhiên \(n \ge 3\).
Bằng cách tô màu trên lưới ô vuông như hình dưới đây,
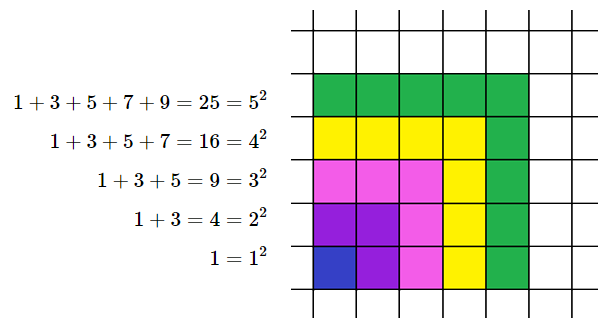
Một học sinh phát hiện ra công thức sau:
\(1 + 3 + 5 + ... + (2n - 1) = {n^2}\quad (1)\)
a) Hãy chỉ ra công thức (1) đúng với \(n = 1,2,3,4,5.\)
b) Từ việc tô màu trên lưới ô vuông như Hình 1, bạn học sinh khẳng định rằng công thức (1) chắc chắn đúng với mọi số tự nhiên \(n \ge 1\). Khẳng định như vậy đã thuyết phục chưa? Tại sao?
Lời giải chi tiết:
a) Kiểm tra bằng tính toán trực tiếp. Ta có
\(1 = {1^2}\) nên (1) đúng với \(n = 1\)
\(1 + 3 = 4 = {2^2}\) nên (1) đúng với \(n = 2\)
\(1 + 3 + 5 = 9 = {3^2}\) nên (1) đúng với \(n = 3\)
\(1 + 3 + 5 + 7 = 16 = {4^2}\) nên (1) đúng với \(n = 4\)
\(1 + 3 + 5 + 7 + 9 = 25 = {5^2}\) nên (1) đúng với \(n = 5\)
b) Khẳng định của bạn HS chỉ là phỏng đoán. Việc tô màu hay tính toán trực tiếp không thể kiểm chứng hết tất cả các giá trị của n (mà chỉ kiểm chứng được một số hữu hạn giá trị n nào đó). Do đó khẳng định của bạn HS là chưa thuyết phục.
Bằng cách tô màu trên lưới ô vuông như hình dưới đây,
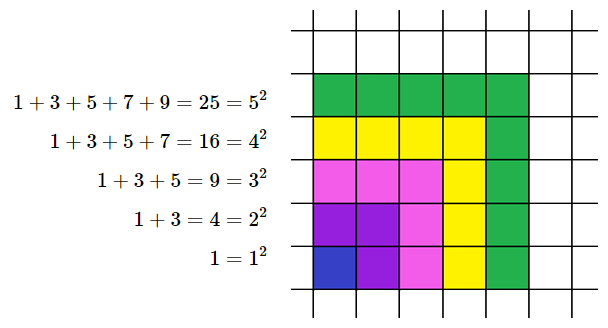
Một học sinh phát hiện ra công thức sau:
\(1 + 3 + 5 + ... + (2n - 1) = {n^2}\quad (1)\)
a) Hãy chỉ ra công thức (1) đúng với \(n = 1,2,3,4,5.\)
b) Từ việc tô màu trên lưới ô vuông như Hình 1, bạn học sinh khẳng định rằng công thức (1) chắc chắn đúng với mọi số tự nhiên \(n \ge 1\). Khẳng định như vậy đã thuyết phục chưa? Tại sao?
Lời giải chi tiết:
a) Kiểm tra bằng tính toán trực tiếp. Ta có
\(1 = {1^2}\) nên (1) đúng với \(n = 1\)
\(1 + 3 = 4 = {2^2}\) nên (1) đúng với \(n = 2\)
\(1 + 3 + 5 = 9 = {3^2}\) nên (1) đúng với \(n = 3\)
\(1 + 3 + 5 + 7 = 16 = {4^2}\) nên (1) đúng với \(n = 4\)
\(1 + 3 + 5 + 7 + 9 = 25 = {5^2}\) nên (1) đúng với \(n = 5\)
b) Khẳng định của bạn HS chỉ là phỏng đoán. Việc tô màu hay tính toán trực tiếp không thể kiểm chứng hết tất cả các giá trị của n (mà chỉ kiểm chứng được một số hữu hạn giá trị n nào đó). Do đó khẳng định của bạn HS là chưa thuyết phục.
Chứng minh rằng đẳng thức sau đúng với mọi \(n \in \mathbb{N}*\)
\(1 + 2 + 3 + ... + n = \frac{{n(n + 1)}}{2}\)
Phương pháp giải:
Chứng minh mệnh đề đúng với \(n \ge p\) thì:
Bước 1: Kiểm tra mệnh đề là đúng với \(n = p\)
Bước 2: Giả thiết mệnh đề đúng với số tự nhiên \(n = k \ge p\) và chứng minh mệnh đề đúng với \(n = k + 1.\) Kết luận.
Lời giải chi tiết:
Ta chứng minh bằng quy nạp theo n.
Bước 1: Với \(n = 1\) ta có \(1 = \frac{{1(1 + 1)}}{2}\)
Như vậy mệnh đề đúng cho trường hợp \(n = 1\)
Bước 2: Giả sử mệnh đề đúng với \(n = k\), nghĩa là có:
\(1 + 2 + 3 + ... + k = \frac{{k(k + 1)}}{2}\)
Ta sẽ chứng minh mệnh đề cũng đúng với \(n = k + 1\), nghĩa là cần chứng minh
\(1 + 2 + 3 + ... + k + (k + 1) = \frac{{(k + 1)(k + 2)}}{2}\)
Thật vậy ta có
\(\begin{array}{l}1 + 2 + 3 + ... + k + (k + 1) = \frac{{k(k + 1)}}{2} + (k + 1)\\ = \frac{{k(k + 1) + 2(k + 1)}}{2} = \frac{{(k + 1)(k + 2)}}{2}\end{array}\)
Vậy mệnh đề đúng với mọi số tự nhiên \(n \ge 1\)
Chứng minh rằng bất đẳng thức sau đúng với mọi số tự nhiên \(n \ge 3\)
\({2^{n + 1}} > {n^2} + n + 2\)
Phương pháp giải:
Chứng minh mệnh đề đúng với \(n \ge p\) thì:
Bước 1: Kiểm tra mệnh đề là đúng với \(n = p\)
Bước 2: Giả thiết mệnh đề đúng với số tự nhiên \(n = k \ge p\) và chứng minh mệnh đề đúng với \(n = k + 1.\) Kết luận.
Lời giải chi tiết:
Ta chứng minh bằng quy nạp theo n.
Bước 1: Với \(n = 3\) ta có \({2^{3 + 1}} > {3^2} + 3 + 2\)
Như vậy mệnh đề đúng cho trường hợp \(n = 3\)
Bước 2: Giả sử mệnh đề đúng với \(n = k\), nghĩa là có:
\({2^{k + 1}} > {k^2} + k + 2\)
Ta sẽ chứng minh bất đẳng thức đúng với \(n = k + 1\), nghĩa là cần chứng minh
\({2^{k + 1 + 1}} > {(k + 1)^2} + k + 1 + 2\)
Sử dụng giả thiết quy nạp, với lưu ý \(k \ge 3\), ta có
\(\begin{array}{l}{2^{k + 1 + 1}} = {2.2^{k + 1}}\\\quad \quad > 2({k^2} + k + 2) = {(k + 1)^2} + {k^2} + 1 + 2\\\quad \quad > {(k + 1)^2} + k + 1 + 2\end{array}\)
Vậy bất đẳng thức đúng với \(n = k + 1\).
Theo nguyên lí quy nạp toán học, bất đẳng thức đúng với mọi số tự nhiên \(n \ge 3\).
Mục 1 của Chuyên đề học tập Toán 10 - Chân trời sáng tạo thường tập trung vào việc ôn tập và mở rộng kiến thức về các khái niệm cơ bản như tập hợp, số thực, và các phép toán trên số thực. Việc nắm vững kiến thức nền tảng này là vô cùng quan trọng để học tốt các chương trình Toán học nâng cao hơn.
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 1, trang 26, 27, 28, 29 của Chuyên đề học tập Toán 10 - Chân trời sáng tạo:
Để giải tốt các bài tập trong Mục 1, bạn cần nắm vững các kiến thức cơ bản về tập hợp, số thực, và các phép toán trên số thực. Ngoài ra, bạn cũng cần rèn luyện kỹ năng tư duy logic và khả năng vận dụng kiến thức vào giải quyết các bài toán thực tế.
Kiến thức về tập hợp và số thực có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học, như:
| Lĩnh vực | Ứng dụng |
|---|---|
| Tin học | Biểu diễn dữ liệu, thuật toán. |
| Kinh tế | Phân tích thị trường, dự báo xu hướng. |
| Vật lý | Mô tả các đại lượng vật lý, giải các bài toán động lực học. |
Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập hiệu quả, bạn sẽ học tốt Mục 1 của Chuyên đề học tập Toán 10 - Chân trời sáng tạo. Chúc bạn thành công!