Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 Chân trời sáng tạo tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho mục 2 trang 55, 56, 57, 58, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho các em những bài giải chính xác, khoa học và phù hợp với chương trình học.
Cho điểm \(M(x;y)\) trên parabol (P) \({y^2} = 2px\) (Hình 2). Tính khoảng cách từ điểm M đến tiêu điểm \(F\) của (P).
Tính bán kính qua tiêu của điểm dưới đây trên parabol tương ứng.
a) Điểm \({M_1}(1; - 4)\) trên \(({P_1}):{y^2} = 16x\)
b) Điểm \({M_2}(3; - 3)\) trên \(({P_2}):{y^2} = 3x\)
c) Điểm \({M_3}(4;1)\) trên \(({P_3}):{y^2} = \frac{1}{4}x\)
Phương pháp giải:
Cho parabol có phương trình chính tắc \({y^2} = 2px\)
+) Với \(M({x_0};{y_0})\) thuộc parabol, bán kính qua tiêu: \(FM = {x_0} + \frac{p}{2}\)
Lời giải chi tiết:
a) \(({P_1}):{y^2} = 16x\)
Ta có \(2p = 16\), suy ra \(p = 8\). Vậy độ dài bán kính qua tiêu của điểm \({M_1}(1; - 4)\) là: \(FM = x + \frac{p}{2} = 1 + \frac{8}{2} = 5.\)
b) \(({P_2}):{y^2} = 3x\)
Ta có \(2p = 3\), suy ra \(p = \frac{3}{2}\). Vậy độ dài bán kính qua tiêu của điểm \({M_2}(3; - 3)\) là: \(FM = x + \frac{p}{2} = 3 + \frac{{\frac{3}{2}}}{2} = \frac{{15}}{4}.\)
c) \(({P_3}):{y^2} = \frac{1}{4}x\)
Ta có \(2p = \frac{1}{4}\), suy ra \(p = \frac{1}{8}\). Vậy độ dài bán kính qua tiêu của điểm \({M_3}(4;1)\) là: \(FM = x + \frac{p}{2} = 4 + \frac{{\frac{1}{8}}}{2} = \frac{{65}}{{16}}.\)
Mặt cắt của một chảo ăng-ten có dạng một parabol (P) có phương trình chính tắc \({y^2} = 0,25x\). Biết đầu thu tín hiệu của chảo ăng-ten tại tiêu điểm F của (P). Tính khoảng cách từ điểm \(M(0,25;0,25)\) trên ăng-ten đến F.
Phương pháp giải:
Cho parabol có phương trình chính tắc \({y^2} = 2px\)
+) Tiêu điểm \(F(\frac{p}{2};0)\)
Lời giải chi tiết:
(P) \({y^2} = 0,25x\) có \(2p = 0,25 \Leftrightarrow p = \frac{1}{8}\)
Khoảng cách từ điểm \(M(0,25;0,25)\) trên ăng-ten đến \(F\) là:
\(MF = {x_M} + \frac{p}{2} = 0,25 + \frac{{\frac{1}{8}}}{2} = 0,3125\)
Một cổng có dạng một đường parabol (P). Biết chiều cao của cổng là 7,6 m và khoảng cách giữa hai chân cổng là 9m. Người ta muốn treo một ngôi sao tại tiêu điểm F của (P) bằng một đoạn dây nối từ đỉnh S của cổn. Tính khoảng cách từ tâm ngôi sao đến đỉnh cổng.
Phương pháp giải:
Cho parabol có phương trình chính tắc \({y^2} = 2px\)
+) Tiêu điểm \(F(\frac{p}{2};0)\)
Lời giải chi tiết:
Gọi phương trình chính tắc của parabol là: \({y^2} = 2px\)
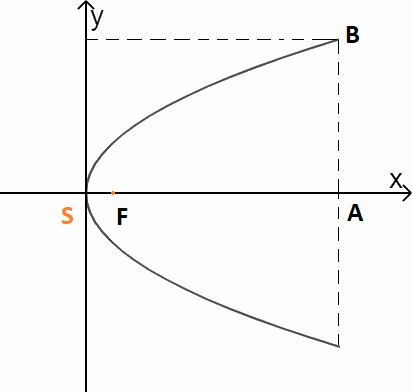
Chiều cao của cổng là 7,6 m nên \(A(7,6;0)\)
Khoản cách giữa hai chân cổng là 9m nên \(B(7,6;4,5)\)
\(B \in (P)\) suy ra \(4,{5^2} = 2p.7,6 \Rightarrow p = \frac{{405}}{{304}}\)
Tiêu điểm F của (P) có tọa độ: \(F\left( {\frac{{405}}{{608}};0} \right)\)
Hay khoảng cách từ tâm ngôi sao đến đỉnh cổng là \(\frac{{405}}{{608}} \approx 0,67(m)\),
Cho điểm \(M(x;y)\) trên parabol (P) \({y^2} = 2px\) (Hình 2). Tính khoảng cách từ điểm M đến tiêu điểm \(F\) của (P).
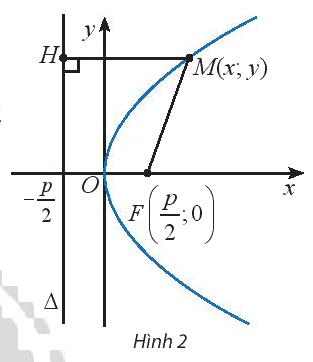
Lời giải chi tiết:
Tiêu điểm \(F(\frac{p}{2};0)\)
Ta có:
\(MF = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + 2p{x_0}} = \sqrt {{{\left( {x + \frac{p}{2}} \right)}^2}} = x + \frac{p}{2}\);
Cho điểm \(M(x;y)\) trên parabol (P) \({y^2} = 2px\) (Hình 2). Tính khoảng cách từ điểm M đến tiêu điểm \(F\) của (P).
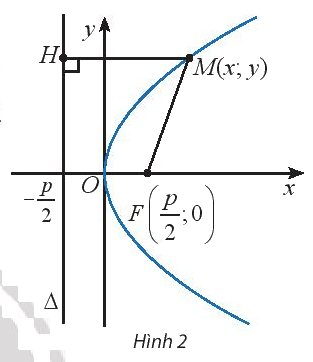
Lời giải chi tiết:
Tiêu điểm \(F(\frac{p}{2};0)\)
Ta có:
\(MF = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + 2p{x_0}} = \sqrt {{{\left( {x + \frac{p}{2}} \right)}^2}} = x + \frac{p}{2}\);
Tính bán kính qua tiêu của điểm dưới đây trên parabol tương ứng.
a) Điểm \({M_1}(1; - 4)\) trên \(({P_1}):{y^2} = 16x\)
b) Điểm \({M_2}(3; - 3)\) trên \(({P_2}):{y^2} = 3x\)
c) Điểm \({M_3}(4;1)\) trên \(({P_3}):{y^2} = \frac{1}{4}x\)
Phương pháp giải:
Cho parabol có phương trình chính tắc \({y^2} = 2px\)
+) Với \(M({x_0};{y_0})\) thuộc parabol, bán kính qua tiêu: \(FM = {x_0} + \frac{p}{2}\)
Lời giải chi tiết:
a) \(({P_1}):{y^2} = 16x\)
Ta có \(2p = 16\), suy ra \(p = 8\). Vậy độ dài bán kính qua tiêu của điểm \({M_1}(1; - 4)\) là: \(FM = x + \frac{p}{2} = 1 + \frac{8}{2} = 5.\)
b) \(({P_2}):{y^2} = 3x\)
Ta có \(2p = 3\), suy ra \(p = \frac{3}{2}\). Vậy độ dài bán kính qua tiêu của điểm \({M_2}(3; - 3)\) là: \(FM = x + \frac{p}{2} = 3 + \frac{{\frac{3}{2}}}{2} = \frac{{15}}{4}.\)
c) \(({P_3}):{y^2} = \frac{1}{4}x\)
Ta có \(2p = \frac{1}{4}\), suy ra \(p = \frac{1}{8}\). Vậy độ dài bán kính qua tiêu của điểm \({M_3}(4;1)\) là: \(FM = x + \frac{p}{2} = 4 + \frac{{\frac{1}{8}}}{2} = \frac{{65}}{{16}}.\)
Một cổng có dạng một đường parabol (P). Biết chiều cao của cổng là 7,6 m và khoảng cách giữa hai chân cổng là 9m. Người ta muốn treo một ngôi sao tại tiêu điểm F của (P) bằng một đoạn dây nối từ đỉnh S của cổn. Tính khoảng cách từ tâm ngôi sao đến đỉnh cổng.
Phương pháp giải:
Cho parabol có phương trình chính tắc \({y^2} = 2px\)
+) Tiêu điểm \(F(\frac{p}{2};0)\)
Lời giải chi tiết:
Gọi phương trình chính tắc của parabol là: \({y^2} = 2px\)
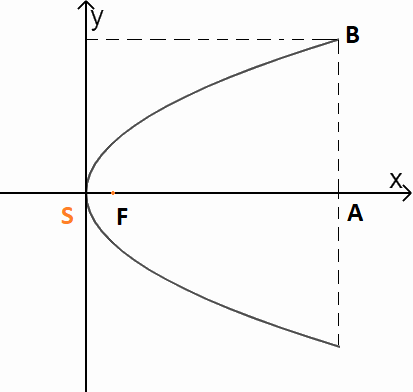
Chiều cao của cổng là 7,6 m nên \(A(7,6;0)\)
Khoản cách giữa hai chân cổng là 9m nên \(B(7,6;4,5)\)
\(B \in (P)\) suy ra \(4,{5^2} = 2p.7,6 \Rightarrow p = \frac{{405}}{{304}}\)
Tiêu điểm F của (P) có tọa độ: \(F\left( {\frac{{405}}{{608}};0} \right)\)
Hay khoảng cách từ tâm ngôi sao đến đỉnh cổng là \(\frac{{405}}{{608}} \approx 0,67(m)\),
Mặt cắt của một chảo ăng-ten có dạng một parabol (P) có phương trình chính tắc \({y^2} = 0,25x\). Biết đầu thu tín hiệu của chảo ăng-ten tại tiêu điểm F của (P). Tính khoảng cách từ điểm \(M(0,25;0,25)\) trên ăng-ten đến F.
Phương pháp giải:
Cho parabol có phương trình chính tắc \({y^2} = 2px\)
+) Tiêu điểm \(F(\frac{p}{2};0)\)
Lời giải chi tiết:
(P) \({y^2} = 0,25x\) có \(2p = 0,25 \Leftrightarrow p = \frac{1}{8}\)
Khoảng cách từ điểm \(M(0,25;0,25)\) trên ăng-ten đến \(F\) là:
\(MF = {x_M} + \frac{p}{2} = 0,25 + \frac{{\frac{1}{8}}}{2} = 0,3125\)
Mục 2 của Chuyên đề học tập Toán 10 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và kỹ năng giải bài tập liên quan. Việc giải các bài tập trang 55, 56, 57, 58 là bước quan trọng để củng cố kiến thức và chuẩn bị cho các bài kiểm tra, thi cử.
Các bài tập trang 55 thường xoay quanh việc áp dụng các định nghĩa, định lý đã học để giải quyết các bài toán cơ bản. Ví dụ, có thể là bài tập về xác định các yếu tố của một hàm số, vẽ đồ thị hàm số, hoặc tìm tập xác định của hàm số.
Trang 56 thường nâng cao độ khó hơn một chút, yêu cầu học sinh phải kết hợp nhiều kiến thức khác nhau để giải quyết bài toán. Có thể là bài tập về tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số, hoặc giải phương trình, bất phương trình chứa hàm số.
Các bài tập trang 57 có thể liên quan đến các ứng dụng thực tế của hàm số, ví dụ như bài toán về quỹ đạo chuyển động, bài toán về tối ưu hóa trong kinh tế, hoặc bài toán về thống kê.
Trang 58 thường là phần bài tập tổng hợp, yêu cầu học sinh phải vận dụng tất cả các kiến thức đã học để giải quyết các bài toán phức tạp. Đây là cơ hội để học sinh rèn luyện kỹ năng tư duy logic, phân tích và giải quyết vấn đề.
Bài tập: Tìm tập xác định của hàm số y = √(x - 2) / (x + 1)
Giải:
Để học tập hiệu quả, các em cần:
Việc giải các bài tập mục 2 trang 55, 56, 57, 58 Chuyên đề học tập Toán 10 - Chân trời sáng tạo là một phần quan trọng trong quá trình học tập môn Toán. Hy vọng với những hướng dẫn chi tiết và phương pháp giải hiệu quả mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong việc giải quyết các bài toán và đạt kết quả tốt trong học tập.