Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 52, 53 của Chuyên đề học tập Toán 10 - Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài toán phức tạp.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi đã biên soạn lời giải đầy đủ, kèm theo các bước giải thích rõ ràng, giúp học sinh nắm vững kiến thức và phương pháp giải bài tập.
Cho điểm (M(x;y))nằm trên hypebol (H): (frac{{{x^2}}}{{{a^2}}} - frac{{{y^2}}}{{{b^2}}} = 1)
Tính độ dài hai bán kính qua tiêu của điểm \(M(x;y)\) trên hypebol (H): \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\)
Phương pháp giải:
Cho điểm \(M(x;y)\)nằm trên hypebol (H): \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
Độ dài hai bán kính qua tiêu của điểm \(M(x;y)\) là:
\(M{F_1} = \left| {a + \frac{c}{a}x} \right|;M{F_2} = \left| {a - \frac{c}{a}x} \right|\)
Lời giải chi tiết:
Hypebol (H): \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\) có \(a = 8,b = 6\) suy ra \(c = \sqrt {{a^2} + {b^2}} = 10\).
Độ dài hai bán kính qua tiêu của điểm \(M(x;y)\) là:
\(M{F_1} = \left| {a + \frac{c}{a}x} \right| = \left| {8 + \frac{3}{4}x} \right|;M{F_2} = \left| {a - \frac{c}{a}x} \right| = \left| {8 - \frac{3}{4}x} \right|\)
Tính độ dài hai bán kính qua tiêu của đỉnh \({A_2}(a;0)\) trên hypebol (H): \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
Phương pháp giải:
Cho điểm \(M(x;y)\)nằm trên hypebol (H): \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
Độ dài hai bán kính qua tiêu của điểm \(M(x;y)\) là:
\(M{F_1} = \left| {a + \frac{c}{a}x} \right|;M{F_2} = \left| {a - \frac{c}{a}x} \right|\)
Lời giải chi tiết:
Độ dài hai bán kính qua tiêu của điểm \({A_2}(a;0)\) trên (H) là:
\(M{F_1} = \left| {a + \frac{c}{a}x} \right| = \left| {a + \frac{c}{a}a} \right| = a + c;M{F_2} = \left| {a - \frac{c}{a}x} \right| = \left| {a - \frac{c}{a}a} \right| = c - a.\)
Cho điểm \(M(x;y)\)nằm trên hypebol (H): \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
a) Chứng minh rằng \({F_1}{M^2} - {F_2}{M^2} = 4cx\)
b) Giả sử điểm \(M(x;y)\) thuộc nhánh đi qua \({A_1}( - a;0)\) (Hình 5a). Sử dụng kết quả đã chứng minh được ở câu a) kết hợp với tính chất \(M{F_2} - M{F_1} = 2a\) đã biết để chứng minh \(M{F_2} + M{F_1} = - 2\frac{{cx}}{a}\). Từ đó, chứng minh các công thức: \(M{F_1} = - a - \frac{c}{a}{x_0};M{F_2} = a - \frac{c}{a}{x_0}\)
b) Giả sử điểm \(M(x;y)\) thuộc nhánh đi qua \({A_2}(a;0)\) (Hình 5b). Sử dụng kết quả đã chứng minh được ở câu a) kết hợp với tính chất \(M{F_1} - M{F_2} = 2a\) đã biết để chứng minh \(M{F_2} + M{F_1} = 2\frac{{cx}}{a}\). Từ đó, chứng minh các công thức: \(M{F_1} = a + \frac{c}{a}{x_0};M{F_2} = - a + \frac{c}{a}{x_0}\)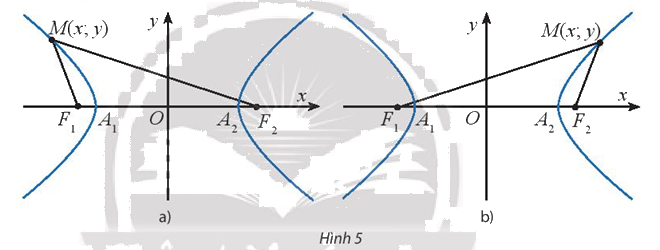
Lời giải chi tiết:
a) Tính \(M{F_1}^2 - M{F_2}^2\)
Ta có: \(\overrightarrow {F{M_1}} (x + c;y);\overrightarrow {{F_2}M} (x - c;y)\)
\( \Rightarrow {F_1}{M^2} = {(x + c)^2} + {y^2};M{F_2}^2 = {(x - c)^2} + {y^2}\)
\( \Rightarrow {F_1}{M^2} - {F_2}{M^2} = {(x + c)^2} - {(x - c)^2} = 4c{x_0}\)
b) Khi điểm \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_1}( - a;0)\) (\(M{F_2} - M{F_1} = 2a\)),
\(\begin{array}{l}M{F_1} + M{F_2} = \frac{{M{F_1}^2 - M{F_2}^2}}{{M{F_1} - M{F_2}}} = - \frac{{2c}}{a}x\\M{F_1} = \frac{{\left( { - \frac{{2c}}{a}x} \right) - 2a}}{2} = - a - \frac{c}{a}x\\M{F_2} = \frac{{\left( { - \frac{{2c}}{a}x} \right) + 2a}}{2} = a - \frac{c}{a}x\end{array}\)
c) Khi điểm \(M(x;y)\) thuộc nhánh chứa đỉnh \({A_2}(a;0)\) (\(M{F_1} - M{F_2} = 2a\)),
\(\begin{array}{l}M{F_1} + M{F_2} = \frac{{M{F_1}^2 - M{F_2}^2}}{{M{F_1} - M{F_2}}} = \frac{{2c}}{a}x\\M{F_1} = \frac{{\frac{{2c}}{a}x + 2a}}{2} = a + \frac{c}{a}x\\M{F_2} = \frac{{\frac{{2c}}{a}x - 2a}}{2} = - a + \frac{c}{a}x\end{array}\)
Cho điểm \(M(x;y)\)nằm trên hypebol (H): \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
a) Chứng minh rằng \({F_1}{M^2} - {F_2}{M^2} = 4cx\)
b) Giả sử điểm \(M(x;y)\) thuộc nhánh đi qua \({A_1}( - a;0)\) (Hình 5a). Sử dụng kết quả đã chứng minh được ở câu a) kết hợp với tính chất \(M{F_2} - M{F_1} = 2a\) đã biết để chứng minh \(M{F_2} + M{F_1} = - 2\frac{{cx}}{a}\). Từ đó, chứng minh các công thức: \(M{F_1} = - a - \frac{c}{a}{x_0};M{F_2} = a - \frac{c}{a}{x_0}\)
b) Giả sử điểm \(M(x;y)\) thuộc nhánh đi qua \({A_2}(a;0)\) (Hình 5b). Sử dụng kết quả đã chứng minh được ở câu a) kết hợp với tính chất \(M{F_1} - M{F_2} = 2a\) đã biết để chứng minh \(M{F_2} + M{F_1} = 2\frac{{cx}}{a}\). Từ đó, chứng minh các công thức: \(M{F_1} = a + \frac{c}{a}{x_0};M{F_2} = - a + \frac{c}{a}{x_0}\)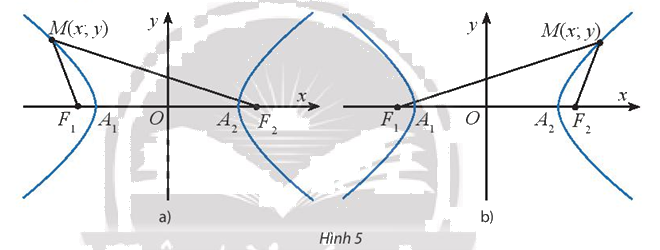
Lời giải chi tiết:
a) Tính \(M{F_1}^2 - M{F_2}^2\)
Ta có: \(\overrightarrow {F{M_1}} (x + c;y);\overrightarrow {{F_2}M} (x - c;y)\)
\( \Rightarrow {F_1}{M^2} = {(x + c)^2} + {y^2};M{F_2}^2 = {(x - c)^2} + {y^2}\)
\( \Rightarrow {F_1}{M^2} - {F_2}{M^2} = {(x + c)^2} - {(x - c)^2} = 4c{x_0}\)
b) Khi điểm \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_1}( - a;0)\) (\(M{F_2} - M{F_1} = 2a\)),
\(\begin{array}{l}M{F_1} + M{F_2} = \frac{{M{F_1}^2 - M{F_2}^2}}{{M{F_1} - M{F_2}}} = - \frac{{2c}}{a}x\\M{F_1} = \frac{{\left( { - \frac{{2c}}{a}x} \right) - 2a}}{2} = - a - \frac{c}{a}x\\M{F_2} = \frac{{\left( { - \frac{{2c}}{a}x} \right) + 2a}}{2} = a - \frac{c}{a}x\end{array}\)
c) Khi điểm \(M(x;y)\) thuộc nhánh chứa đỉnh \({A_2}(a;0)\) (\(M{F_1} - M{F_2} = 2a\)),
\(\begin{array}{l}M{F_1} + M{F_2} = \frac{{M{F_1}^2 - M{F_2}^2}}{{M{F_1} - M{F_2}}} = \frac{{2c}}{a}x\\M{F_1} = \frac{{\frac{{2c}}{a}x + 2a}}{2} = a + \frac{c}{a}x\\M{F_2} = \frac{{\frac{{2c}}{a}x - 2a}}{2} = - a + \frac{c}{a}x\end{array}\)
Tính độ dài hai bán kính qua tiêu của điểm \(M(x;y)\) trên hypebol (H): \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\)
Phương pháp giải:
Cho điểm \(M(x;y)\)nằm trên hypebol (H): \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
Độ dài hai bán kính qua tiêu của điểm \(M(x;y)\) là:
\(M{F_1} = \left| {a + \frac{c}{a}x} \right|;M{F_2} = \left| {a - \frac{c}{a}x} \right|\)
Lời giải chi tiết:
Hypebol (H): \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\) có \(a = 8,b = 6\) suy ra \(c = \sqrt {{a^2} + {b^2}} = 10\).
Độ dài hai bán kính qua tiêu của điểm \(M(x;y)\) là:
\(M{F_1} = \left| {a + \frac{c}{a}x} \right| = \left| {8 + \frac{3}{4}x} \right|;M{F_2} = \left| {a - \frac{c}{a}x} \right| = \left| {8 - \frac{3}{4}x} \right|\)
Tính độ dài hai bán kính qua tiêu của đỉnh \({A_2}(a;0)\) trên hypebol (H): \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
Phương pháp giải:
Cho điểm \(M(x;y)\)nằm trên hypebol (H): \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
Độ dài hai bán kính qua tiêu của điểm \(M(x;y)\) là:
\(M{F_1} = \left| {a + \frac{c}{a}x} \right|;M{F_2} = \left| {a - \frac{c}{a}x} \right|\)
Lời giải chi tiết:
Độ dài hai bán kính qua tiêu của điểm \({A_2}(a;0)\) trên (H) là:
\(M{F_1} = \left| {a + \frac{c}{a}x} \right| = \left| {a + \frac{c}{a}a} \right| = a + c;M{F_2} = \left| {a - \frac{c}{a}x} \right| = \left| {a - \frac{c}{a}a} \right| = c - a.\)
Mục 2 của Chuyên đề học tập Toán 10 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình. Việc nắm vững kiến thức nền tảng và phương pháp giải bài tập là yếu tố then chốt để đạt kết quả tốt. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 2 trang 52, 53, đồng thời phân tích các khái niệm quan trọng và kỹ năng cần thiết.
Bài tập này yêu cầu… (mô tả bài tập). Để giải bài tập này, chúng ta cần áp dụng kiến thức về… (liệt kê kiến thức liên quan). Các bước giải như sau:
Kết luận: … (kết quả cuối cùng và giải thích).
Bài tập này yêu cầu… (mô tả bài tập). Đây là một bài tập ứng dụng thực tế, đòi hỏi học sinh phải…
Lời giải chi tiết:
… (giải thích chi tiết từng bước giải)
Bài tập này thuộc dạng… (phân loại bài tập). Để giải quyết bài toán này, chúng ta cần…
| Bước | Thực hiện | Giải thích |
|---|---|---|
| 1 | … | … |
| 2 | … | … |
Để giải quyết các bài tập trong mục 2 trang 52, 53, học sinh cần nắm vững các khái niệm sau:
Dưới đây là một số mẹo và lưu ý giúp bạn giải bài tập hiệu quả hơn:
Kiến thức trong mục 2 trang 52, 53 có ứng dụng rộng rãi trong thực tế, ví dụ như…
Hy vọng rằng với lời giải chi tiết và những phân tích trên, bạn đã hiểu rõ hơn về cách giải các bài tập trong mục 2 trang 52, 53 Chuyên đề học tập Toán 10 - Chân trời sáng tạo. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.