Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 15, 16, 17 Chuyên đề học tập Toán 10 - Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập.
Bài giải này được xây dựng bởi đội ngũ giáo viên giàu kinh nghiệm, đảm bảo tính chính xác và phù hợp với chương trình học.
Một nhà hóa học có ba dung dịch cùng một loại acid nhưng với nồng độ khác nhau là 10%, 20% và 40%. Trong một thí nghiệm,
Một nhà hóa học có ba dung dịch cùng một loại acid nhưng với nồng độ khác nhau là 10%, 20% và 40%. Trong một thí nghiệm, để tạo ra 100ml dung dịch nồng độ 18%, nhà hóa học đã sử dụng lượng dung dịch nồng độ 10% gấp bốn lần lượng dung dịch nồng độ 40%. Tính số mililit dung dịch mỗi loại mà nhà hóa học đó đã sử dụng trong thí nghiệm này.
Phương pháp giải:
Bước 1: Lập hệ phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết
+ Lập các phương trình biểu thị mối quan hệ giữa các đại lượng
Bước 2: Giải hệ phương trình
Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
Lời giải chi tiết:
Gọi số mililit dung dịch mỗi loại 10%, 20% và 40% sử dụng trong thí nghiệm là x, y, z (đơn vị mililit) \((x,y,z > 0)\)
Tạo ra 100ml dung dịch mới nên ta có: \(x + y + z = 100\)
Khối lượng chất tan trong dung dịch mới là: \(10\% x + 20\% y + 40\% z = 18\% .100 \Leftrightarrow 0,1x + 0,2y + 0,4z = 18\)
Lượng dung dịch nồng độ 10% gấp bốn lần lượng dung dịch nồng độ 40% nên \(x = 4z\)
Từ đó ta có hệ phương trình bậc nhất ba ẩn:
\(\left\{ \begin{array}{l}x + y + z = 100\\0,1x + 0,2y + 0,4z = 18\\x - 4z = 0\end{array} \right.\)
Sử dụng máy tính cầm tay, ta được \(x = 40;y = 50;z = 10\)
Vậy nhà hóa học đó đã dùng 40ml dung dịch 10%, 50ml dung dịch 20%,10ml dung dịch 40%.
Ba loại tế bào A, B, C thực hiện số lần nguyên phân lần lượt là 3, 4, 7 và tổng số tế bào con tạo ra là 480. Biết rằng khi chưa thực hiện nguyên phân, số tế bào loại B bằng tổng số tế bào loại A và loại C. Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại C được tạo ra gấp năm lần số tế bào con loại B được tạo ra. Tính số tế bào con mỗi loại lúc ban đầu.
Phương pháp giải:
Bước 1: Lập hệ phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết
+ Lập các phương trình biểu thị mối quan hệ giữa các đại lượng
Bước 2: Giải hệ phương trình
Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
Lời giải chi tiết:
Gọi số tế bào con mỗi loại A, B, C lúc đầu là x, y, z (tế bào) \((x,y,z \in \mathbb{N})\)
Tổng số tế bào con tạo ra là 480 tế bào nên \(x{.2^3} + y{.2^4} + z{.2^7} = 480\)
Khi chưa thực hiện nguyên phân, số tế bào loại B bằng tổng số tế bào loại A và loại C nên \(y = x + z\)
Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại C được tạo ra gấp năm lần số tế bào con loại B được tạo ra nên \(x{.2^3} + z{.2^7} = 5y{.2^4}\)
Từ đó ta có hệ phương trình bậc nhất ba ẩn:
\(\left\{ \begin{array}{l}x{.2^3} + y{.2^4} + z{.2^7} = 480\\y = x + z\\x{.2^3} + z{.2^7} = 5y{.2^4}\end{array} \right.\)
Sử dụng máy tính cầm tay, ta được \(x = 2;y = 5;z = 3\)
Vậy ban đầu có 2 tế bào loại A, 5 tế bào loại B và 3 tế bào loại C.
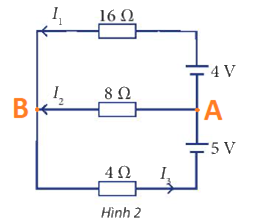
Cho sơ đồ mạch điện như Hình 2. Tính các cường độ dòng điện \({I_1},{I_2},{I_3}\)
Phương pháp giải:
Bước 1: Lập hệ phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết
+ Lập các phương trình biểu thị mối quan hệ giữa các đại lượng
Bước 2: Giải hệ phương trình
Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
Lời giải chi tiết:
Ta có:
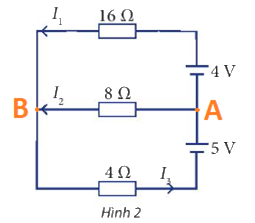
\(\left. \begin{array}{l}{U_{AB}} = - {E_1} + {I_1}{R_1} = - 4 + 16{I_1}\\{U_{AB}} = {I_2}{R_2} = 8{I_2}\\{U_{AB}} = {E_2} - {I_3}{R_3} = 5 - 4{I_3}\end{array} \right\} \Rightarrow \left\{ \begin{array}{l} - 4 + 16{I_1} = 8{I_2}\\5 - 4{I_3} = 8{I_2}\end{array} \right.\)
Tại nút B: \({I_1} + {I_2} = {I_3}\)
Từ đó ta có hệ phương trình bậc nhất ba ẩn:
\(\left\{ \begin{array}{l}16{I_1} - 8{I_2} = 4\\8{I_2} + 4{I_3} = 5\\{I_1} + {I_2} - {I_3} = 0\end{array} \right.\)
Sử dụng máy tính cầm tay, ta được \({I_1} = \frac{{11}}{{28}},{I_2} = \frac{2}{7},{I_3} = \frac{{19}}{{28}}\)
Vậy \({I_1} = \frac{{11}}{{28}}A,{I_2} = \frac{2}{7}A,{I_3} = \frac{{19}}{{28}}A\)
Một nhà hóa học có ba dung dịch cùng một loại acid nhưng với nồng độ khác nhau là 10%, 20% và 40%. Trong một thí nghiệm, để tạo ra 100ml dung dịch nồng độ 18%, nhà hóa học đã sử dụng lượng dung dịch nồng độ 10% gấp bốn lần lượng dung dịch nồng độ 40%. Tính số mililit dung dịch mỗi loại mà nhà hóa học đó đã sử dụng trong thí nghiệm này.
Phương pháp giải:
Bước 1: Lập hệ phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết
+ Lập các phương trình biểu thị mối quan hệ giữa các đại lượng
Bước 2: Giải hệ phương trình
Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
Lời giải chi tiết:
Gọi số mililit dung dịch mỗi loại 10%, 20% và 40% sử dụng trong thí nghiệm là x, y, z (đơn vị mililit) \((x,y,z > 0)\)
Tạo ra 100ml dung dịch mới nên ta có: \(x + y + z = 100\)
Khối lượng chất tan trong dung dịch mới là: \(10\% x + 20\% y + 40\% z = 18\% .100 \Leftrightarrow 0,1x + 0,2y + 0,4z = 18\)
Lượng dung dịch nồng độ 10% gấp bốn lần lượng dung dịch nồng độ 40% nên \(x = 4z\)
Từ đó ta có hệ phương trình bậc nhất ba ẩn:
\(\left\{ \begin{array}{l}x + y + z = 100\\0,1x + 0,2y + 0,4z = 18\\x - 4z = 0\end{array} \right.\)
Sử dụng máy tính cầm tay, ta được \(x = 40;y = 50;z = 10\)
Vậy nhà hóa học đó đã dùng 40ml dung dịch 10%, 50ml dung dịch 20%,10ml dung dịch 40%.
Ba loại tế bào A, B, C thực hiện số lần nguyên phân lần lượt là 3, 4, 7 và tổng số tế bào con tạo ra là 480. Biết rằng khi chưa thực hiện nguyên phân, số tế bào loại B bằng tổng số tế bào loại A và loại C. Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại C được tạo ra gấp năm lần số tế bào con loại B được tạo ra. Tính số tế bào con mỗi loại lúc ban đầu.
Phương pháp giải:
Bước 1: Lập hệ phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết
+ Lập các phương trình biểu thị mối quan hệ giữa các đại lượng
Bước 2: Giải hệ phương trình
Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
Lời giải chi tiết:
Gọi số tế bào con mỗi loại A, B, C lúc đầu là x, y, z (tế bào) \((x,y,z \in \mathbb{N})\)
Tổng số tế bào con tạo ra là 480 tế bào nên \(x{.2^3} + y{.2^4} + z{.2^7} = 480\)
Khi chưa thực hiện nguyên phân, số tế bào loại B bằng tổng số tế bào loại A và loại C nên \(y = x + z\)
Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại C được tạo ra gấp năm lần số tế bào con loại B được tạo ra nên \(x{.2^3} + z{.2^7} = 5y{.2^4}\)
Từ đó ta có hệ phương trình bậc nhất ba ẩn:
\(\left\{ \begin{array}{l}x{.2^3} + y{.2^4} + z{.2^7} = 480\\y = x + z\\x{.2^3} + z{.2^7} = 5y{.2^4}\end{array} \right.\)
Sử dụng máy tính cầm tay, ta được \(x = 2;y = 5;z = 3\)
Vậy ban đầu có 2 tế bào loại A, 5 tế bào loại B và 3 tế bào loại C.
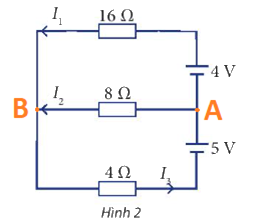
Cho sơ đồ mạch điện như Hình 2. Tính các cường độ dòng điện \({I_1},{I_2},{I_3}\)
Phương pháp giải:
Bước 1: Lập hệ phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết
+ Lập các phương trình biểu thị mối quan hệ giữa các đại lượng
Bước 2: Giải hệ phương trình
Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
Lời giải chi tiết:
Ta có:
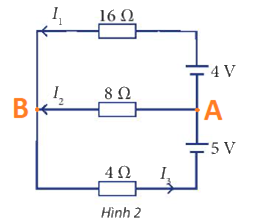
\(\left. \begin{array}{l}{U_{AB}} = - {E_1} + {I_1}{R_1} = - 4 + 16{I_1}\\{U_{AB}} = {I_2}{R_2} = 8{I_2}\\{U_{AB}} = {E_2} - {I_3}{R_3} = 5 - 4{I_3}\end{array} \right\} \Rightarrow \left\{ \begin{array}{l} - 4 + 16{I_1} = 8{I_2}\\5 - 4{I_3} = 8{I_2}\end{array} \right.\)
Tại nút B: \({I_1} + {I_2} = {I_3}\)
Từ đó ta có hệ phương trình bậc nhất ba ẩn:
\(\left\{ \begin{array}{l}16{I_1} - 8{I_2} = 4\\8{I_2} + 4{I_3} = 5\\{I_1} + {I_2} - {I_3} = 0\end{array} \right.\)
Sử dụng máy tính cầm tay, ta được \({I_1} = \frac{{11}}{{28}},{I_2} = \frac{2}{7},{I_3} = \frac{{19}}{{28}}\)
Vậy \({I_1} = \frac{{11}}{{28}}A,{I_2} = \frac{2}{7}A,{I_3} = \frac{{19}}{{28}}A\)
Mục 2 của Chuyên đề học tập Toán 10 - Chân trời sáng tạo tập trung vào các khái niệm và bài tập liên quan đến vectơ. Đây là một phần quan trọng trong chương trình học, đặt nền móng cho các kiến thức hình học nâng cao hơn. Việc nắm vững các định nghĩa, tính chất và ứng dụng của vectơ là điều cần thiết để giải quyết các bài toán một cách hiệu quả.
Bài tập này yêu cầu học sinh biểu diễn các vectơ dựa trên các điểm cho trước. Để giải bài này, học sinh cần hiểu rõ cách xác định vectơ bằng tọa độ và cách thực hiện các phép toán cộng, trừ vectơ.
Bài tập này tập trung vào các phép toán cộng, trừ vectơ, nhân vectơ với một số thực. Học sinh cần nắm vững các quy tắc thực hiện các phép toán này để đảm bảo tính chính xác của kết quả.
Bài tập này yêu cầu học sinh sử dụng kiến thức về vectơ để giải quyết các bài toán hình học, chẳng hạn như chứng minh hai đường thẳng song song, tìm tọa độ trung điểm của đoạn thẳng, tính độ dài đoạn thẳng.
Ví dụ: Cho A(1; 2), B(3; 4) và C(5; 6). Chứng minh A, B, C thẳng hàng.
Giải: Tính vectơ AB và AC. Nếu hai vectơ này cùng phương thì A, B, C thẳng hàng.
| Vectơ | Tọa độ |
|---|---|
| AB | (2; 2) |
| AC | (4; 4) |
Vì AC = 2AB nên hai vectơ này cùng phương, do đó A, B, C thẳng hàng.
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức về vectơ:
Việc giải các bài tập trong mục 2 trang 15, 16, 17 Chuyên đề học tập Toán 10 - Chân trời sáng tạo là một bước quan trọng trong quá trình học tập môn Toán. Hy vọng rằng với bài giải chi tiết và các lưu ý trên, các em học sinh sẽ tự tin hơn khi đối mặt với các bài toán về vectơ. Chúc các em học tốt!